Cost Function and Backpropagation
Cost Function
在求取神经网络权重矩阵时,第一步也是要先写出cost function。它的cost function就是带rugularization
的logistic regression的加强版,因为在多种类分类中每个数据不再只有一个输出y(i),而是有K个0/1输出组
成一个向量(K为种类数),因此神经网络的cost function为:
注意后面的regularization部分仍然不计算bias unit(θ0)
Cost Function and Backpropagation
同样,在做gradient descent时需要先知道J(θ)以及每个参数关于J(θ)的偏导数,包括每层的权重矩阵(L)
中的每个元素(i,j),是个3重循环。
用δl,j表示第l层第j节点对最终结果的残差有多少影响。首先最后一层很好计算,使用δ(last) = a(last) - y即
可。计算隐藏层的δ可以使用以下公式:
!上图有错误:g’(z) = g(z) * (1 - g(z))
证明可以看这里:http://blog.csdn.net/abcjennifer/article/details/7758797
需要记住的就是J(θ)关于权重参数Θ(l,i,j)的偏导数就是a(l,j),*δ(l+1,.i)。注意不需要求δ(1),因为第一层是输
入层,不需要修改。
整体的back propagation算法如下图所视:
注意for i = 1 to m中的i和下面的i没有关系,这里有歧义。
上述矩阵中,a(i)(除最后一层外),D是包含bias unit的,z和δ是不包含bias unit的。
最后计算出的D矩阵就是所要的偏导数矩阵。
Backpropagation in Practice
Implementation Note: Unrolling Parameter
fminunc的语法为:
optTheta = fminunc(@(t)costfunction(t, X, y, lambda), initial_theta, options)
[ J, grad ] = costfunction(theta, X, y, lambda)
在logistic regression中,grad,initial_theta,theta都是向量,而到了神经网络中这些都变成了矩阵,这
里讲一种方法把这些矩阵转换为向量。在octave中使用A = A(:)就可以把一个矩阵转换成列向量,使用A =
reshape(A, (m,n))就可以把A还原回m*n矩阵。
因此,[ J, gradVec ] = costfunction(thetaVec, X, y, lambda) 的过程为:
1.reshape thetaVec 得到初始权重矩阵
2.通过forward/backward propagation得到偏导数矩阵D
3.把D转换成向量gradVec返回
Gradient Checking
在编写backward propagation时有可能出现bug,即使看起来J(θ)确实在递减,其中也可能隐含着错误。本
节介绍一种方法来确定所求的偏导矩阵是否正确。
一种估计J(θ)在θ点导数的方法:
取e为极小值(通常10^-4),连接J(θ-e)和J(θ+e)两点,认为该直线的斜率就是在θ点的导数。
当θ包含多个参数时依然可以使用这种方法:
最后检查这个估计值是否约等于求出的偏导矩阵D
Random Initialization
theta的初始值不能随便取,如果全取0的话,不仅每个ai,j会相等,它们关于J(θ)的偏导数也相等,因此
每一层的theta值依然会保持相等。为了解决这个问题,对于theta的初值要随机初始化为[-ε,ε]之间的随机
数。
使用Theta = rand(m,n) * (2*ε) - ε。 其中rand()生成(-1,1)之间的数。
Putting It Together
在构造神经网络时,一般来说每个隐藏层的节点数量最好相同,而且多于输入层节点数量,通常是数量越多
效果越好。
总的步骤为:
1.随机初始化权重矩阵
2.对于每个数据x(i),使用forward propagation计算hθ(x(i))
3.使用hθ(x(i))计算J(θ)
4.使用backward propagation计算偏导数矩阵D
5.使用Gradient Check对D矩阵进行检查
6.使用gradient descent+backward propagation求出最佳权重矩阵
尽管J(θ)是non-convex的,gradient descent等算法一般会找到一个非常优的局部最优解(尽管可能不是全
局最优解)。
Application of Neural Networks
Autonomous Driving
本节介绍了一个神经网络的应用:自动驾驶,原理是把一个人在一段时间内的驾驶操作序列作为训练集,每
秒钟20次用照相机记录车前方道路情况,及此时驾驶员做的驾驶操作。接下来就是用神经网络进行决策了。








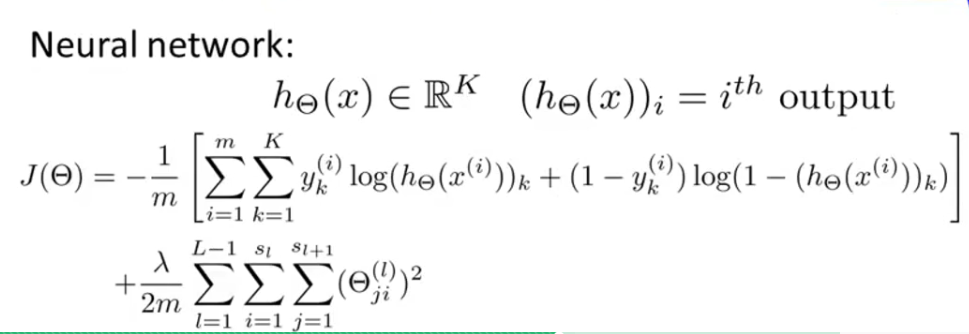
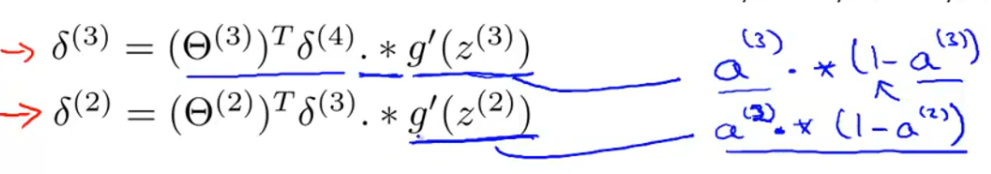

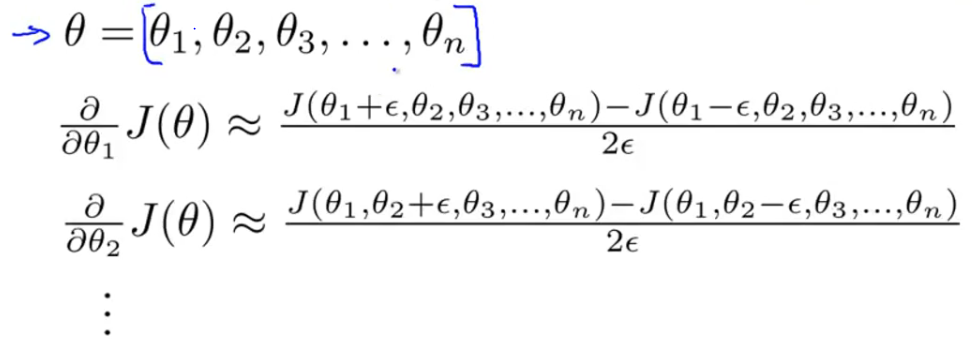
















 818
818

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








