用Python绘制超炫酷动态莫比乌斯环：数学与编程的完美结合

编程不良人1

已于 2025-05-11 20:41:05 修改

阅读量706

点赞数 27

文章标签： python 开发语言

于 2025-05-11 20:16:33 首次发布

本文链接：https://blog.csdn.net/Bejpse/article/details/147877292

版权

本文将带您用Python代码实现一个令人惊艳的动态莫比乌斯环，结合三维可视化与动画效果，展现数学之美与编程魔法的碰撞。通过参数方程实现空间扭曲，运用Matplotlib打造流动的渐变色与视角旋转效果，最终呈现出一个仿佛来自异次元的动态曲面。（效果图见文末）

一、效果预览

最终实现效果：

动态背景：背景颜色随时间变化，呈现出动态的渐变效果。
动态透明度：莫比乌斯带的透明度随时间波动，增加了视觉层次感。
动态颜色映射：颜色映射随时间变化，增强了动画的炫酷效果。
动态视角：视角不断旋转，增加了动画的动态感。

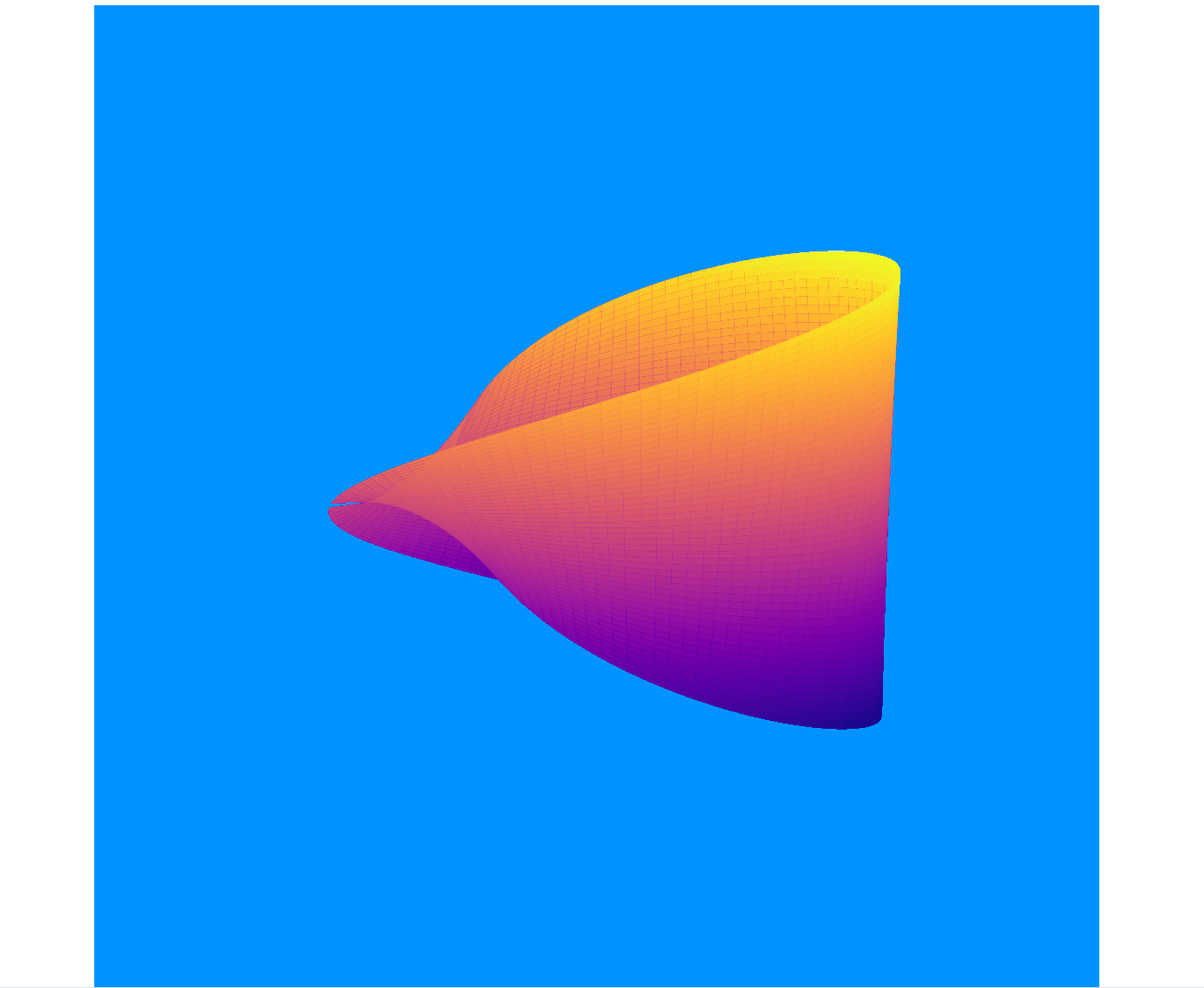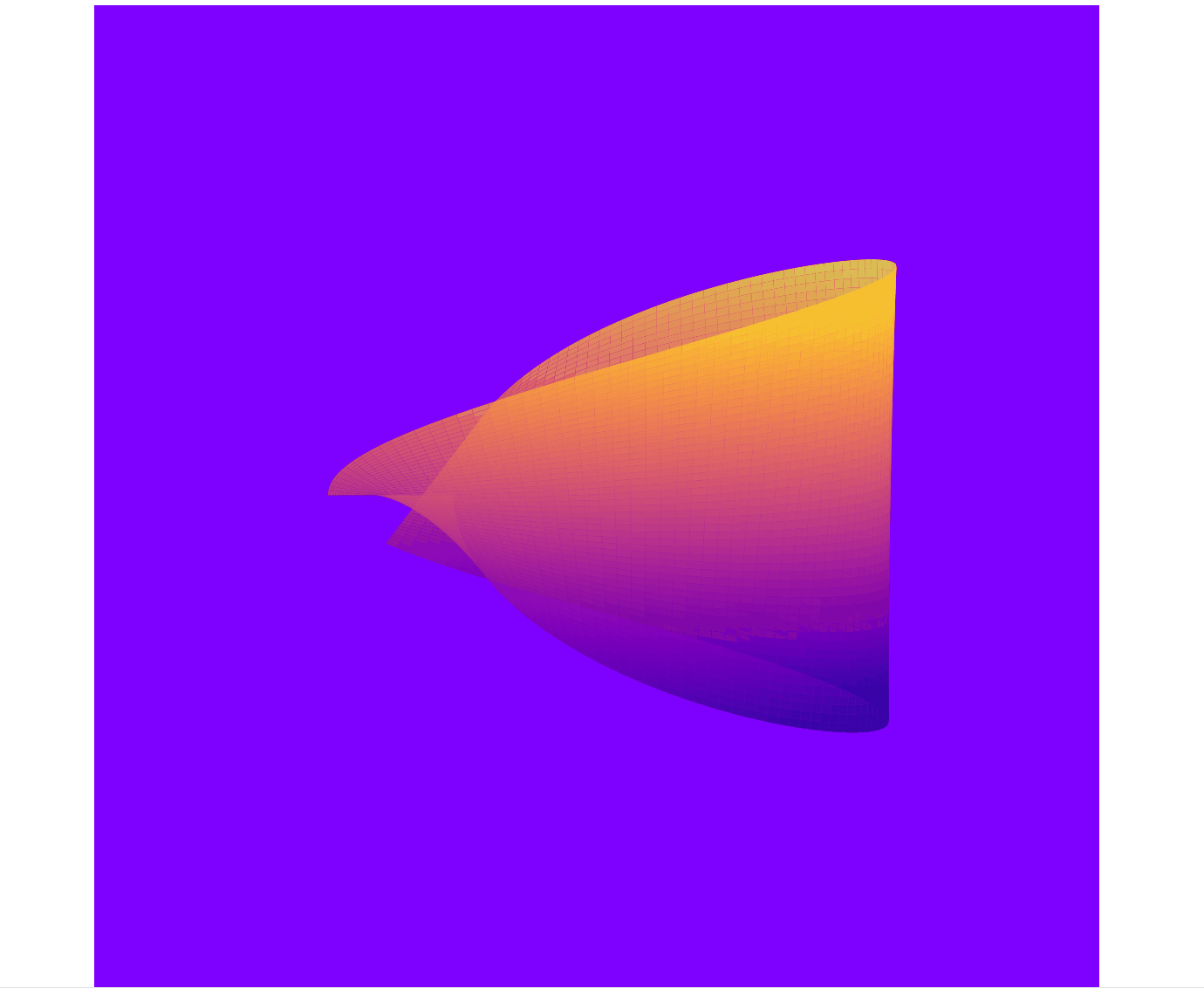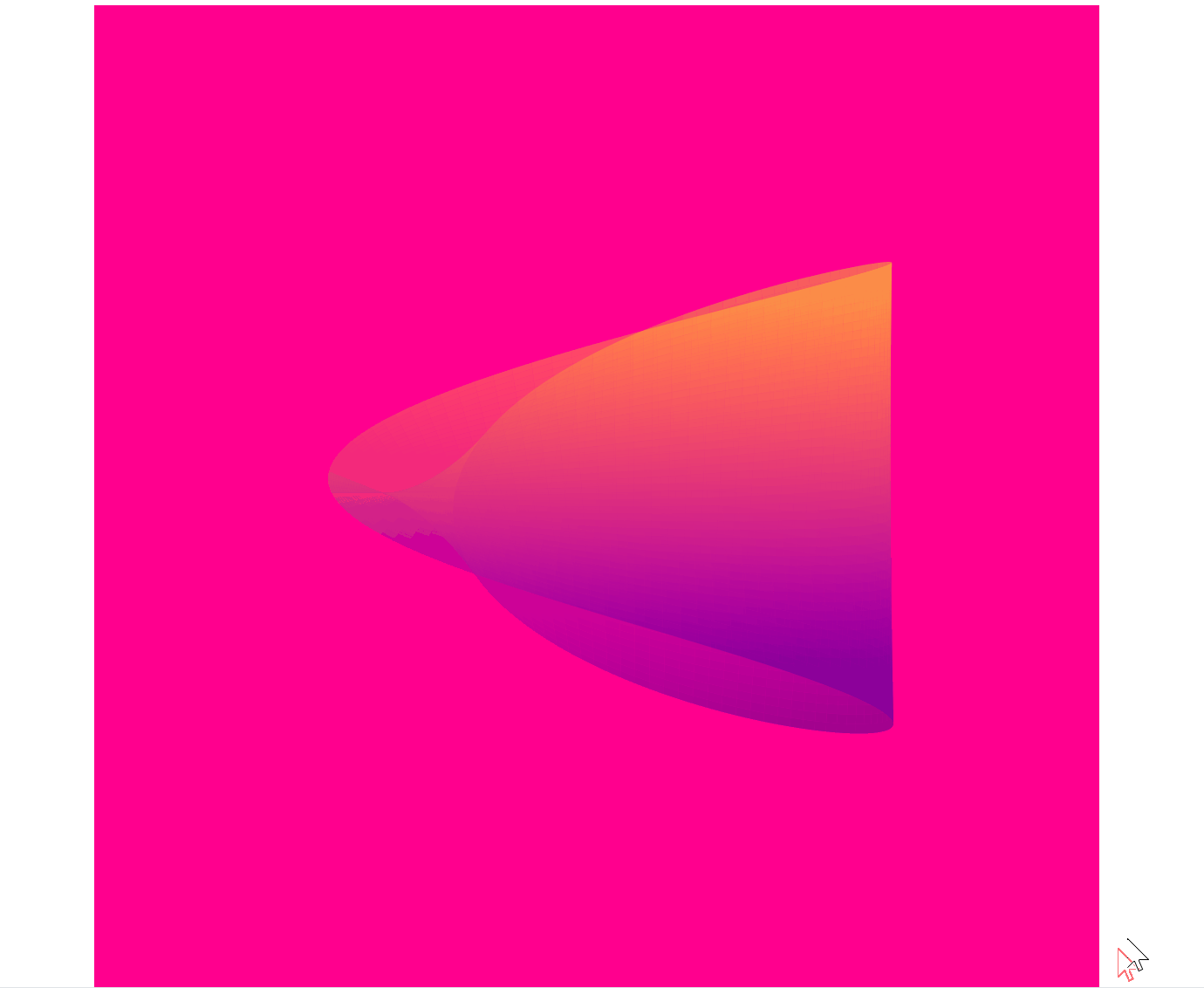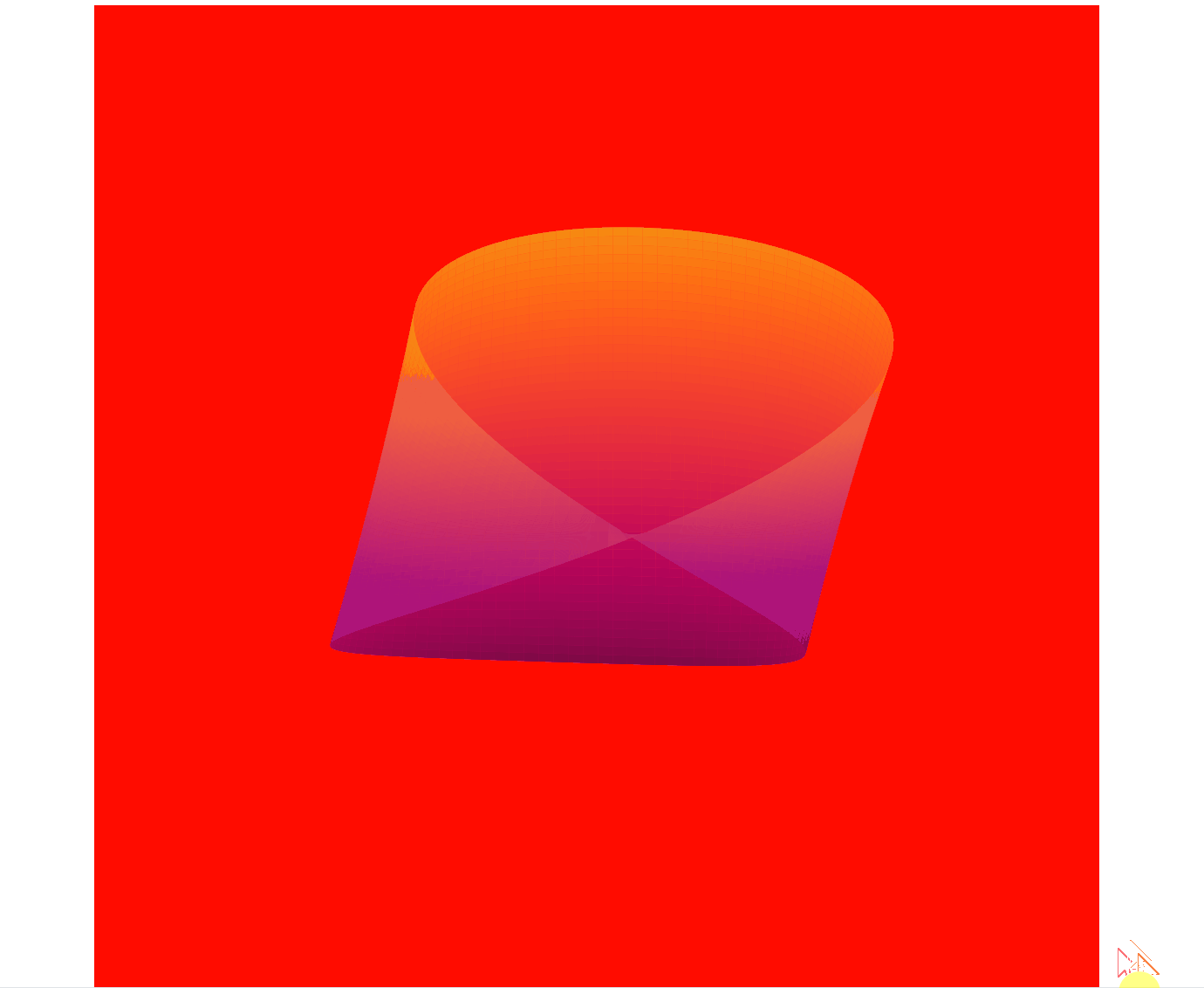
二、数学原理与参数方程

2.1 莫比乌斯带特性

莫比乌斯带不仅是数学史上的经典发现，更是理解非定向曲面的关键模型。其独特性质源于不可定向性的拓扑特征：

单侧性证明实验：用毛笔沿着表面中心线连续涂抹，最终将覆盖整个表面
边界等价性：将普通环带边界切开得到两个独立圆，而莫比乌斯带切开后仍保持单一边界
手性特征：存在左旋与右旋两种不可重合的拓扑形态

2.2 莫比乌斯带的数学原理

莫比乌斯带是一种只有一个面的几何结构，具有独特的数学性质。它的参数方程如下：

( x = (R + v \cdot \cos(u/2)) \cdot \cos(u) )
( y = (R + v \cdot \cos(u/2)) \cdot \sin(u) )
( z = v \cdot \sin(u/2) )

其中：

( u ) 是角度参数，控制莫比乌斯带的环绕。
( v ) 是宽度参数，控制莫比乌斯带的带宽。
( R ) 是主要半径，决定莫比乌斯带的整体大小。

在动画中，我们通过时间参数 ( t ) 动态调整 ( u )，使莫比乌斯带的形状随时间发生轻微变化。

2.3 参数方程解析

def mobius(u, v, t=0):
    R = 2  # 主半径
    w = 1  # 带宽
    u = u * (1 + 0.1 * np.sin(t))  # 动态形变
    x = (R + v * np.cos(u/2)) * np.cos(u)
    y = (R + v * np.cos(u/2)) * np.sin(u)
    z = v * np.sin(u/2)
    return x, y, z

参数说明：

u ∈ [0, 2π]：环绕角度
v ∈ [-0.5, 0.5]：带宽参数
t：时间变量（用于动画）
关键构造：u/2 实现180度扭转

三、代码实现详解

3.1 环境配置

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from mpl_toolkits.mplot3d import Axes3D

3.2 可视化配置技巧

# 初始化画布
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')

# 隐藏坐标轴和网格
ax.set_facecolor('black')
ax.grid(False)
ax.set_axis_off()

3.3 动画引擎核心

def update(frame):
    # 清空画布
    ax.cla()
    
    # 动态背景（HSV色相循环）
    bg_color = plt.cm.hsv((frame % 100) / 100)
    ax.set_facecolor(bg_color)
    
    # 生成动态曲面
    X, Y, Z = mobius(U, V, frame / 10)
    
    # 透明度波动效果
    alpha = 0.5 + 0.5 * np.sin(frame / 20)
    
    # 绘制曲面
    surf = ax.plot_surface(X, Y, Z, 
                          rstride=1, cstride=1,
                          cmap='plasma',        # 等离子色系
                          alpha=alpha,          # 动态透明度
                          edgecolor='none',     # 隐藏边线
                          antialiased=True)
    
    # 自动旋转视角
    ax.view_init(elev=10 + 10 * np.sin(frame / 50), 
                 azim=frame * 0.5)
    
    return surf,

3.4 启动动画

ani = FuncAnimation(fig, update, 
                   frames=200,  # 总帧数
                   interval=50, # 帧间隔(ms)
                   blit=False)

plt.show()

3.5 完整代码

import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from mpl_toolkits.mplot3d import Axes3D

# 莫比乌斯带参数方程
def mobius(u, v, t=0):
    R = 2  # 主要半径
    w = 1  # 带宽
    u = u * (1 + 0.1 * np.sin(t))  # 添加动态形变（可选）
    x = (R + v * np.cos(u/2)) * np.cos(u)
    y = (R + v * np.cos(u/2)) * np.sin(u)
    z = v * np.sin(u/2)
    return x, y, z

# 初始化图形
fig = plt.figure(figsize=(8, 8))
ax = fig.add_subplot(111, projection='3d')
ax.set_facecolor('black')
ax.grid(False)
ax.set_axis_off()

# 生成参数网格
u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(-0.5, 0.5, 50)
U, V = np.meshgrid(u, v)

# 动画更新函数
def update(frame):
    ax.cla()
    
    # 动态背景颜色
    bg_color = plt.cm.hsv((frame % 100) / 100)  # 背景颜色随时间变化
    ax.set_facecolor(bg_color)
    ax.grid(False)
    ax.set_axis_off()
    
    # 添加时间参数生成动态效果
    X, Y, Z = mobius(U, V, frame / 10)
    
    # 动态透明度和颜色映射
    alpha = 0.5 + 0.5 * np.sin(frame / 20)  # 透明度随时间波动
    cmap = plt.cm.hsv((frame % 100) / 100)  # 动态颜色映射
    surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='plasma', 
                           alpha=alpha, edgecolor='none', antialiased=True)
    
    # 添加旋转视角
    ax.view_init(elev=10 + 10 * np.sin(frame / 50), azim=frame * 0.5)
    
    return surf,

# 创建动画
ani = FuncAnimation(fig, update, frames=200, interval=50, blit=False)

# 显示动画
plt.show()

四、关键效果优化

4.1 动态形变增强

修改参数方程中的形变系数：

u = u * (1 + 0.5 * np.sin(t*2))  # 增强波动幅度

4.2 色彩方案替换

尝试不同的colormap：

cmap='twilight'    # 曙光色
cmap='hsv'         # 彩虹色
cmap='viridis'     # 翡翠色

4.3 性能优化建议

减少网格密度：np.linspace(..., 50)
关闭抗锯齿：antialiased=False
降低帧数：frames=100

五、静态到动态对比

Matplotlib作为Python最著名的可视化库，其三维模块和动画模块是创建科技可视化作品的核心工具。本模块将分静态图像和动画两大方向，解析关键函数与实战技巧。

5.1 静态三维可视化

核心函数一览

函数名称	适用场景	关键参数说明
`plot_surface()`	曲面绘制	`cmap`, `alpha`, `rstride`
`plot_wireframe()`	线框模型	`linewidth`, `color`
`scatter()`	散点云图	`s`, `c`, `marker`
`contour()`	等高线投影	`zdir`, `offset`
`quiver()`	矢量场绘制	`length`, `normalize`

静态莫比乌斯环实现

# 生成静态曲面
U_static = np.linspace(0, 2*np.pi, 100)
V_static = np.linspace(-0.5, 0.5, 50)
U, V = np.meshgrid(U_static, V_static)
X, Y, Z = mobius(U, V)  # 调用参数方程

# 创建画布
fig_static = plt.figure(figsize=(10,6))
ax_static = fig_static.add_subplot(111, projection='3d')

# 绘制双模式视图
ax_static.plot_surface(X, Y, Z, cmap='viridis', alpha=0.8)  # 半透明曲面
ax_static.plot_wireframe(X, Y, Z, color='black', linewidth=0.3)  # 叠加线框

# 视角配置
ax_static.view_init(elev=25, azim=-45)
plt.tight_layout()
plt.show()

高级渲染技巧

材质效果：通过lighting=True开启光照模拟
纹理映射：使用facecolors=texture实现图像贴图
多视图布局：plt.subplot(221)创建四联面板

5.2 动态可视化引擎

动画模块核心架构

graph TD
    A[Figure对象] --> B[FuncAnimation初始化]
    B --> C[帧生成器frames]
    C --> D[update函数]
    D --> E{渲染控制}
    E -->|interval| F[帧间隔控制]
    E -->|blit| G[局部刷新优化]

关键参数解析

class FuncAnimation:
    def __init__(self, fig, func, frames=None, 
                 init_func=None, interval=200, 
                 blit=False, cache_frame_data=True):
        """
        fig : 画布对象
        func : 帧更新函数（需返回可迭代对象）
        frames : 帧序列生成器（支持迭代器/生成器）
        interval : 帧间隔（毫秒）
        blit : 是否启用差异渲染（性能优化）
        """