Algorithm Analysis & Design: Dynamic Programming - Optimal BST

Hi peers,

In this essay, I will introduce a dynamic programming algorithm that can construct an optimal binary search tree. Before we talk about the algorithm, let’s first understand what an optimal BST is.

Concept of Optimal BST
Given a set of values V: {v_1, v_2, …, v_n} stored in the database, people may want to search for a certain value in V from time to time. P: {p_1, p_2, …, p_n} denotes the frequency of a certain value that appears in the search.

Now, we would like to construct a binary search tree to store all values in V to expedite the search. In such a BST, each value resides in a certain level of the tree. d_i denotes the depth of node that stores the value v_i. D: {d_1, d_2, …, d_n} denotes the set that collects the depth for every node in the tree.

Intuitively, we want to construct a tree where the most frequently searched value should be stored “shallowly” (i.e. in a smaller depth). This can significantly minimize the search time if the searching requests scales up. By this intuition, we have the following cost function.

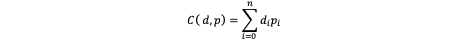
Any binary search tree that can minimize the above cost function is called optimal binary search tree.

A Dynamic Programming Approach
In this section, I will introduce a dynamic programming algorithm that enables us to construct an optimal BST.

• Optimal Substructure
  Lemma1: Every subtree of an optimal BST should be an optimal BST.
  Proof:
  We can prove this lemma by contradiction. Let’s consider an optimal BST T and its subtree T’, which is not an optimal BST. The fact that T’ is not an optimal BST implies that there is another subtree T*, which has a lower cost than T’. By replacing T’ with T*, the cost of T will be lowered. This contradicts the fact that T is an optimal BST. Thus, T’ must be an optimal BST.
  By lemma1, we can derive the cost of an optimal BST from its subtree as follows. In the following, C_i,j denotes the cost of the tree that contains the value {v_i, v_i+1, v_i+2, …, v_j-1, v_j}. C_i, r-1 is the cost of the left subtree, while C_r+1, j is the cost of the right subtree. P_r the frequency of the value that the root node stores.
  Ci,j = C_i, r-1 + p_r + C_r+1, j
  With this equation, we know how we can calculate the cost for our optimal tree, given the information of its optimal left subtree and optimal right subtree.
• Intuition behind the Algorithm
  Our dynamic programming algorithm first considers all possible trees of size 1 (i.e. contains only 1 node) that can be formed from given set V: {v_1, v_2, …, v_n}. Obviously, there are n possibilities of tree of size 1. By choosing every value in the set V in turn to be the root and also the only node in the tree, we can form n different tree of size 1. It is also easy to calculate the cost of these trees. As each of them has only one node, the cost of the entire tree is just the cost of the single node. After we calculate the cost for each possible tree of size 1, we store it in an array for future use.
  Let’s consider one more concrete case – calculating the cost for the optimal tree of size 2. Given the set of values V: {v_1, v¬_2, …, v_n}, we can form n-1 possible trees of size 2. Take one possible example for illustration - a tree of size 2 contains value v_x and v_y. The tree has two possible costs by choosing either v_x or v_y as its root. We calculate and compare these two possible costs. The smaller one will be the cost of the optimal tree. Then, we store it for future reference.
  After the algorithm considers the above two cases, it will consider the optimal tree of size 3, size 4, …. Let’s now consider the possible tree of size k that can be formed from the given set of values V’: {v_j, v_j+1, … v_j+k-1}. Since V’ contains k values, we have k possibilities of roots of the tree of size k to be formed from the set V’. Then, we consider every one of them in turn. Take one possible tree as an example for illustration. If we take v_j+1 as the root of the tree, this tree will have a left subtree of size 1, and a right subtree of size k-2. Remember that we have calculated and stored the cost for optimal tree of size 1 and size k-2 so far. We can simply look up their value. Thus, we can calculate the cost of the tree with root v_j+1 as follows.
  C_j, j+k-1 = C_j,j + p_j+1 + C_j-2, j+k-1
  By repeating the same process with other possible tree of size k, we calculate the costs for every one of them and store the smallest one as the optimal cost for tree of size k.
  Till this point, I guess you have a good understanding on how the algorithm will proceed. With the above process, we can expect the algorithm to give us the cost of the optimal tree of size n at the end. In the following section, we will give the

PseudoCodes

Initialize a 2D Array[n+1][n+1];
Initialize an array V[n+1] for storing given values; 
Initialize an array P[n+1] for storing given frequencies; 

//calculate the optimal cost of tree of size 1 
For k = 0 to n: 
A[k][k] = 1*P[k]. 

For i = 2 to n: 
//i: size of the tree; starting at size 2 because we already processed tree of size 1 above
	for j = 0 to n:
	// j represents the index of the smallest values in the tree
		MinCost  = +∞;
		For t = j to i+j-1: 
			Cost = P[t] + A[j][t-1] + A[t+1][i+j-1]
			If Cost < MinCost: MinCost = Cost; 
A[j][i+j-1] = MinCost; 
MinCost = +∞;

Conclusion
By this, we can successfully calculate the cost of the optimal BST, given the set of value V and its set of frequencies P. However, I have not introduced how we can construct an optimal BST. Indeed, we can reconstruct an optimal BST by iterating backwards through the array A in the pseudocodes. I will leave this part for you to think through. It is not difficult but an interesting one. With that being said, this essay will come to an end. I hope you enjoy this. Thanks.

Best,
Ben