统计学相关

Bernie_Ly

已于 2025-09-02 21:53:04 修改

阅读量817

点赞数 9

CC 4.0 BY-SA版权

文章标签：算法

于 2025-08-24 16:27:39 首次发布

本文链接：https://blog.csdn.net/Bernie_Ly/article/details/150702920

✅步骤 5：计算置信区间（非合并方差，更真实）

✅6：结论

✅ 7：一句话总结

零、AB测试中的Z检验流程（双尾检验）

✅场景

某购物网站要测试新结算页面是否提升转化率：

A组（旧页面）：曝光 n1=1000，转化 x1=100 → 转化率 p^1=100/1000=0.10
B组（新页面）：曝光 n2=1000，转化 x2=130 → 转化率 p^2=130/1000=0.13

问题：新页面是否显著提升转化率？提升范围是多少？

✅步骤 1：写出假设

原假设 H₀：p1 = p2（新旧页面无差异）
备择假设 H₁：p1 ≠ p2（新页面有差异）

✅步骤 2：计算合并比例

在 H₀ 下假设总体比例相同，用合并比例估计：

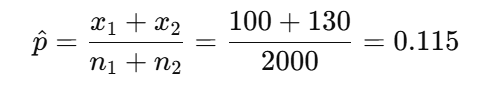
✅步骤 3：计算标准误（SE）

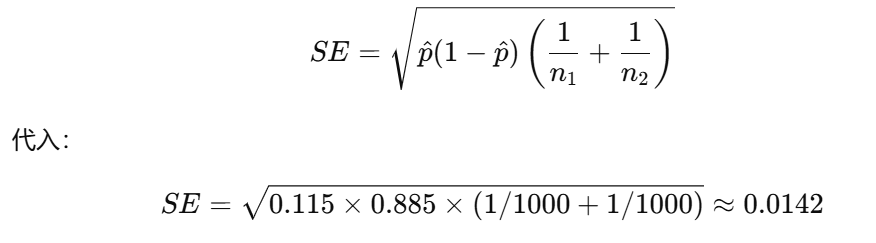
✅步骤 4：计算 Z 值（显著性公式）

✅步骤 5：计算置信区间（非合并方差，更真实）

✅6：结论

统计上显著（p=0.035 < 0.05）→ 拒绝 H0，A 与 B 的转化率确实不同。
提升幅度大约 3%，真实提升范围在 0.25% ~ 5.75% 之间。
置信区间完全大于 0 → 可以认为新页面确实优于旧页面。

✅ 7：一句话总结

“本次 AB 实验 B 组的转化率比 A 组高 3%，

Z 检验显著（p=0.035），

95% 置信区间 [0.25%, 5.75%]，

说明新页面大概率能带来正向提升，可以上线。”

一、T检验与Z检验

✅1.T检验与Z检验的含义

Z检验
- 基于正态分布（标准正态分布 Z ~ N(0,1))。
- 用来检验样本均值、样本比例与总体参数之间的差异是否显著。
- 前提是 总体方差已知 或 样本量足够大（通常 n ≥ 30，根据中心极限定理近似正态分布）。
T检验
- 基于 Student’s t 分布。
- 用来在 总体方差未知且样本量较小（n < 30） 的情况下，检验样本均值与总体均值、或两个样本均值之间的差异是否显著。
- t分布相较于正态分布更加“厚尾”，对小样本的随机波动更敏感。

✅2.主要区别

特点	Z检验	T检验
样本量	大样本（一般 ≥ 30）	小样本（一般 < 30）
总体方差	已知	未知
分布	标准正态分布	t分布，自由度 = n - 1
应用场景	总体参数已知或可近似已知	总体参数未知，依赖样本估计
稳健性	较依赖大样本和已知方差	对小样本友好

✅3.具体使用场景

Z检验适用场景
- 大样本均值检验（例如 n=100 的样本均值是否等于某个总体均值）。
- 总体方差已知的情况。
- 比例检验（例如市场调研中，5000人样本里 A 产品支持率与50%是否显著不同）。
T检验适用场景
- 样本量小，总体方差未知（比如从 15 个顾客中抽样测评满意度，判断是否显著高于某个标准值）。
- 两个小样本之间的均值比较（独立样本 t 检验、配对样本 t 检验）。
- 单样本 t 检验：样本均值 vs 理论均值。

✅ 4.一句话总结

已知总体方差 + 大样本 → Z检验

未知总体方差 + 小样本 → T检验

二、AB实验中的比率指标检验

✅1. 为什么比率指标用 Z 检验？

比率型指标（转化率 p = 成功次数 / 总样本数）本质上符合 二项分布。
当样本量足够大时，根据中心极限定理，二项分布可以近似为正态分布。
在这种情况下，我们可以用 Z检验 来对两个比例差异进行显著性检验。

比如：

A 组转化率 = 10% (n=5000)
B 组转化率 = 12% (n=5000)
就可以用 Z 检验来判断 12% 是否显著高于 10%。

✅2. 为什么不是 T 检验？

T 检验更多用于 均值检验，特别是样本量小、总体方差未知的情况。
而比率型指标的分布并不是连续的正态分布，而是离散的二项分布。只有在大样本下近似正态化，才能套用 Z 检验。
因此在 AB 实验里，通常不会用 T 检验来处理比率指标。

✅3. 实操注意事项

在 AB 实验中使用 Z 检验时，需要满足几个条件：

样本量足够大（经验上 n ≥ 30，实践中常常要求更大，比如 n ≥ 1000），确保二项分布近似正态分布。
正交分流：流量分配要独立随机，避免干扰。
护栏指标：比如保证分流后的样本量均衡，曝光量没有显著偏差。
双侧检验还是单侧检验：通常 AB 实验默认用双侧检验（更严谨），除非目标是验证是否“显著提升”。

✅ 4.一句话总结

在 AB 实验里，比率指标（转化率、留存率等）→ Z 检验；
而 均值类指标（平均停留时长、客单价等）→ T 检验（在总体方差未知时）。

✅ 5. 中心极限定理

(Central Limit Theorem, CLT)

定义：
当样本容量足够大时，不管原始总体分布是什么（哪怕是偏态分布、二项分布等），样本均值的分布都会趋近于一个正态分布.

经验规则：

当 n 足够大，并且 np ≥ 5 且 n(1-p) ≥ 5 时，二项分布就可以近似用正态分布。

在 AB 实验里，因为样本量往往是几千、几万，条件完全满足，所以用 Z 检验是合理的。

三、置信区间

(Confidence Interval, CI)

✅1. 含义

直观理解：置信区间是一段“范围”，告诉你 总体真实参数（比如真实转化率提升）大概率落在这个区间里。
它不是“95% 的概率参数在区间内”，而是：如果我们不断重复抽样做实验，95% 的实验会得到一个包含真实参数的区间。
举例：
- 我们估计 B 组转化率比 A 组高 2%。
- 95% CI = [0.8%, 3.2%]。
- 这表示我们有 95% 的信心认为，真实提升幅度介于 0.8% 和 3.2% 之间。

✅2. 在 AB 实验中的作用

补充显著性检验

p 值只能告诉我们“有没有差异”，但没告诉我们“差异有多大”。
置信区间能同时反映方向（正/负）和幅度（提升多少）。

判断结果的业务价值

比如：
- 提升显著，但 CI = [0.1%, 0.5%]，虽然显著，但提升幅度很小，可能业务意义不大。
- 提升 不显著，但 CI = [-0.2%, +1.8%]，说明可能有小幅提升，需要更大样本再验证。

评估结果的稳定性与不确定性

CI 越窄 → 实验结果越稳定、结论越可靠。
CI 越宽 → 样本量不足，结果不确定性大。

辅助决策

如果 CI 整个区间都 高于 0，说明实验组 必然比对照组好。
如果 CI 跨过 0（比如 [-1%, 2%]），说明可能好可能差，不确定。
如果 CI 整个区间都低于 0，说明实验组比对照组差。

✅3. 举个实际例子

假设 AB 实验结果：

A 组转化率 = 10%
B 组转化率 = 12%
提升 = 2%
95% CI = [0.8%, 3.2%]

解读：

提升显著（p < 0.05，CI 不包含 0）。
我们有 95% 的信心认为，B 组比 A 组 至少提升 0.8%，最多提升 3.2%。
如果业务期望的最低提升是 0.5%，那么这个实验结果有价值。

✅ 4.一句话总结

置信区间是在 AB 实验里比 “显著/不显著” 更有价值的指标，它告诉我们 真实效果可能的范围，帮助判断结果是否 既显著又有业务意义。

四、单尾检验及双尾检验

✅1. 含义

双尾检验 ( Two - tailed Test )
- 检验假设：差异是否存在（可能更大或更小）。
- 原假设 H0：μ = μ0
- 备择假设 H1：μ ≠ μ0
- 拒绝域在分布的两端（左右两边）。
- 常用阈值 α = 0.05 → 左右各分配 0.025。
单尾检验 (One-tailed Test)
- 检验假设：差异是否 在某一个方向上（只关注大于或小于）。
- 原假设 H0：μ = μ0
- 备择假设 H1： μ > μ0 或 H1：μ < μ0
- 拒绝域只在一端。
- α = 0.05 全部分配在一边。

✅2. 区别

特点	双尾检验	单尾检验
假设形式	H1：μ ≠ μ0	H1： μ > μ0 或 H1：μ < μ0
检验目标	检验差异是否存在（方向不限）	检验差异是否朝特定方向发展
拒绝域	分布两端，各占 α/2	分布一端，占 α
灵敏度	更保守，不容易拒绝 H0	更灵敏，容易在指定方向上显著
应用场景	探索性实验、学术研究	验证性实验、方向已知的业务假设

✅3. 举例

(1) 双尾检验

问题：某药物对血压的影响。
假设原均值 = 120 mmHg。
研究者想知道“药物是否会改变血压”，不管升高还是降低。
检验：H0: μ = 120，H1: μ ≠ 120。
→ 用 双尾检验。

(2) 单尾检验

问题：AB实验测试新页面是否提高转化率。
假设对照组转化率 = 10%。
团队只关心“新页面是否更好”，不关心“是否更差”。
检验：H0 : pnew=0.10，H1 : pnew>0.10。
→ 用 单尾检验。

✅4. 应用场景总结

在 AB 实验中，如果我们只关心某个功能是否提升转化率，可以使用 单尾检验，因为功效更高、样本量要求更低；
但如果实验目标是探索性的，或平台为了保证科学性和避免滥用，通常默认使用 双尾检验，然后结合方向来解读。
因此，实际业务里一般 默认双尾，更严谨；若事先设定只关心提升，则用单尾。

双尾检验
- 学术研究 → 需要中立性，既关心增加也关心减少。
- 探索性实验 → 不确定结果方向。
单尾检验
- 业务实验 → 已有明确方向（比如“新功能不会比旧的差，只关心能否更好”）。
- 医疗试验 → 新药只能更安全/更有效，否则直接淘汰。

✅5. 一句话总结

双尾检验 → 看有没有差异（保守，学术/探索用）。

单尾检验 → 看差异是否朝预期方向发展（效率高，业务/验证用）。

五、MDE

（Minimum Detectable Effect，最小可检测效应）

🔍 1. 什么是 MDE？

定义：MDE 是在给定的统计假设检验条件下（显著性水平 α、检验功效 1-β：在真实存在差异时，实验能正确拒绝原假设的概率。），实验能够检测到的最小差异（效应大小）。
通俗理解：
- 就像你拿着一个放大镜（AB实验），MDE 表示“这个放大镜最小能看见的差异”。
- 如果真实差异比 MDE 大 → 实验有较大概率发现。
- 如果真实差异比 MDE 小 → 实验可能看不出来（统计上不显著）。

🧮 2. 数学表达

假设我们比较两组比例（如转化率），则 MDE 通常表示为一个百分比提升：

MDE=最小可检测差异=Δp

与 样本量 n 的关系：

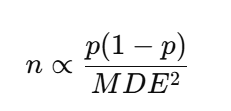
（忽略常数项 α 和 β 的影响）

含义：

1.样本量越大 → MDE 越小（能检测到更微小的差异）。

2.样本量越小 → MDE 越大（只能检测到很大的差异）。

⚖️ 3. 影响 MDE 的因素

1.样本量 (n)

n ↑ → MDE ↓

大样本能避免噪声干扰，检测到更小的效果

2.基准转化率 (p)

MDE 与 p(1−p)成正比。

p=0.5 时方差最大 → MDE 较大；p 越接近 0 或 1 → MDE 较小。

3.显著性水平 (α)

α 越严格（比如 0.01 而不是 0.05） → MDE ↑

4.检验功效 (1-β, Power)

功效越高（90% vs 80%） → MDE ↑

📊 4. 举例

例子回顾：

A组：转化率 10% (p1=0.10，n1=1000)
B组：转化率 13% (p2=0.13，n2=1000)
已知结果差异 = 3 个百分点

MDE 计算逻辑：

在实验设计阶段，我们会反过来：已知 样本量 n=1000/组，基准率 10%，问：
“在 α=0.05, Power=0.8 下，最小能检测的差异是多少？”

步骤：

1.确定 α=0.05 → 临界值 Zα/2 = 1.96

2.确定功效 0.8 → β=0.2 → Zβ = 0.84

3.基准方差 ≈ p(1-p) = 0.1×0.9 = 0.09

4.带入近似公式

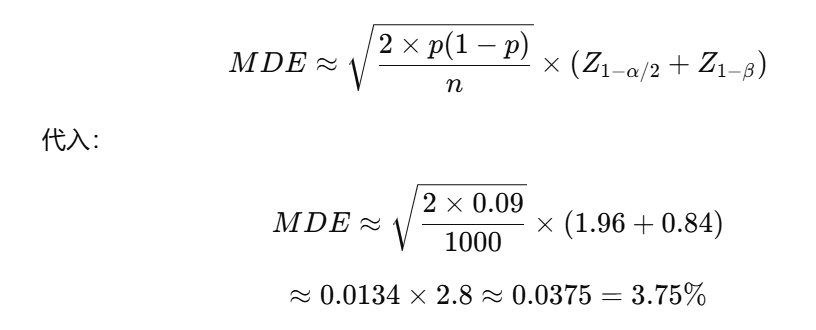
🚀 5. 在 AB 实验中的作用

实验设计前：
- 决定所需样本量。
- 如果业务只关心 ≥5% 的提升，就不用设计到能检测 1% 提升（节省样本）。
实验解读时：
- 如果实验没显著，可能是差异小于 MDE，不代表没有差异，而是“检测不出来”。
资源分配：
- MDE 设定得太小 → 样本需求过大，实验跑不动。
- MDE 设定得太大 → 小幅收益可能被忽略，错失优化机会。

⚠️ 6. 如何直观理解“ MDE 越小 → 样本需求指数级增加”

大差异好比“大象”：
- 如果实验组转化率从 10% 跳到 15%，提升非常明显。
- 即使样本量不多，也能一眼看出来“B 组比 A 组好”。
- 就像在操场上找一头大象，几个人也能发现。
小差异好比“蚂蚁”：
- 如果实验组从 10% 提升到 10.3%，提升非常细微。
- 很容易被日常波动“淹没”。
- 就像操场上找一只蚂蚁，你需要成千上万的人去一起观察，才能保证能找到。
指数级原因：
- 差异减半（比如 2% → 1%），随机噪声的比例影响更大。
- 要把这种噪声压下去，就必须多采集几倍数据（常常是 4 倍）。
- 所以你要检测的提升越“小”，需要的样本数就像雪球一样迅速变大。

六、显著性水平 α、Z 值、p 值

✅1. 概念区分

显著性水平 α
- 是 事先人为设定的阈值，常取 0.05。
- 含义：在“原假设 H₀ 成立”的情况下，我允许犯 I 类错误（错杀无罪）的最大概率。
- 人话：我愿意冒 5% 的风险，把其实没效果的功能错当有效上线。
- 比如 α=0.05，就是“有 ≤5% 的概率在 H₀ 为真时仍然拒绝它”。
Z 值
- 是根据样本统计量（比如两组 CTR 的差异 Δ）和其标准误 SE 计算出来的标准化统计量：
  Z=观察到的差异标准误Z = \frac{\text{观察到的差异}}{\text{标准误}}Z=标准误观察到的差异
- 它反映了“观察结果距离 H₀ 假设下期望值有多少个标准差”。
p 值
- 是在 H₀ 为真时，观察到 当前或更极端结果 的概率。
- 人话：如果世界上真的没有效果（H₀ 成立），我随机碰巧看到这么大（甚至更大）效果的概率是多少。
- 具体计算：先把 Z 值算出来，再用标准正态分布表查到对应的尾部概率。
  - 双尾检验：p 值 = 2 × P(Z ≥ |Z_obs|)
  - 单尾检验：p 值 = P(Z ≥ Z_obs)