LSTM前向传播与反向传播算法推导（非常详细）

1.长短期记忆网络LSTM

LSTM(Long short-term memory)通过刻意的设计来避免长期依赖问题，是一种特殊的RNN。长时间记住信息实际上是 LSTM 的默认行为，而不是需要努力学习的东西！

所有递归神经网络都具有神经网络的链式重复模块。在标准的RNN中，这个重复模块具有非常简单的结构，例如只有单个tanh层，如下图所示。
[外链图片转存失败(img-EwKxtSFp-1569051242265)(./images/lstm-rnn.jpg)]
LSTM具有同样的结构，但是重复的模块拥有不同的结构，如下图所示。与RNN的单一神经网络层不同，这里有四个网络层，并且以一种非常特殊的方式进行交互。

1.1 LSTM–遗忘门

LSTM 的第一步要决定从细胞状态中舍弃哪些信息。这一决定由所谓“遗忘门层”的 S 形网络层做出。它接收 $h_{t-1}$ 和 $x_t$，并且对细胞状态 $C_{t-1}$ 中的每一个数来说输出值都介于 0 和 1 之间。1 表示“完全接受这个”，0 表示“完全忽略这个”。

1.2 LSTM–输入门

下一步就是要确定需要在细胞状态中保存哪些新信息。这里分成两部分。第一部分，一个所谓“输入门层”的 S 形网络层确定哪些信息需要更新。第二部分，一个 tanh 形网络层创建一个新的备选值向量—— ${\tilde{C}}_t$，可以用来添加到细胞状态。在下一步中我们将上面的两部分结合起来，产生对状态的更新。

1.3 LSTM–细胞状态更新

现在更新旧的细胞状态 $C_{t-1}$ 更新到 $C_t$。先前的步骤已经决定要做什么，我们只需要照做就好。
我们对旧的状态乘以 $f_t$，用来忘记我们决定忘记的事。然后我们加上 $i_t\odot {\tilde{C}}_t$，这是新的候选值，根据我们对每个状态决定的更新值按比例进行缩放。

1.4 LSTM–输出门

最后，我们需要确定输出值。输出依赖于我们的细胞状态，但会是一个“过滤的”版本。首先我们运行 S 形网络层，用来确定细胞状态中的哪些部分可以输出。然后，我们把细胞状态输入 tanh（把数值调整到 −1 和 1 之间）再和 S 形网络层的输出值相乘，部这样我们就可以输出想要输出的分。

1.5 LSTM的变种

目前我所描述的还只是一个相当一般化的 LSTM 网络。但并非所有 LSTM 网络都和之前描述的一样。事实上，几乎所有文章都会改进 LSTM 网络得到一个特定版本。差别是次要的，但有必要认识一下这些变种。

（1） 一个流行的 LSTM 变种由 Gers 和 Schmidhuber 提出，在 LSTM 的基础上添加了一个“窥视孔连接”，这意味着我们可以让门网络层输入细胞状态。

上图中我们为所有门添加窥视孔，但许多论文只为部分门添加.

（2）另一个变种把遗忘和输入门结合起来。同时确定要遗忘的信息和要添加的新信息，而不再是分开确定。当输入的时候才会遗忘，当遗忘旧信息的时候才会输入新数据。

（3）一个更有意思的 LSTM 变种称为 Gated Recurrent Unit（GRU），由 Cho 等人提出。GRU 把遗忘门和输入门合并成为一个“更新门”，把细胞状态和隐含状态合并，还有其他变化。这样做使得 GRU 比标准的 LSTM 模型更简单，因此正在变得流行起来。

2.LSTM前向传播与反向传播

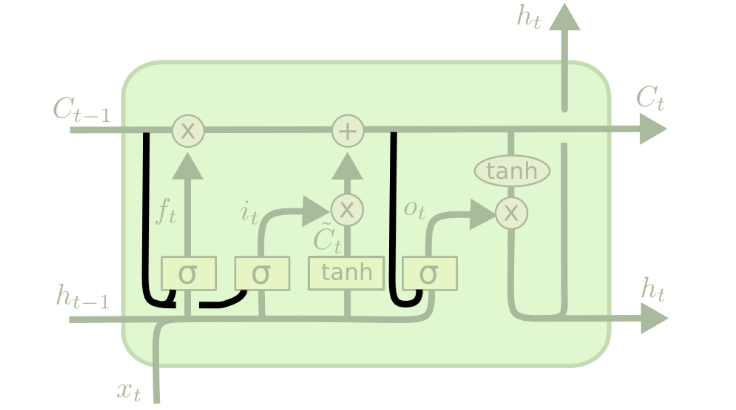
本小节只推导添加“窥视孔连接”的变种LSTM，如下图所示，其它LSTM变种的推导方法与该方法类似，这里不做过多介绍。对反向传播算法了解不够透彻的，请参考https://zhuanlan.zhihu.com/p/79657669 ，这里有详细的推导过程，本文将直接使用https://zhuanlan.zhihu.com/p/79657669的结论。

为了更直观的推导反向传播算法，将其转化为右图所示形式。

2.1 LSTM前向传播

LSTM在t时刻的前向传播公式为：
$$\{\begin{array}{l}{i}_t=\sigma ({\tilde{i}}_t)=\sigma (W_{xi}{x}_t+W_{hi}{h}_{t-1}+W_{ci}{c}_{t-1}+b_i)\\ f_t=\sigma ({\tilde{f}}_t)=\sigma (W_{xf}{x}_t+W_{hf}{h}_{t-1}+W_{cf}{c}_{t-1}+b_f)\\ g_t=\tanh ({\tilde{g}}_t)=\tanh (W_{xg}{x}_t+W_{hg}{h}_{t-1}+b_g)\\ o_t=\sigma ({\tilde{o}}_t)=\sigma (W_{xo}{x}_t+W_{ho}{h}_{t-1}+W_{co}{c}_t+b_o)\\ c_t=c_{t-1}\odot f_t+g_t\odot i_t\\ m_t=\tanh (c_t)\\ h_t=o_t\odot m_t\\ y_t=W_{yh}{h}_t+b_y\end{array}$$

2.2 LSTM反向传播

已知：$\frac{\partial J}{\partial y_t},\frac{\partial J}{\partial c_{t+1}},\frac{\partial J}{\partial {\tilde{o}}_{t+1}},,\frac{\partial J}{\partial {\tilde{f}}_{t+1}},\frac{\partial J}{\partial {\tilde{i}}_{t+1}},\frac{\partial J}{\partial {\tilde{g}}_{t+1}}$,求某个节点梯度时，首先应该找到该节点的输出节点，然后分别计算所有输出节点的梯度乘以输出节点对该节点的梯度，最后相加即可得到该节点的梯度。如计算$\frac{\partial J}{\partial h_t}$时，找到$h_t$节点的所有输出节点$y_t、{\tilde{o}}_{t+1}、{\tilde{f}}_{t+1}、{\tilde{i}}_{t+1}、{\tilde{g}}_{t+1}$，然后分别计算输出节点的梯度(如$\frac{\partial J}{\partial y_t}$)与输出节点对$h_t$的梯度的乘积（如$\frac{\partial J}{\partial y_t}{W}_{yh}^T$），最后相加即可得到节点$h_t$的梯度:
$$\frac{\partial J}{\partial h_t}=\frac{\partial J}{\partial y_t}{W}_{yh}^T+\frac{\partial J}{\partial {\tilde{o}}_{t+1}}{W}_{ho}^T+\frac{\partial J}{\partial {\tilde{f}}_{t+1}}{W}_{hf}^T+\frac{\partial J}{\partial {\tilde{i}}_{t+1}}{W}_{hi}^T+\frac{\partial J}{\partial {\tilde{g}}_{t+1}}{W}_{hg}^T$$
同理可得t时刻其它节点的梯度：
$$\{\begin{array}{l}\frac{\partial J}{\partial h_t}=\frac{\partial J}{\partial y_t}{W}_{yh}^T+\frac{\partial J}{\partial {\tilde{o}}_{t+1}}{W}_{ho}^T+\frac{\partial J}{\partial {\tilde{f}}_{t+1}}{W}_{hf}^T+\frac{\partial J}{\partial {\tilde{i}}_{t+1}}{W}_{hi}^T+\frac{\partial J}{\partial {\tilde{g}}_{t+1}}{W}_{hg}^T\\ \\ \frac{\partial J}{\partial m_t}=\frac{\partial J}{\partial h_t}\odot o_t\\ \\ \frac{\partial J}{\partial c_t}=\frac{\partial J}{\partial m_t}\frac{d{m}_t}{d{c}_t}+\frac{\partial J}{\partial c_{t+1}}\odot f_{t+1}+\frac{\partial J}{\partial {\tilde{f}}_{t+1}}{W}_{cf}^T+\frac{\partial J}{\partial {\tilde{i}}_{t+1}}{W}_{ci}^T\\ \\ \begin{array}{l}\frac{\partial J}{\partial g_t}=\frac{\partial J}{\partial c_t}\odot i_t\\ \frac{\partial J}{\partial i_t}=\frac{\partial J}{\partial c_t}\odot g_t\\ \frac{\partial J}{\partial f_t}=\frac{\partial J}{\partial c_t}\odot c_{t-1}\\ \frac{\partial J}{\partial o_t}=\frac{\partial J}{\partial h_t}\odot m_t\end{array}\}\Rightarrow \{\begin{array}{l}\frac{\partial J}{\partial {\tilde{g}}_t}=\frac{\partial J}{\partial g_t}(1-g_t^2)\\ \frac{\partial J}{\partial {\tilde{i}}_t}=\frac{\partial J}{\partial i_t}{i}_t(1-i_t)\\ \frac{\partial J}{\partial {\tilde{f}}_t}=\frac{\partial J}{\partial f_t}{f}_t(1-f_t)\\ \frac{\partial J}{\partial {\tilde{o}}_t}=\frac{\partial J}{\partial o_t}{i}_t(1-o_t)\end{array}\\ \\ \frac{\partial J}{\partial x_t}=\frac{\partial J}{\partial {\tilde{o}}_t}{W}_{xo}^T+\frac{\partial J}{\partial {\tilde{f}}_t}{W}_{xf}^T+\frac{\partial J}{\partial {\tilde{i}}_t}{W}_{xi}^T+\frac{\partial J}{\partial {\tilde{g}}_t}{W}_{xg}^T\end{array}$$

对参数的梯度：
$$\{\begin{array}{l}\frac{\partial J}{\partial W_{ho}}=h_t^T\frac{\partial J}{\partial {\tilde{o}}_{t+1}}\\ \frac{\partial J}{\partial W_{hf}}=h_t^T\frac{\partial J}{\partial {\tilde{f}}_{t+1}}\\ \frac{\partial J}{\partial W_{hi}}=h_t^T\frac{\partial J}{\partial {\tilde{i}}_{t+1}}\\ \frac{\partial J}{\partial W_{hg}}=h_t^T\frac{\partial J}{\partial {\tilde{g}}_{t+1}}\end{array}\{\begin{array}{l}\frac{\partial J}{\partial W_{yh}}=h_t^T\frac{\partial J}{\partial y_t}\\ \frac{\partial J}{\partial W_{cf}}=c_t^T\frac{\partial J}{\partial {\tilde{f}}_{t+1}}\\ \frac{\partial J}{\partial W_{ci}}=c_t^T\frac{\partial J}{\partial {\tilde{i}}_{t+1}}\\ \frac{\partial J}{\partial W_{co}}=c_t^T\frac{\partial J}{\partial {\tilde{o}}_t}\end{array}\{\begin{array}{l}\frac{\partial J}{\partial W_{xo}}=x_t^T\frac{\partial J}{\partial {\tilde{o}}_t}\\ \frac{\partial J}{\partial W_{xf}}=x_t^T\frac{\partial J}{\partial {\tilde{f}}_t}\\ \frac{\partial J}{\partial W_{xi}}=x_t^T\frac{\partial J}{\partial {\tilde{i}}_t}\\ \frac{\partial J}{\partial W_{xg}}=x_t^T\frac{\partial J}{\partial {\tilde{g}}_t}\end{array}$$

参考资料：https://www.cnblogs.com/xuruilong100/p/8506949.html