宋浩老师《线性代数》笔记（第一章行列式）
目录
1.1 行列式
1.1.1二阶，三阶行列式和排序
1. 二阶行列式：2行2列4个元素
主对角线 （a11和a22）。次对角线（a12和a21）。
2.三阶行列式：3行3列9个元素
3. 排列
定义：由1，2，3，···，n 组成的一个有序数值叫n级排列。
例1：123 132 213 这是3级排列
例2：3145 不是4级排列，也不是5级排列
排列中的几个常见概念
1，n级排列的个数：n*（n-1）···3*2*1
2，逆序定义：大的数排在小的数前面 例如：43
3，逆序数定义：逆序的总数 N（4213）= 3+1
4，偶排列和奇排列：
5，N级标准排列（自然排列）N（1*2*3···(n-1)*n）= 0
6，N(n(n-1)``3*2*1)= n-1+n-2+```3+2+1=n(n-1)/2
7，对换：
一个排列进行一个对换，奇偶性改变
8，在n级排列中，奇排列和偶排列各占一半
注意：数逆序数时，从第一个开始数，顺序不能乱。
1.1.2 n阶行列式
将行列式按行展开步骤
1，行标取标准排列之后。
2，列标取排列的所有可能。
3，从不同行不同列取出n个元素相乘。
4，符号由列标排列的奇偶性决定。
注意：还可以按列展开，也可以既不按行也不按列展开
特殊的行列式计算
推广到下三角，上三角行列式等于主对角线的乘积
1.2 行列式的性质
1，转置
对行成立的性质，对列也成立
2，两行互换，值变号
推论：行列式两行（列）对应相等，行列式等于0
3，某一行都乘以k，等于用k乘以k
4，两行（列）对应成比例 D=0
5.，行列式相加
注意：是和的那一行分开，其余行保持不变
6， 某一行（列）乘以一个数，加到另一行（列）上去，行列式结果不变
这个性质对行列式的计算贡献很大，用于将行列式转化成上三角形式
1.3 行列式按行展开
1，行列式按行（列）展开（余子式和代数余子式）
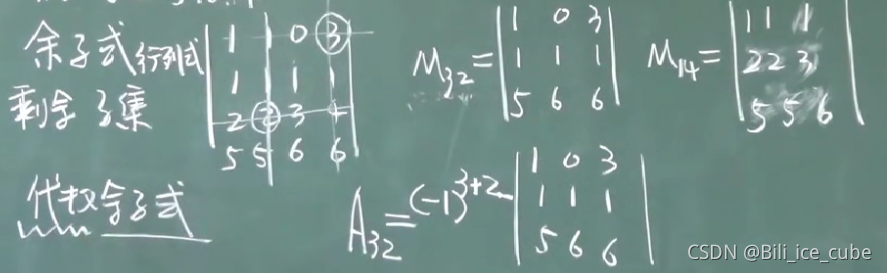
某一行的每一个元素与对应的代数余子式相乘之和
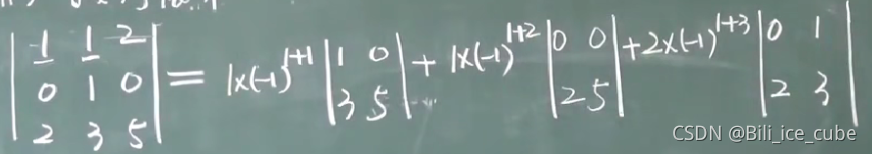
注意：该方法有降阶的功能。展开时，选用0多的行（列）展开
2，异乘变零定理
某行元素与另一行元素的代数余子式乘积之和等于0
3，拉普拉斯定理
取定k行，由k行元素组成的所有K阶子式与代数余子式乘积之和等于0，同样也是选择0多的行
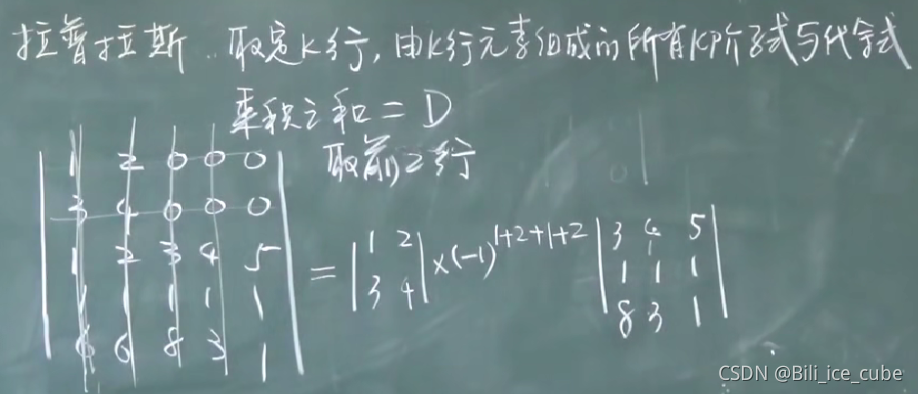
4，行列式相乘定理
同阶行列式相乘：第一个行列式的行的每个元素分别与第二个行列式的列的元素对应相乘之和
不同阶相乘：1，将两个行列式分别计算出来，再相乘。2，使用按行展开方法降阶（不常用）
1.4 行列式的计算
1，使用行列式性质将行列式变成上三角形式
注意：1，注意观察行列式，灵活使用两行变换方法（注意变号），将第一行变成1
2，处理的时候按顺序计算。
2，使用按行展开方法计算
3，特殊行列式计算
a，制造行和
b，加边法（不能改变行列式的值）
注意：三叉形行列式的解题方法：使用对角线消除第一列
c，范德蒙行列式
d，反对称行列式
注意：反对称行列式为奇数阶，则行列式等于0（将所有行都乘以一个负号就相当于对行列式做了一个转置，由于是奇数阶，左右-D=D=0）
1.5 克莱姆法则-解方程组
注意：1，只适用于方程个数=未知数个数
2，D！= 0 xj = Dj / D
3，计算量很大，不适合人工算，适合计算机计算
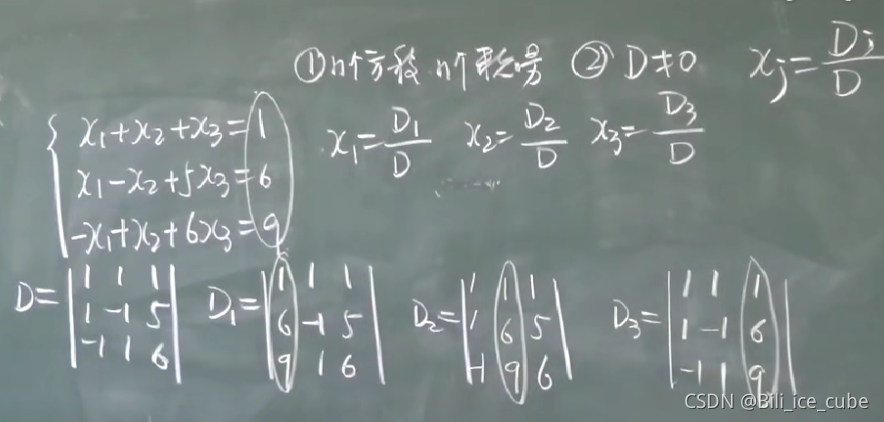
特殊：1，齐次方程组，至少有零解
2，如果D不等于0，只有零解
这里视频链接，大家可以配合食用。
扫一扫
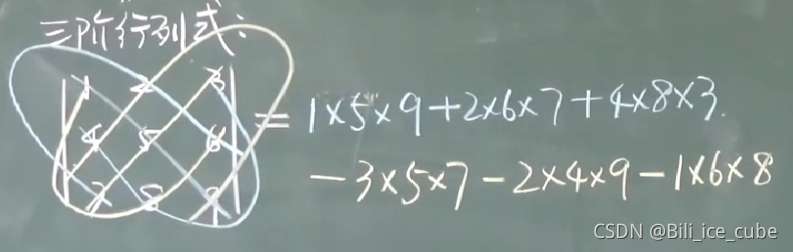
4万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
