宋浩老师《线性代数》笔记（第二章矩阵）（一）
目录
2.1 矩阵概念
1，实数矩阵和复数矩阵
2，行矩阵和列矩阵
3，注意数字0 和0矩阵的区别
4，负矩阵（矩阵前面添加负号）
5，行数等于列数的矩阵被称为方阵（方阵才有主对角线和次对角线）
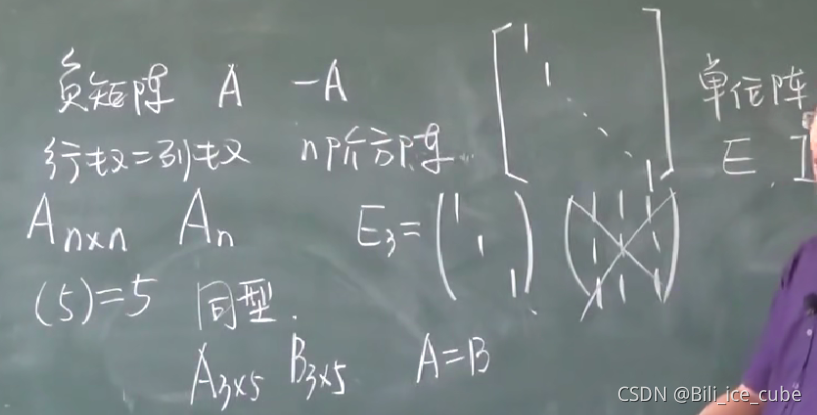
注意：矩阵相同的前提是同型矩阵 （两个o矩阵不一定相同）
2.2 矩阵运算
1，加法和减法（对应相加减，同型矩阵才能相加）
2，数乘（一个数乘以矩阵 == 数和矩阵中每一个元素乘积）和行列式不同
3，乘法（宋氏七字）
乘法性质中不满足的定理
a，AB ！= BA，AB有意义，BA不一定有意义。如果AB=BA，则A，B是可交换的（A，B都是同阶的方阵）
b，AB = 0 不能推出A=0或者B=0
c，AB = AC，当A ！= 0时，不能推出B=C
满足的定理
a，任意矩阵和零矩阵相乘，都等于零矩阵
b，任何矩阵和单位矩阵相乘，都等于本身
运算规律
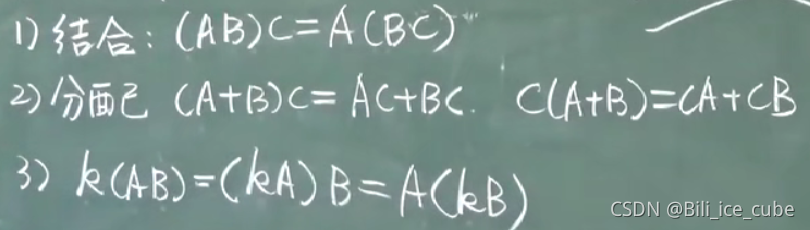
4，矩阵的幂运算（A的零次幂等于E）
注意：
常见例题讲解
5，矩阵的转置
2.3 特殊矩阵（方阵）
1，数量矩阵和对角性矩阵（区别是对角线上的值可以不同）
2，上三角形和下三角形矩阵
3，对称矩阵和反对称矩阵
对称矩阵的对角线的元素不一定
反对称矩阵主对角线为0
这里视频链接，大家可以配合食用。
扫一扫
4万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
