《球面天文学和天体力学引论》83.5节

瞎某某Blinder

已于 2024-04-23 11:58:46 修改

阅读量592

点赞数 5

分类专栏：天文文章标签：算法几何学抽象代数图论经验分享

于 2024-04-23 11:13:15 首次发布

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.csdn.net/Blindbaby123/article/details/138088847

版权

天文专栏收录该内容

4 篇文章

订阅专栏

本文用于记录本人在《球面天文学和天体力学》的天体力学引论的学习，所以思路会同原书大致相同，但是会加上本人的其他推导与思考，希望能向读者传输一些思想与经验，共同学习共同进步

大致是一周一更，每次更新大致为一节内容

所以，让我们开始吧

开普勒方程展开为时间的函数的公式

我们前文得到了单体与两体运动的轨道方程和运动学方程，为了决定行星在t时的位置，我们需要进行进一步的推理.

在下图中，S为太阳（椭圆焦点），B为行星（或彗星），P为近日点，A为远日点，ABP为该行星的运行轨道，而AB’P为以长轴为直径而绘制的辅助圆。

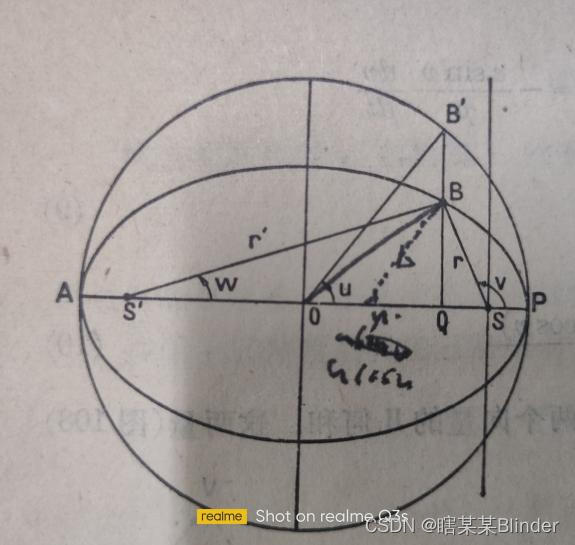
过B点，做B’Q垂直于AP，其中与辅助圆交于B’。由此就能得到三个角，偏近点角，平近点角，真近点角。

其中偏近点角为∠B’OP，平近点角为∠B’SP，真近点角为∠BSP

根据偏近点角的性质可知

$x_B=acosu$

$y_B=bsinu$

通过观察我们能知道，若想描述行星的位置坐标，偏近点角是格外重要的元素，这给我们一个思路，即求出u随时间t变化的函数，我们便能知道行星位置随时间变化的函数。

从此性质出发，在图中可得以下关系（3-1）

$rcos{v}=acos{u}-c$

$rsin{v}=bsin{u}$

进行整理后可得（3-2）

式3-1和式3-2的一式可以写为如下形式

两式相互加减可得（3-3）

于是可得（3-4）

$tan\frac{v}{2}=\sqrt{\frac{1+e}{1-e}}tan\frac{u}{2}$

我们求式3-4的微分可得

$\frac{dv}{{cos}^2\frac{v}{2}}=\sqrt{\frac{1+e}{1-e}}\frac{du}{{cos}^2\frac{u}{2}}$

整理可得

$\frac{dv}{du}=\sqrt{\frac{1+e}{1-e}}=\frac{{cos}^2\frac{v}{2}}{{cos}^2\frac{u}{2}}$

由式3-3中式一可得 $\frac{{cos}^2\frac{u}{2}}{{cos}^2\frac{v}{2}}=\frac{r}{a(1-e)}=\frac{{sin}^2\frac{u}{2}}{{sin}^2\frac{v}{2}}$ ，将该关系代入上式可得（3-5）

$dv/du=(a\sqrt(1-e²))/r=sinv/sinu$

根据万有引力有心力基本方程可得（3-6）

$r² dv/dt=D$

值得注意的是，式中的并非速度，而是真近点角，即理论力学讨论时常使用的。

将式3-6代入式3-5便能将替换，可得

$\frac{du}{dt}=\frac{2\pi a}{Tr}=\frac{2\pi}{T(1-ecosu)}$

积分后得到

$u-esinu=(2\pi(t-t_0))/T$

这便是我们所需的u随时间t变化的函数，叫做开普勒方程，值得注意的是，其中的为过近日点的时刻，前文提到的平近点角的表达式即为 $M=\frac{2\pi(t-t_0)}{T}$ 。这是与行星同时从近日点出发，以匀角速n运动的一点，在t时的真近点角。

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

打赏作者

瞎某某Blinder 你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20

扫码支付：¥1

获取中

扫码支付

您的余额不足，请更换扫码支付或充值

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。