[BZOJ2154]Crash的数字表格（莫比乌斯反演）

最新推荐文章于 2019-06-25 18:44:00 发布

wwyx2001

最新推荐文章于 2019-06-25 18:44:00 发布

阅读量321

点赞数 2

分类专栏：莫比乌斯反演

本文链接：https://blog.csdn.net/Blue_CuSO4/article/details/78723676

版权

莫比乌斯反演专栏收录该内容

14 篇文章 0 订阅

订阅专栏

题目：

我是超链接

题解：

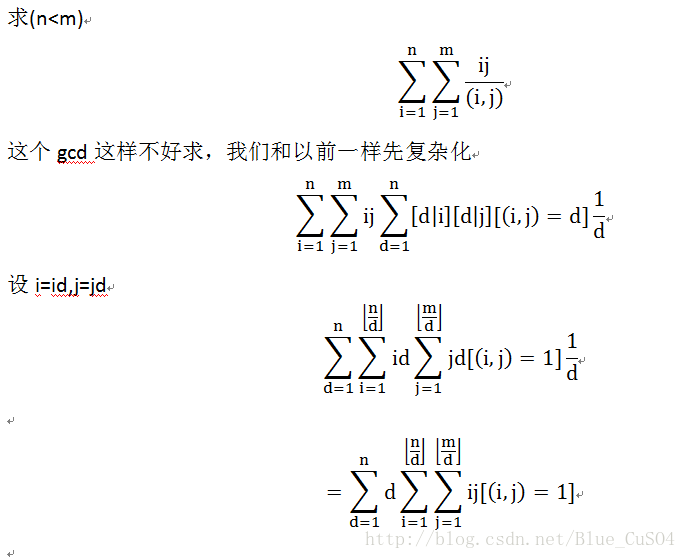
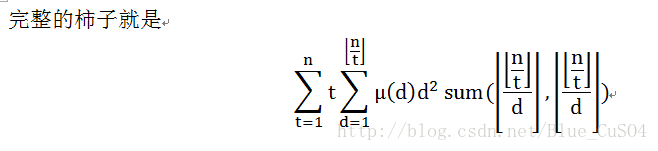
这里写图片描述

柿子就画到这里，一层层往回代就好了，这里的sum可以O(1)求出，F

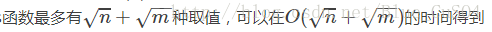
加上分块优化，这个复杂度基本是O(n)的

注意：最后的ans不要忘了+mod%）mod，sum的过程用一个语句很容易爆int

代码：

#include <cstdio>
#include <cstring>
#include <iostream>
#define LL long long
using namespace std;
const int mod=20101009;
const int N=1e7;
int pri[N+5],num,n,m;LL mu[N+5];
bool ss[N+5];
void get_mu()
{
    mu[1]=1;
    for (LL i=2;i<=n;i++)
    {
        if (!ss[i])
        {
            pri[++num]=i;
            mu[i]=-1;
        }
        for (int j=1;j<=num && pri[j]*i<=n;j++)
        {
            ss[pri[j]*i]=1;
            if (i%pri[j]==0)
            {
                mu[pri[j]*i]=0;
                break;
            }
            mu[pri[j]*i]=-mu[i];
        }
    }
    for (int i=1;i<=n;i++) mu[i]=(mu[i-1]+(LL)i*i%mod*mu[i]%mod)%mod;
}
LL sum(LL x,LL y)
{
    LL w1=((x+1)*x/2)%mod;
    LL w2=((y+1)*y/2)%mod;
    return w1*w2%mod;
}
LL F(LL n,LL m)
{
    if (n>m) swap(n,m);
    LL t=0,j;
    for (int d=1;d<=n;d=j+1)
    {
        j=min(n/(n/d),m/(m/d));
        t=((LL)(mu[j]-mu[d-1])%mod*(LL)sum(n/d,m/d)%mod+t)%mod;
    }
    return t;
}
int main()
{
    scanf("%d%d",&n,&m);
    if (n>m) swap(n,m);
    get_mu();LL ans=0;int j;
    for (int d=1;d<=n;d=j+1)
    {
        j=min(n/(n/d),m/(m/d));
        ans=(ans+(LL)(d+j)*(LL)(j-d+1)/2%mod*(LL)F(n/d,m/d)%mod)%mod;
    } 
    printf("%lld",(ans+mod)%mod);
}