高中数学：零点综合题型（拔高）

一、零点与交点

关键原则
1、数形结合
2、方程思想

例题1

解题思路
1、函数转化成方程
2、零点问题转化成交点问题
3、数形结合
4、对数运算法则（函数值的和 转化成 x的积）

二、分段函数零点

关键原则
1、分段函数分段看
2、数形结合
3、零点转交点，交点转零点

例题1

解题思路
1、画分段函数图像
2、零点转交点

三、复合函数零点（重难点）

关键原则
1、复合函数，通过换元，转化成方程组问题，然后，分内函数解与外函数解。
2、分别画内函数与外函数的图像
3、零点问题转化成交点问题
4、根据题设，观察函数图像，先内后外

例题1

解题步骤：
1、换元，将复合函数转化成方程组

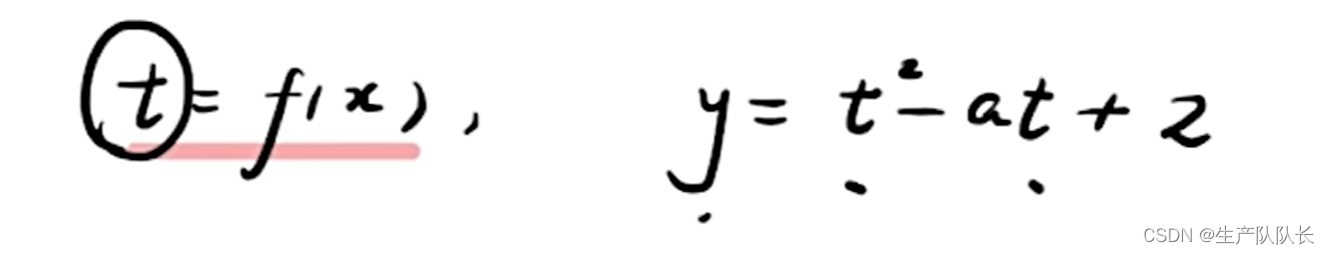
2、画图
内函数图像是左侧图像，外函数图像是右侧图像
我们可以发现，若想有6个交点，则t1和t2必须在1到2之间
然后，将问题转化成二次函数根的范围问题

3、求二次函数根的范围
这里采用分离参数法
同时，将零点问题，转化成交点问题
来找出a的范围

四、总结

零点转化成交点的题目，有以下几类
1、加减形式构建的组合函数

2、乘除形式构建的复合函数

组合函数，直接画图找焦点
复合函数，换元转化成内函数与外函数的方程组
外函数的解，作为水平直线与内函数找交点