一、函数零点
注意:函数零点是一个实数。不能写成坐标。

二、零点存在定理
注意:f(x)有零点 推不出 f(a)*f(b)<0


三、函数零点与图像交点的转化
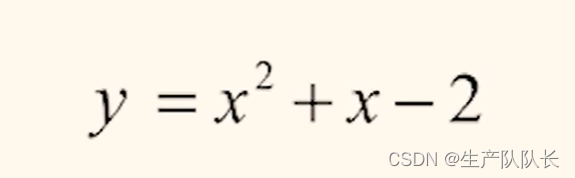
这个函数的函数图像的两种表示方法:
第一种:整体对待,看函数图像与x轴的交点


第二种:分成2个函数,观察这两个函数的交点。


四、例题
例题1
可以发现,下面三个函数都包含+x,于是,把三个函数分成两部分,用第二种画法找出零点即可。

例题2
如果偶函数只有一个零点,那么,这个零点必是:0,且 f(0)=0

例题3
解题关键:
1、画分段函数图像
2、f(f(x))-3=0 => f(m)=3,找出所有的m,再考虑 f(x)=m1、 f(x)=m2、 f(x)=m3...
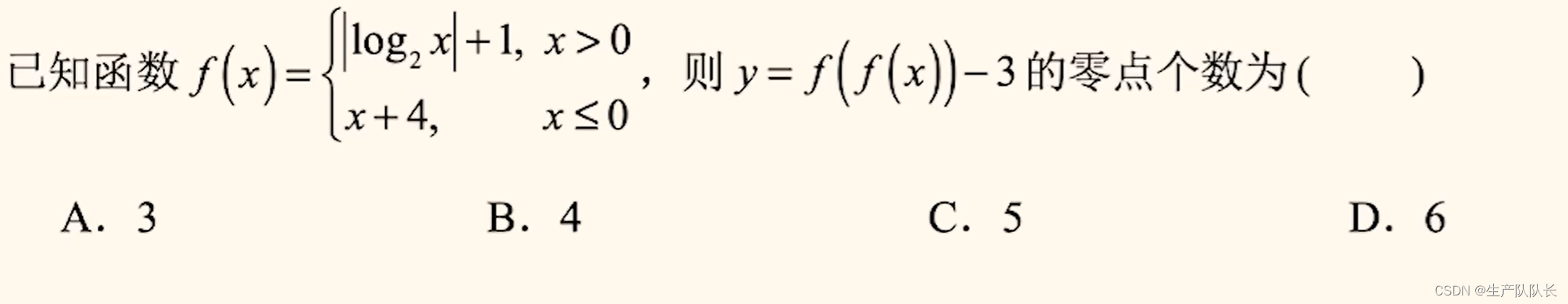








 本文探讨了函数零点的概念,包括零点存在定理的实际应用、函数图像与零点的关系,以及如何通过分段函数和偶函数性质解决例题。例题展示了如何通过分析函数结构找到零点的方法。
本文探讨了函数零点的概念,包括零点存在定理的实际应用、函数图像与零点的关系,以及如何通过分段函数和偶函数性质解决例题。例题展示了如何通过分析函数结构找到零点的方法。
















 628
628

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








