FFT简介
一种在O(nlogn)时间复杂度下把多项式(给定系数表达式)在系数表达式和点值表达式中互换的算法。
FFT的相关知识
一、多项式
1、定义:由若干个单项式相加组成的代数式叫做多项式(如: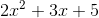
2、多项式的次数:组成多项式的单项式中,次数最高的单项式的次数,为该多项式的次数
3、多项式的次数界:多项式的次数加1
4、多项式的表示方法:
(1)、系数表示法:
如: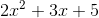
(2)、点值表示法:
把一个次数界为 n 多项式看成一个函数(如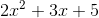
我们可以在这个函数上选 n 个的点来表示这个多项式。
如:(-1,4) (0,5) (1,10)
或:(-1,4) (2,19) (3,32)
这两组点值均可以表示多项式
why?
假设我们现在不知道原来的多项式
只知道(-1,4) (0,5) (1,10)这三个点值和该多项式的次数界为3
我们来求出原来的多项式:
首先,因为次数界为3,我们可以设该多项式为
然后,通过这三个点值,我们可以列出三个方程:
(不会打大括号)
三个方程足矣解三个未知数
解出方程后,我们就确定了这个多项式。
继续正题
5、多项式的运算
(1)、加减法:
使用系数表达式:O(n)
使用点值表达式(两个多项式的点值表达式中,点的横坐标均相等):O(n)
两个多项式:f(x) g(x)
f(x)的其中一个点值为(x,f(x))
g(x)的其中一个点值为(x,g(x))
则f(x)+g(x)的其中一个点值为(x,f(x)+g(x))
(2)、乘法:
使用系数表达式:O(n^2)
使用点值表达式(两个多项式的点值表达式中,点的横坐标均相等):O(n)
两个多项式:f(x) g(x)
f(x)的其中一个点值为(x,f(x))
g(x)的其中一个点值为(x,g(x))
则f(x)*g(x)的其中一个点值为(x,f(x)*g(x))
从多项式运算的时间复杂度来看,点值表达式是有很大优势的
所以我们想要把多项式由系数表达式转化为点值表达式
进行运算后,再将结果由点值表达式转化为系数表达式
但是,特别强调,
只有当两个多项式都选择了相同的2*N-1个x值来做点值表达式的横坐标时
两个多项式的点值表达式相加或相乘的时间复杂度才是O(N)
6、系数表达式与点值表达式的互换
(1)、系数表达式----->点值表达式(该过程称为求值)
(2)、点值表达式----->系数表达式(该过程称为插值)
7、多项式求值
求一个次数界为N的多项式需要N个点值
每求一个点的值都需要O(N)
所以,总时间复杂度为O(N^2)
8、多项式插值
(1)、高斯消元法O(N^3)
把N个点值看为N个方程,然后解出这个N元一次方程,得到系数表达式。
通过矩阵行行列列的加加减减运算来解出方程。。。(省略具体操作)
(2)、拉格朗日插值法O(N^2)
给定N个点值
我们可以构造一个N-1次的函数f(x),满足
我们可以对f(x)进行构造:
其中,
当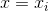
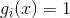
当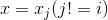
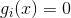
当![x!=x_{t}(t\in [1,N])](https://img-blog.csdnimg.cn/20181217224050983)
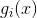
我们可以令
经过验证,我们可以发现
所以我们可以得出拉格朗日插值的公式:
通过一些预处理,可以使插值算法为O(N^2)。。。(省略具体操作)
二、复数
1、实数:有理数与无理数的总称
2、虚数单位i:
3、复数:形如z=a+bi(a,b均为实数)的数称为复数,其中a称为实部,b称为虚部,i称为虚数单位。
4、复数平面:
横轴x(也叫实轴)表示一个复数的实部
纵轴y(也叫虚轴)表示一个复数的虚部
一个复数可以看做在复数平面的一个向量:

如图,向量(2,3)就表示复数2+3i
5、复数的运算
A=a+bi,B=c+di
(1)、加法:
A+B=(a+bi)+(c+di)=(a+c)+(b+d)i
(2)、减法:
A-B=(a+bi)-(c+di)=(a-c)+(b-d)i
(3)、乘法:
A*B=(a+bi)*(c+di)=a*c+a*di+bi*c+bi*di=a*c+(a*d+b*c)i-b*d=(a*c-b*d)+(a*d-b*c)i
6、单位复数根:
形如:
如方程

其中0,1,2,3,4,5,6,7这些根分别记为
可以验算一下
可以得出:
这些根满足
(1)、消去引理: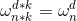
(2)、折半引理:如果为偶数,那么n个n次单位复根的平方的集合就是n/2个n/2次单位复数根的集合.
如:
(3)、求和引理:当k不是n的倍数时
可以自行画图验证
三、DFT(离散傅里叶变化)
对于次数界为n的多项式,
我们可以在处求值(也就是令x=
)
就可以得到一组f值:
我们称这一组f值为这组a值:()的DFT
FFT
FFT是一种算法。
它可以在O(nlogn)的时间复杂度计算出一组a值(系数向量)的DFT
它主要基于分治的策略。
设
所以就有
所以
求f(x)在的值
就可以转化为求
和
在
的值
然后,就可以递归下去,最后求出f(x)
由于单位复数根具有消去引理、折半引理、求和引理,所以它可以被选为求点值的点。
实际上我们还可以选择原根的次幂作为求值点(这就是NTT),这里就不展开了。
现在我们已经解决了系数表达式----->点值表达式。
那怎么解决点值表达式----->系数表达式呢?
我们可以把该过程看作两个矩阵相乘
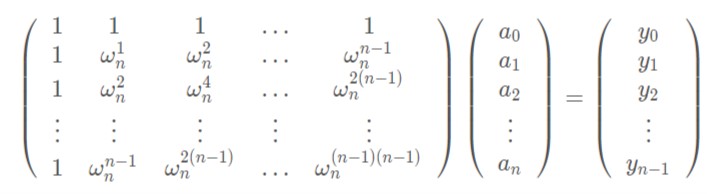
通过观察我们可以发现左边就是范德蒙德矩阵
它的逆矩阵很好求
于是点值表达式----->系数表达式的过程也可以用矩阵相乘的形式表达出来了。
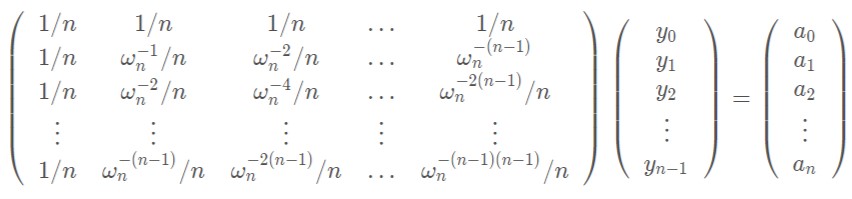
我们只需要在求值运算的基础上,稍作一些变换。
就可以在O(nlogn)的时间复杂度进行插值运算了。
但是注意,FFT的求值运算与插值运算只能求单位复数根在f(x)上的值,并不能进行任意点的多点求值与多点插值!!!
然而,递归实现并不是很好。
于是出现了非递归版的FFT。
我们可以观察一下FFT求值时系数向量a的变化
a每次递归被按照奇偶性分为两组
于是就有:

我们把最后一行a的编号写为二进制
a0 a4 a2 a6 a1 a5 a3 a7
000 100 010 110 001 101 011 111
然后在再把二进制反着写
000 001 010 011 100 101 110 111
再转换回来
0 1 2 3 4 5 6 7
于是我们发现,把每一个位置的二进制反着写就可以得到它对应的a的位置。
得到了最后的系数向量,我们就可以向上递推进行运算。
代码:
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 400005
#define LL long long
const double PI=3.1415926535897932384626;
struct cp{//定义复数结构与复数的运算
double r,i;
cp(){}
cp(double x,double y){r=x;i=y;}
cp operator + (const cp &t)const{return cp(r+t.r,i+t.i);}
cp operator - (const cp &t)const{return cp(r-t.r,i-t.i);}
cp operator * (const cp &t)const{return cp(r*t.r-i*t.i,r*t.i+i*t.r);}
}x[N],y[N],w,wn;
void change(cp a[],int len)//计算系数a的最后位置
{
int i,j,k;
for(i=1,j=len/2;i<len-1;i++){//在高位加1,向低位进位
if(i<j) swap(a[i],a[j]);
for(k=len/2;j>=k;j-=k,k>>=1);
j+=k;
}
}
void fft(cp a[],int len,int flg)
{
change(a,len);
int i,j,k;
for(i=2;i<=len;i<<=1){
wn=cp(cos(flg*2.0*PI/i),sin(flg*2.0*PI/i));
for(j=0;j<len;j+=i){
w=cp(1,0);
for(k=j;k<j+i/2;k++){
cp t=a[k];
cp u=a[k+i/2]*w;
a[k]=t+u;
a[k+i/2]=t-u;
w=w*wn;
}
}
}
if(flg==-1)
for(i=0;i<len;i++)
a[i].r/=len;
}
int main()
{
}
来看一道例题:
已知n根木棍的长度(n<=100000)(长度<=100000),从中选三根木棍,求使它们拼接成一个三角形的概率。
咋一看跟FFT半点关系都没有。
那我们先来看一看不用FFT的做法。
直接枚举三根木棍。。。显然TLE
先枚举两根木棍,通过三角形的条件,就可以知道另一根木棍的取值范围,二分查找满足条件的另一根有多少种选法。
O(n^2logn)。。。。还是TLE
但是第二种方法给了我们灵感。
我们可以用一个数组a[i]表示长度为i的木棍有a[i]根。
让它自己乘自己。
乘出来是个啥玩意儿???
首先,我们要把数组a看成一个系数为a[i],次数为i的多项式。(原本是木棍条数为a[i],长度均为i)
其次,当我们进行多项式乘法(也叫卷积)时
观察卷积后 x的次数,发现它是由次数为 j 的x与次数为(i-j)的x相乘而得
它对应的实际意义是:长度为 j 的木棍与长度为(i-j)的木棍相拼接后的长度
再观察 x的系数,发现它是由 a[j]*a[i-j] 而得
它对应的实际意义是:长度为 j 的木棍中选一根与长度为(i-j)的木棍中选一根相拼接的方案数
所以自己乘自己所得数组 b[i] 的意义就是选两根木棍,使它们长度和为 i 的方案数是 b[i]。
而卷积运算就可以通过FFT快速算出。
代码:
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
using namespace std;
#define N 400005
#define LL long long
const double PI=3.1415926535897932384626;
struct cp{
double r,i;
cp(){}
cp(double x,double y){r=x;i=y;}
cp operator + (const cp &t)const{return cp(r+t.r,i+t.i);}
cp operator - (const cp &t)const{return cp(r-t.r,i-t.i);}
cp operator * (const cp &t)const{return cp(r*t.r-i*t.i,r*t.i+i*t.r);}
}a[N],b[N],w,wn;
void change(cp a[],int len)
{
int i,j,k;
for(i=1,j=len/2;i<len-1;i++){
if(i<j) swap(a[i],a[j]);
for(k=len/2;j>=k;j-=k,k>>=1);
j+=k;
}
}
void fft(cp a[],int len,int flg)
{
int i,j,k;
for(i=2;i<=len;i<<=1){
wn=cp(cos(flg*2*PI/i),sin(flg*2*PI/i));
for(j=0;j<len;j+=i){
w=cp(1,0);
for(k=j;k<j+i/2;k++){
cp t=a[k];
cp u=a[k+i/2]*w;
a[k]=t+u;
a[k+i/2]=t-u;
w=w*wn;
}
}
}
if(flg==-1)
for(i=0;i<len;i++)
a[i].r/=len;
}
LL ans[N];
inline int getint()
{
char c;int num=0,flag=1;
while((c=getchar())<'0'||c>'9')if(c=='-')flag=-1;
while(c>='0'&&c<='9'){num=num*10+c-48;c=getchar();}
return num*flag;
}
int c[N],cd[N];
int main()
{
int T;
T=getint();
while(T--){
memset(c,0,sizeof(c));
int m,i;
m=getint();
for(i=1;i<=m;i++){
cd[i]=getint();
c[cd[i]]++;
}
sort(cd+1,cd+m+1);
int lena,lenb,len,n;
lena=lenb=cd[m]+1;
len=lena+lenb;n=1;
while(n<len)n<<=1;
for(i=0;i<lena;i++)b[i]=a[i]=cp((double)c[i],0);
for(i=lena;i<n;i++)b[i]=a[i]=cp(0,0);
change(a,n);change(b,n);
fft(a,n,1);fft(b,n,1);
for(i=0;i<n;i++) b[i]=a[i]*b[i];
change(b,n);fft(b,n,-1);
for(i=0;i<len-1;i++) ans[i]=(LL)(b[i].r+0.5);
len--;
for(i=1;i<=m;i++)ans[cd[i]*2]--;
for(i=0;i<len;i++)ans[i]>>=1;
for(i=1;i<len;i++)ans[i]=1ll*ans[i]+1ll*ans[i-1];
LL cnt=0,al=1ll*m*(m-1)*(m-2)/6;
for(i=1;i<=m;i++){
cnt=1ll*cnt+1ll*ans[len-1]-1ll*ans[cd[i]];
cnt=1ll*cnt-1ll*(m-1);
cnt=1ll*cnt-1ll*(m-i)*(m-i-1)/2;
cnt=1ll*cnt-1ll*(m-i)*(i-1);
}
printf("%.7lf\n",(double)cnt/al);
}
}
有了FFT,一些排列组合问题就可以转化为多项式运算来求解,曾经难以实现的操作都可以用FFT加速,FFT在解题上为我们开辟了一条全新的道路。(大雾)(其实就是生成函数的思维)
咕了4个月的博客终于写完了。。。










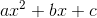
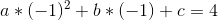
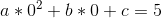
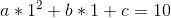
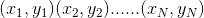
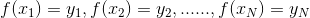
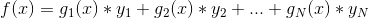
![g_i(x)=\prod_{j=1}^{N}[j!=i]*\frac{x-x_j}{x_i-x_j}](https://img-blog.csdnimg.cn/20181219151109646)
![f(x)=\sum_{i=1}^{N}y_i*\prod_{j=1}^{N}[j!=i]*\frac{x-x_j}{x_i-x_j}](https://img-blog.csdnimg.cn/20181219151230591)
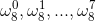
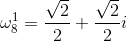
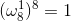
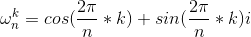
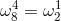
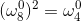
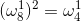
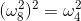
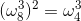
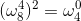
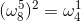
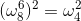
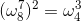
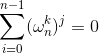













 1625
1625











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








