20200518 hz T1 矩阵求和【k次前缀和 → 路径数 → 组合数】

题目描述：

$n,m,Q\le 10^5,0\le k\le 10$

题目分析：

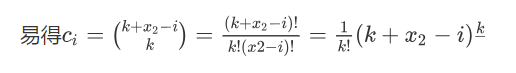
对于这个东西有两种处理方式：

方法一：预处理多项式系数

可以发现这就是一个关于$x_2$和$i$的二元多项式（看成是关于$x_2-i$的多项式也可以，写法会有点小区别），那么我们只需要对每个$k$预处理出 $x_2^u\ast i^v$ 的系数，然后维护$\sum a_i\ast i^k$，就可以枚举$u,v$带入$x_2$计算答案了。
修改复杂度$O(klogn)$，询问复杂度$O(k^2+klogn)$
Code：

#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
const int mod = 1e9+7;
int n,m,Q,a[maxn],b[maxn],F[11][11][11],pw[maxn][11];
int fac[maxn+10],inv[maxn+10],invf[maxn+10];
int C(int n,int m){return 1ll*fac[n]*invf[m]%mod*invf[n-m]%mod;}
struct BIT{
	int arr[maxn][11],s[11],lim;
	void upd(int x,int v){
		for(int i=0;i<=10;i++) s[i]=1ll*pw[x][i]*v%mod;
		for(int i=x;i<=lim;i+=i&-i) for(int j=0;j<=10;j++) arr[i][j]=(arr[i][j]+s[j])%mod;
	}
	void qsum(int l,int r){
		memset(s,0,sizeof s);
		for(int i=r;i;i-=i&-i) for(int j=0;j<=10;j++) s[j]=(s[j]+arr[i][j])%mod;
		for(int i=l-1;i;i-=i&-i) for(int j=0;j<=10;j++) s[j]=(s[j]-arr[i][j])%mod;
	}
}Ta,Tb;
int main()
{
	scanf("%d%d%d",&n,&m,&Q);
	
	for(int i=1,lim=max(n,m);i<=lim;i++) for(int j=pw[i][0]=1;j<=10;j++) pw[i][j]=1ll*pw[i][j-1]*i%mod;
	fac[0]=fac[1]=inv[0]=inv[1]=invf[0]=invf[1]=1;
	for(int i=2,lim=max(n,m)+10;i<=lim;i++) 
		fac[i]=1ll*fac[i-1]*i%mod,inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod,invf[i]=1ll*invf[i-1]*inv[i]%mod;
	
	F[0][0][0]=1;
	for(int k=1;k<=10;k++)
		for(int i=0;i<=10;i++)
			for(int j=0;j<=10;j++)
				F[k][i][j]=((i?F[k-1][i-1][j]:0)-(j?F[k-1][i][j-1]:0)+1ll*k*F[k-1][i][j])%mod*inv[k]%mod;
	
	Ta.lim=n,Tb.lim=m;
	for(int i=1;i<=n;i++) a[i]=1ll*(i-1)*m%mod,Ta.upd(i,a[i]);
	for(int j=1;j<=m;j++) b[j]=j,Tb.upd(j,b[j]);
	
	char op[3]; int x1,x2,y1,y2,k;
	while(Q--){
		scanf("%s%d%d",op,&x1,&y1);
		if(op[0]=='R') Ta.upd(x1,a[y1]-a[x1]),Ta.upd(y1,a[x1]-a[y1]),swap(a[x1],a[y1]);
		else if(op[0]=='C') Tb.upd(x1,b[y1]-b[x1]),Tb.upd(y1,b[x1]-b[y1]),swap(b[x1],b[y1]);
		else{
			scanf("%d%d%d",&x2,&y2,&k); int ans=0,r=0,c=0;
			Ta.qsum(x1,x2),Tb.qsum(y1,y2);
			for(int i=0;i<=k;i++) for(int j=0;j<=k;j++)
				r=(r+1ll*F[k][i][j]*pw[x2][i]%mod*Ta.s[j])%mod,
				c=(c+1ll*F[k][i][j]*pw[y2][i]%mod*Tb.s[j])%mod;
			ans=(1ll*r*C(k+y2-y1+1,k+1)+1ll*c*C(k+x2-x1+1,k+1))%mod;
			printf("%d\n",(ans+mod)%mod);
		}
	}
}

方法二：斯特林数展开下降幂