20200726 T3 树高【ETT(dfs序splay)维护同色边连通块】

题目描述

$n,m\le 10^5$，点的颜色范围为 $[1,30]$

题目分析

LCT可以维护黑白两色，黑点向父亲连边，实际连通块去掉根。但是整个连通块同时变色就不好整了。

用ETT（就是dfs序splay）维护边连通块，这样改变颜色的时候只会改变这条边与上下的连通性。用ETT是因为可以支持快速换子树，因为同一子树关键字是连续的。

初始时看做同一种颜色，按dfs序建树，splay点标对应原树点标。

一个边连通块为一棵以dfs序为关键字的 splay。

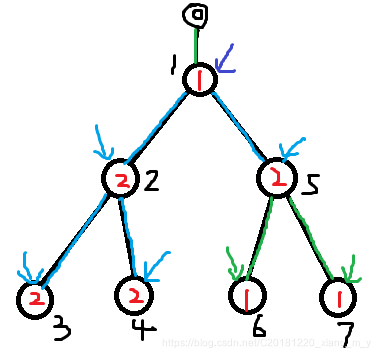
上图中同一种颜色的箭头指向的节点在同一棵 splay 中。

（link cut 之后实际上不同子树之间不一定是按原树dfs序排的，但是同一子树的关键字一定是连续的）

描述一下怎么操作（盯std盯了2h…）：

查询 $x$

$x=getroot(x)$

$getroot(x)$ 是找到 $x$ 所在边连通块的顶端，先找到 $x$ splay 中关键字最小的节点（一定是同层的某个同颜色顶端），得到 $x$ 与它的顶端的深度差，然后倍增往上跳。

上图中 $getroot(3)=2$

$rest=split(x)$

$split(x)$ 是将 $x$ 原树子树的边连通块与它所在的大连通块分离，返回值为分离之后的大连通块的 splay 的根。为了找到 $x$ 原树子树后面的关键字最小的点，平衡树中需要存 $ST,ED$ 表示子树中 $dfs$ 序的最小值和最大值。

上图中 $split(2)=5$

$printf(col[x],siz[x],mx[x]-dep[x]+1)$

$mx[x]$ 是 splay 维护的子树中的最大深度。

$if(rest\ne -1)merg{e}_0(rest,x)$

$merg{e}_0(x,y)$ 是将同层的两个同色边连通块合并。

改变 $x$ 的颜色为 $c$

首先 $splay(x,0)$，因为要把上面的标记传下来，才知道 $x$ 的 $color$

$if(col[x]==c)return;$

先分离出 $x$，$rest=split(x)$

$if(siz[x]>1)$ 断掉 $x$ 的后继与 $x$ 的连边（$x$ 不再与它

们同色），并更新 $son[x][col[x]]$ 为它的后继。

$son[x][c]$ 记录树上 $x$ 这个点接的颜色为 $c$ 的边连通块中 $x$ 的某个儿子。为了合并连通块时快速查找。还需要维护 $s[x]$ ，二进制第 $c$ 位表示 $son[x][c]$ 是否为 1，以及 $S[x]$ 表示 splay 子树中 $s$ 的或。$son[x][c]$ 只维护虚儿子，即不与 $x$ 颜色相同的 $c$ 处有值，因为同色的没有用，而且整个连通块变色的时候还要额外维护清零标记。

然后考虑合并 $x$ 与下面的连通块：$if(son[x][c])merg{e}_1(x,son[x][c])$

$merg{e}_1(x,y)$ 是将不同层（父子关系）的边连通块合并。

然后将 $son[x][c]$ 清零，$s[x]$ 去掉第 $c$ 位。（注意这些修改都要在 $x$ 为根的情况下做）

然后是 $x$ 与上面的连通块：$f=fa[x]$

$splay(f,0)$

$if(col[f]\ne col[x])$ 更改 $son[f][col[x]]$ 为 $rest$ 。分 $rest$ 是否为 $-1$ 讨论。

$if(col[f]\ne c)$ 将 $x$ 与 $son[f][c]$ 合并。分 $son[f][c]$ 的有无讨论。

$else$ 合并 $f,x$

改变 $x$ 同色连通块的颜色为 $c$

$x=getroot(x)$，如果颜色不用改直接 return。

$rest=split(x)$

给 $x$ 打上颜色 $c$ 的标记。

$travel(x,c)$：找到 $x$ 边连通块下方颜色为 $c$ 的点与其对应的父亲，根据 $S[x]$ 确定是否进子树，根据 $son[x][c]$ 确定。

找完之后依次将找到的连通块与 $x$ 合并。合并的总次数是 $O(n+m)$ 的。

与 $x$ 父亲的连通块的修改情况与单点修改一模一样。

---

呼~~~（描述完操作过了40min…）

尽管看起来很繁琐，实际上实现还要更繁琐，但是看了2h代码之后思路还是比较明了的。

Code：

#include<bits/stdc++.h>
#define maxn 100005
using namespace std;
int n,m,F[17][maxn],dep[maxn],st[maxn],ed[maxn],ln[maxn],tim;
int col[maxn],son[maxn][30];
vector<pair<int,int>>vec;
namespace ETT{
	int fa[maxn],ch[maxn][2],mx[maxn],ST[maxn],ED[maxn];
	int S[maxn],s[maxn],tag[maxn],siz[maxn];
	bool isc(int x){return ch[fa[x]][1]==x;}
	void upd(int x){
		siz[x]=siz[ch[x][0]]+siz[ch[x][1]]+1;
		mx[x]=max(dep[x],max(mx[ch[x][0]],mx[ch[x][1]]));
		ST[x]=min(st[x],min(ST[ch[x][0]],ST[ch[x][1]]));
		ED[x]=max(ed[x],max(ED[ch[x][0]],ED[ch[x][1]]));
		S[x]=s[x]|S[ch[x][0]]|S[ch[x][1]];
	}
	void paint(int x,int c){if(x) col[x]=c,tag[x]=c;}
	void pd(int x){if(~tag[x]) paint(ch[x][0],tag[x]),paint(ch[x][1],tag[x]),tag[x]=-1;}
	void pdpath(int x){if(fa[x]) pdpath(fa[x]); pd(x);}
	void rot(int x){
		int y=fa[x],z=fa[y],c=isc(x);
		if(z) ch[z][isc(y)]=x;
		fa[ch[y][c]=ch[x][!c]]=y, fa[ch[x][!c]=y]=x, fa[x]=z;
		upd(y);
	}
	void splay(int x,int goal=0){
		for(pdpath(x);fa[x]!=goal;rot(x))
			if(fa[fa[x]]!=goal) rot(isc(x)==isc(fa[x])?fa[x]:x);
		upd(x);
	}
	int findL(int x){while(ch[x][0]) x=ch[x][0]; return x;}
	int findR(int x){while(ch[x][1]) x=ch[x][1]; return x;}
	int Next(int x,int l,int r){
		if(!x) return 0;
		if(ST[ch[x][0]]<l||ED[ch[x][0]]>r) return Next(ch[x][0],l,r);
		if(st[x]<l||ed[x]>r) return x;
		return Next(ch[x][1],l,r);
	}
	int split(int x){
		int l=findR(ch[x][0]),r=Next(ch[x][1],st[x],ed[x]),rt;
		if(!l&&!r) rt=0;
		else if(!r) splay(l),fa[ch[l][1]]=0,ch[l][1]=0,upd(rt=l);
		else if(!l) splay(r),fa[ch[r][0]]=0,ch[r][0]=0,upd(rt=r);
		else splay(l),splay(r,l),fa[ch[r][0]]=0,ch[r][0]=0,upd(r),upd(rt=l);
		return splay(x),rt;
	}
	void merge0(int x,int y){
		splay(x),splay(x=findL(x)),splay(y),fa[ch[x][0]=y]=x,upd(x);
	}
	void merge1(int f,int x){
		splay(f),splay(x);
		if(ch[f][1]) splay(findL(ch[f][1]),f),fa[ch[ch[f][1]][0]=x]=ch[f][1],upd(ch[f][1]),upd(f);
		else fa[ch[f][1]=x]=f,upd(f);
	}
	void travel(int x,int c){
		if(son[x][c]) vec.push_back(make_pair(x,son[x][c])),son[x][c]=0,s[x]^=1<<c;
		if(S[ch[x][0]]>>c&1) travel(ch[x][0],c);
		if(S[ch[x][1]]>>c&1) travel(ch[x][1],c);
		upd(x);
	}
	int build(int l,int r,int ff){
		if(l>r) return 0;
		int mid=(l+r)>>1,i=ln[mid];
		fa[i]=ff,tag[i]=-1;
		if(l==r) return upd(i),i;
		ch[i][0]=build(l,mid-1,i),ch[i][1]=build(mid+1,r,i);
		return upd(i),i;
	}
}
using namespace ETT;
int fir[maxn],nxt[maxn];
void line(int x,int y){nxt[y]=fir[x],fir[x]=y;}
void dfs(int u){
	ln[st[u]=++tim]=u;
	for(int v=fir[u];v;v=nxt[v]) dep[v]=dep[u]+1,dfs(v);
	ed[u]=tim;
}
int getroot(int x){
	splay(x); int r=findL(x);
	for(int i=0,d=dep[x]-dep[r];d;d>>=1,i++) if(d&1) x=F[i][x];
	return splay(x),x;
}
void solve1(int x,int c){
	splay(x,0);
	int y=col[x]; if(y==c) return;
	int rest=split(x);
	if(siz[x]>1){//断掉 $x$ 的后继与 $x$ 的连边
		son[x][y]=findL(ch[x][1]),s[x]^=1<<y;
		fa[ch[x][1]]=0,ch[x][1]=0;
		upd(x),splay(son[x][y]);
	}
	col[x]=c;
	if(son[x][c]) merge1(x,son[x][c]),splay(x),son[x][c]=0,s[x]^=1<<c,upd(x);
	if(x!=1){
		int f=F[0][x];
		splay(f);
		if(col[f]!=y){
			if(!rest) son[f][y]=0,s[f]^=1<<y,upd(f);
			else splay(son[f][y]=findL(rest));
		}
		if(col[f]!=c){
			if(son[f][c]) merge0(x,son[f][c]);
			else son[f][c]=x,s[f]^=1<<c,upd(f);
		}
		else merge1(f,x);
	}
}
void solve2(int x,int c){
	x=getroot(x);
	int y=col[x]; if(y==c) return;
	int rest=split(x);
	paint(x,c);
	vec.clear(),travel(x,c);
//	for(int i=0;i<vec.size();i++) cout<<vec[i].first<<' '<<vec[i].second<<endl;
	for(int i=0;i<vec.size();i++) merge1(vec[i].first,vec[i].second);
	if(x!=1){
		int f=F[0][x];
		splay(f);
		if(col[f]!=y){//certainly.
			if(!rest) son[f][y]=0,s[f]^=1<<y,upd(f);
			else splay(son[f][y]=findL(rest));
		}
		if(col[f]!=c){
			if(son[f][c]) merge0(x,son[f][c]);
			else son[f][c]=x,s[f]^=1<<c,upd(f);
		}
		else merge1(f,x);
	}
}
void solve3(int x){
	x=getroot(x);
	int rest=split(x);
	printf("%d %d %d\n",col[x]+1,siz[x],mx[x]-dep[x]+1);
	if(rest) col[F[0][x]]==col[x]?merge1(F[0][x],x):merge0(rest,x);
}
int main()
{
	freopen("tree.in","r",stdin);
	freopen("tree.out","w",stdout);
	scanf("%d",&n);
	for(int i=2,x;i<=n;i++) scanf("%d",&x),line(x,i),F[0][i]=x;
	for(int j=1;j<=16;j++) for(int i=1;i<=n;i++) F[j][i]=F[j-1][F[j-1][i]];
	dfs(1);
	ST[0]=1e9,col[0]=30,build(1,tim,0);
	for(int i=1,x;i<=n;i++) scanf("%d",&x),solve1(i,x-1);
	scanf("%d",&m);
	for(int op,x,y;m--;){
		scanf("%d%d",&op,&x);
		if(op==3) solve3(x);
		else scanf("%d",&y),y--,op==1?solve1(x,y):solve2(x,y);
	}
}