每周刷题第一期

最新推荐文章于 2025-06-10 22:38:27 发布

星纭

最新推荐文章于 2025-06-10 22:38:27 发布

阅读量987

点赞数 39

分类专栏：刷题文章标签： c语言数据结构链表

本文链接：https://blog.csdn.net/CNDS_lili/article/details/138029307

版权

刷题专栏收录该内容

3 篇文章

订阅专栏

个人主页：星纭-CSDN博客

系列文章专栏：刷题

踏上取经路，比抵达灵山更重要！一起努力一起进步！

写题写题！！！

题目一：反转链表

题目出处：. - 力扣（LeetCode）

方法一：迭代

思路：头插法，在遍历这个链表的过程中，我们可以将每一个节点拿下来进行头插。比如将第一个节点进行头插后，到第二个结点时，进行头插这样第二个节点就在第一个节点前面了，遍历完了整个链表我们就完成了反转链表。

  struct ListNode {
      int val;
      struct ListNode *next;
  };

为了方便，我们可以先对其重命名一下。

typedef struct ListNode LTN;

这里我们需要用到带哨兵位的单链表，这样在哨兵位后面进行头插更加简单。

    LTN*phead = (LTN*)malloc(sizeof(LTN));

头插过程中需要的是将头插的这个节点的next指针指向phead的next,然后将phead指向头插的这个节点，这样就完成了头插。

在这个过程中，因为我们改变了要头插的这个节点的next指针，这样我们就找不到下一个指针了，所以我们需要再来一个指针指向下一个节点。

    LTN*cur = head;
    LTN*next= NULL;
    while(cur){
    	next = cur->next;
    	cur->next = phead->next;
    	phead->next = cur;
    	cur = next;
    }

最后我们只需要返回这个新链表的第一个节点即可。

思考一下上面的写法有没有什么问题？

其实是有的，我们在创建哨兵位的时候，并没有对其进行初始化，这样它的next指针指向的就是一个随机的地址，这样的指针是野指针，在打印完整链表的时候会造成非法访问。

完整代码：

 typedef struct ListNode LTN;
struct ListNode* reverseList(struct ListNode* head) {
    LTN*phead = (LTN*)malloc(sizeof(LTN));
    phead->next = NULL;
    LTN*cur = head;
    LTN*next= NULL;
    while(cur){
    	next = cur->next;
    	cur->next = phead->next;
    	phead->next = cur;
    	cur = next;
    }
    return phead->next;
}

方法二：递归

思路：这个函数的功能是反转链表，我们可以假设已经完成这个函数功能。

假设这个链表有k个节点，我们可以使用这个函数先反转后面k-1个节点。

这样这个链表就从n1->n2->n3->n4->n5->........->nk->NULL

变成了 n1->n2<-n3<-n4<-n5<-.........<-nk.

最后一步的实现就是让n2指向n1,也就是n1->next->next = n1,n1->next = NULL;

递归的思想就是将一个大问题分解成无数个相同的小问题，这样更易解决。我们再回过头来观察上面的方法，在深层次的递推时，就是先将最后一个节点指向倒数第二个节点，然后依次往前推。

    struct ListNode* newHead = reverseList(head->next);
    head->next->next = head;
    head->next = NULL;
    return newHead;

这个递归的结束条件是什么呢？

我们从倒数第二个节点来看，对于它来说它后面的节点根本不需要反转，是需要改变next的指向即可。这是因为它后面只有一个节点。也就是说只有一个节点就直接返回节点地址即可。

既然只有一个节点直接返回，那么没用节点呢？同理就是返回NULL了。

完整代码：

 typedef struct ListNode LTN;
struct ListNode* reverseList(struct ListNode* head) {
    if(head == NULL || head->next == NULL){
        return head;
    }
    LTN* newhead = reverseList(head->next);
    head->next->next = head;
    head->next = NULL;
    return newhead;
}

题目二：链表的中间节点

原题出处：. - 力扣（LeetCode）

方法一：

对于链表来说，它的缺点就是无法随机访问链表中的数据，必须要遍历整个数链表，而要找到中间节点，我们首先需要找到这个链表有多少个节点，然后就可以找到中间节点，先遍历一遍数组找到链表的节点个数N，然后第二次遍历时，遍历到N/2个节点即可。类似的，我们也可以将链表的值存放在一个数组中，通过数组的下标直接访问到中间值。这俩种方法的本质都是一样的。

这里就使用链表来解决。

如果链表有5个节点，也就是奇数个，N/2就是2.在头节点的基础上往后移动2个节点就是中间节点。

如果链表有6个节点，也就是偶数个，N/2就是3.在头节点的基础上往后移动3个节点就是中间节点的第二个。

均符合题目要求，所以我们就不必区分奇偶了。

typedef struct ListNode LTN;
struct ListNode* middleNode(struct ListNode* head) {
    int count = 0;
	LTN* cur = head;
	while(cur){
		++count;
		cur = cur->next;
	}
	count  = count / 2; 
	cur = head;
	while(count--)}{
		cur = cur->next;
	}
	return cur;
}

方法2：快慢指针

上面的方法是一个指针来解决的，我们不妨试一下双指针，当我们使用一个快指针每一次移动两步，而慢指针每一次移动1步，当遍历完链表后，这个慢指针指向的位置不就是中间节点了吗

假设快慢指针最开始都是指向head的

假设链表有5个节点，当fast指针指向最后一个节点的时候，slow指针指向中间节点。

假设链表有6个节点，当slow指针指向中间节点的时候，fast已经指向空了。

所以遍历链表的结束条件是当fast指针到最后一个节点或者已经为空停止。而最后一个节点也就是next指向空。

typedef struct ListNode LTN;
struct ListNode* middleNode(struct ListNode* head) {
    LTN*fast,*slow;
    fast = slow = head;
    while(fast && fast->next)
	{
		fast = fast->next->next;
		slow = slow->next;
	}
	return slow;
}

如果链表只有一个节点或者链表只有两个节点的情况，这个代码也是可以解决的。

题目三：环形链表的约瑟夫问题

题目出处：环形链表的约瑟夫问题_牛客题霸_牛客网

方法一：这个题的题目就告诉我们环形链表的约瑟夫问题，所以我们需要用到环形链表。

首先我们先来创建环形链表。

LTN* CreateCircle(int n);

注意：这道题有个问题，它是自带结构体的，不需要我们写了。

struct ListNode 
{
    int val;
    struct ListNode* next;
};

在创建新的链表的时候，我们首先需要动态开辟节点，所以我们先专门定义一个函数来完成这个功能。

typedef struct ListNode  LTN;
LTN* LTNBuyNode(int x){
	LTN* newnode  = (LTN*)malloc(sizeof(LTN));
	if(newnode == NULL){
		perror("malloc fail");
		exit(1);
	}
	newnode->val = x;
	newnode->next =NULL;
	return newnode;
}

为了方便控制这个链表，我们还是定义两个指针，头指针和尾指针。

	LTN*phead = LTNBuyNode(1);
	LTN*ptail =phead;

这个环状链表的第一个节点存储的数据是1，所以我们直接创建一个节点（里面存放数据1）即可，然后就是创建节点然后尾插。

LTN* CreateCircle(int n){
	LTN*phead = LTNBuyNode(1);
	LTN*ptail =phead;
	
	for(int i = 2;i <= n;i++){
		ptail = ptail->next = LTNBuyNode(i);		 
	}
	ptail->next = phead;
	
	return ptail;
}

因为已经有了1，所以循环从2开始直到n，结束循环，我们得到的是单链表，为了使其循环，还要将尾指针的next节点指向头节点。

细心读者肯定好奇为什么要返回尾指针，这里我们后面会讲。

这道题我们需要不断的遍历整个链表，直到链表只剩下一个节点。

假设我们使用cur指针从头节点开始，当遇到报号为m的节点的时候，我们就需要删除这个节点了，我们需要让cur上一个节点的next指针指向cur下一个节点，如果我们只是用一个指针，这是做不到的。

所以我们还需要一个prev指针指向cur的前一个节点。

cur是从phead开始的，它的前一个节点是ptail，如果我们在创建环形链表函数中返回phead，我们需要遍历整个数组才能找到ptail，所以我们直接返回ptail,使prev指向ptai，cur指向phead。这样我们在遇到报号m的节点时就可以释放了。

怎么来算这个报号呢？

我们需要专门的一个变量来计数，当cur每向下走一步就加1即可。

int ysf(int n, int m ) {
    // write code here
    LTN* prev = CreateCircle(n);
    LTN* cur = prev->next;
    int count = 1;
    while(cur->next != cur){
		if(count == m){
		prev->next = cur->next;
		free(cur);
		cur = prev->next;
		count = 1;
		}
		prev = cur;
		cur =cur->next;
		count++;
	}
	int ret = cur->val;
	free(cur);
	return ret;
}

因为cur从phead开始，已经是1了，所以count从1开始

当遇到m时，我们需要释放这个节点，然后将count置为1，因为cur已经来到下一个节点了。

因为还剩一个节点，我们只需要返回剩下一个人的编号，这个节点是我们需要自己释放的，避免内存泄漏。

如果不能理解，可以画图分析一下。

方法2：数学

假设f(n,m) 是总共n个人完，报号m的人退出的游戏的剩下一个人的编号。

接下来，我们分析f(n,m)与f(n-1,m)的关系

f(n,m)在完成一轮，淘汰一个人后，从淘汰的那个人开始重新计数，然后接着完成f(n-1.m)得到的位置应该和f(n,m)是一样的。

也就是如图所示：

那么我们就可以找到这里的关系了

f(n,m) = (f(n-1,m) + m % n) % n

我们直到是f(1,m) = 0的，因为最后一个一定会存活下来。

所以我们可以都得到以下关系

f(1,m) = 0

f(2,m) = (f(1,m) + m % 2) % 2

f(3,m) = (f(2,m) + m % 3) % 3

这里的公式是可以简化的，因为最终都要模上n所以f(n,m) = (f(n-1,m) + m) % n

int ysf(int n, int m ) {
    // write code here
    int ret = 0;//f(1,m)
    int i = 1;
    while(i <= n)
    {
		ret = (ret + m) % i;
		i++;
	}
	return ret + 1;
}

ret每经过一个循环，就会加1.直到f(n,m)

因为下标是从0开始，而题目是从1开始所以最后要加1.

此方法不好想到，第一个方法更偏向容易理解。

题目四：分隔链表

题目出处：. - 力扣（LeetCode）

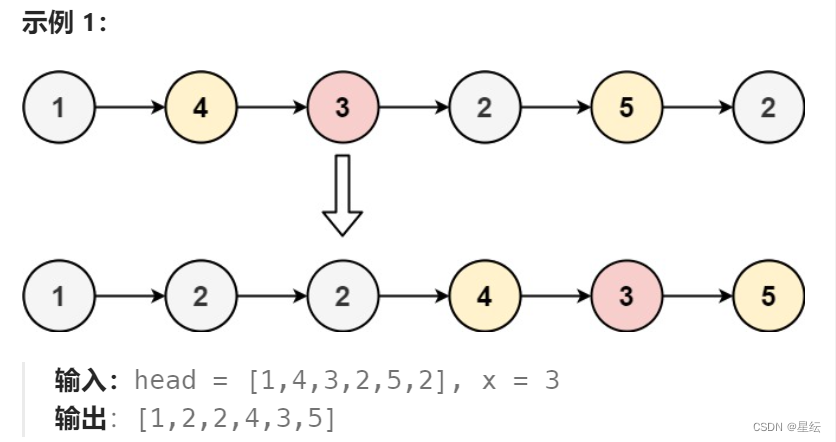
方法一：两个链表

思路：创建两个新的链表。分为小链表和大链表，将小于x节点插入小节点，大于的就插入大链表最后链接在一起。

这里的两个节点依然采用带哨兵位的链表，这样更方便我们管理链表，然后每一个链表采用两个指针分别管理每一个链表。

typedef struct ListNode ListNode;
struct ListNode* partition(struct ListNode* head, int x) {
	ListNode* greaterhead, * greatertail;
	ListNode* lesshead, * lesstail;
	lesshead = lesstail = (ListNode*)malloc(sizeof(ListNode));
	greatertail = greaterhead = (ListNode*)malloc(sizeof(ListNode));
	lesshead->next = lesstail->next = NULL;
	greatertail->next = greaterhead->next = NULL;
}

这里可以思考一下为什么要把头节点的next指针给初始化为NULL?后面再讲

在我们创建完两个链表之后接下来就是插入节点了，这里我们采用尾插，因为有尾指针的存在更加方便，有人可能想问为啥不只使用一个头指针然后头插，因为，这样头插的链表节点的next指针并不是指向NULL的，我们就不能知道这个链表从哪里结束了，这也说明了为什么要使用两个指针。

    ListNode* cur = head;
    while (cur) {
        if (cur->val < x) {
            lesstail->next = cur;
            lesstail = lesstail->next;
        }
        else {
            greatertail->next = cur;
            greatertail = greatertail->next;
        }
        cur = cur->next;
    }

在头插完了之后就需要连接两个链表了。

   lesstail->next = greaterhead->next;

我们再思考一下这里我们的代码结束没有？

肯定是没有的，因为这个链表的大链表的尾结点的next指针并不是指向NULL,他可能还指向在原链表的下一个节点，这肯定是不行的。所以我们就需要将它置为NULL.

    greatertail->next = NULL;

到这里其实就差不多了，我们再回过头来看开始的问题，为什么要给头节点初始化？如果不初始化，会有什么问题？

答案是：如果不初始化会造成野指针，非法访问。

如果我们不初始化，那么它的值节点中的成员变量就是随机值，而我们回过头来看我们写代码的顺序，我们可以发现，如果大链表中除了头节点没有其他节点，那么在 lesstail->next = greaterhead->next;lesstail的next指针指向一个随机的空间，这是不行的。

如何解决呢？

这里就是为什么我们要开始进行初始化了，头节点中的val进不进行初始化无所谓，因为即使是随机值也不影响，它的数据对我们来说没有用，但是节点的next指针就非常重要了。

还有一种方法就是先将greatertail->next置为NULL,也可以解决问题，但是这样的方法在我们思考时难以想到。

最后养成好习惯，动态申请的空间要释放，

    ListNode* ret = lesshead->next;
    free(lesshead);
    free(greaterhead);
    greatertail = lesstail = NULL;
    return ret;

完整代码：

typedef struct ListNode ListNode;
struct ListNode* partition(struct ListNode* head, int x) {

    ListNode* greaterhead, * greatertail;
    ListNode* lesshead, * lesstail;
    lesshead = lesstail = (ListNode*)malloc(sizeof(ListNode));
    greatertail = greaterhead = (ListNode*)malloc(sizeof(ListNode));
    lesshead->next = lesstail->next = NULL;
    greatertail->next=greaterhead->next = NULL;

    ListNode* cur = head;
    while (cur) {
        if (cur->val < x) {
            lesstail->next = cur;
            lesstail = lesstail->next;
        }
        else {
            greatertail->next = cur;
            greatertail = greatertail->next;
        }
        cur = cur->next;
    }
    lesstail->next = greaterhead->next;
    greatertail->next = NULL;


    ListNode* ret = lesshead->next;
    free(lesshead);
    free(greaterhead);
    greatertail = lesstail = NULL;
    return ret;
}

新建节点要初始化，否则是随机值。

题目五：合并两个有序数组讲解

原题出处： . - 力扣（LeetCode）

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {

}

将两个非递减顺序的数组进行合并，但是最后的数组仍然要非递减，也就是递增。

方法一：直接合并再使用qsort函数进行排序

因为这道题的nums1数组的大小是包含nums1Size和nums2Size的，只需要将nums链接在数组nums1的有效数据的后面即可。

	for (int i = 0; i < n; i++) {
		nums1[i + m] = nums2[i];
	}

此时的nums1数组的顺序并不是递增的，然后我们再使用qsort 进行排列，因为qsort函数的底层是快速排列，速度更快，这道题并没有时间复杂度的限制，当然也可以使用冒泡排序。

这里不过多讲解qsort函数的使用，有问题可以私信。

最后完成qsort的第三个参数函数就可以了

int cmp(const void* p1, const void* p2) {
	return *(int*)p1 - *(int*)p2;
}

void merge(int* nums1, int nums1Size, int m, int* nums2, int nums2Size, int n) {
	for (int i = 0; i < n; i++) {
		nums1[i + m] = nums2[i];
	}
	qsort(nums1,m + n,sizeof(nums1[0]),cmp);
}

方法2：双指针

使用双指针的话，这里我们可以再创建一个数组，使用两个指针分别指向两个数组的头部，然后比较谁更小，将小的拿到新的数组中，指针加1，直到完成遍历。

但是这样的方法还可以优化，如何在不使用新数组的情况下，完成这道题呢。

我们使用新数组的原因是当我们直接在nums1中移动数据的时候，可能会覆盖数据。

可是如果我们使用逆向双指针，就不会了，因为在nums1中后面的数据都是0，这些不是有效的数据，我们不用考虑数据被覆盖的问题。

	int end1 = m - 1;//指向第一个数组的有效数据最后一个
	int end2 = n - 1;//指向第二个数组的有效数据最后一个
	int newend = nums1Size - 1;//指向新的数组
	while (end1 >= 0 && end2 >= 0) {
		if (nums1[end1] > nums2[end2]) {
			nums1[newend] =  nums1[end1];
			newend--;
			end1--;
		}
		else {
			nums1[newend] = nums2[end2];
			end2--;
			newend--;
		}
	}

为了防止越界访问，while循环的条件是两个end都要大于等于0。这样写有问题吗？

有问题

在最后跳出循环的时候，有两种情况，第一种是

end2小于0了，此时数组2中的数据全部都在nums1中了，此时是没有问题的。

第二种情况是end1先为负，此时nums2中的数据并没有移动完，如果我们直接返回此时就是错误的了。所以我们在最后应该再判断一下。

 	while (end2 >= 0) {
		nums1[end2] = nums2[end2];
		end2--;
	}

如果end1先为负，我们再把数组2中剩余的数据移到数组1中即可。

最后考虑一个问题，如果数组1中没有有效数据怎么办？

nums2就是我们要得到的数组，这个代码是可以解决这个问题，因为我们最后把数组2的数据移动到了数组1中。

同理如果数组2没有数据呢？

我们可以在开头加一个判断，如果n为0直接结束函数。

if(n == 0)
    return;

这样就不用后续了，但是不加也可以。

题目六：移除链表元素

原题出处：. - 力扣（LeetCode）

方法一：迭代

我们可以新创建一个链表，然后将不等于val的节点拿下来进行尾插，这样的方式更加简易，只需要遍历整个链表即可。

我们首先使用一个指针cur来遍历原链表，来获取不等于val的节点。

如果cur的next等于val就跳过这个节点，如果不等于val就尾插，直到当cur等于NULL,这时候就遍历完了整个数组。

然后再使用两个指针分别指向新链表的开头和末尾。

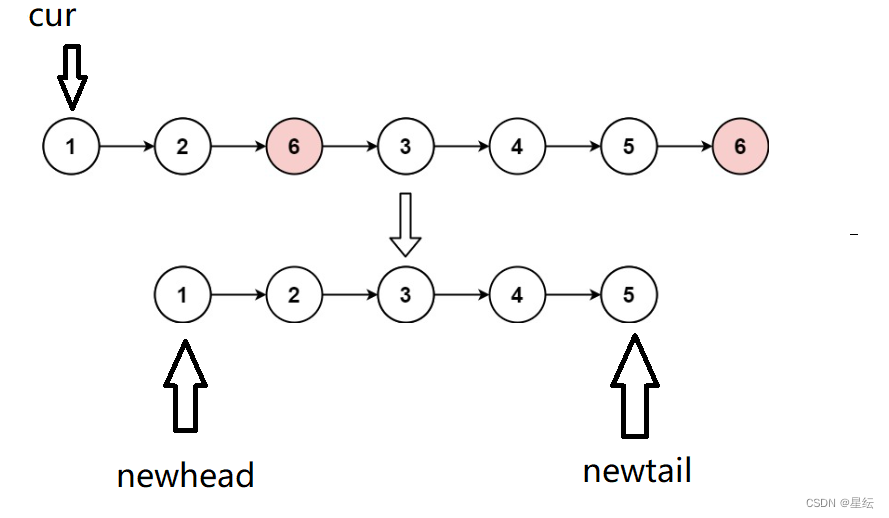
struct ListNode* removeElements(struct ListNode* head, int val) {
	struct ListNode* newhead = NULL,*newtail = NULL,*cur = head;
	while(cur != NULL) {
		if (cur->val != val) { 
			if (newhead == NULL) {
				newhead = newtail =  cur;
			}
			else {
				newtail->next = cur;
                newtail = newtail->next;
			}
		}
		cur = cur->next;
	}
    if(newtail)
        newtail->next = NULL;
	return newhead;
}

最开始进行尾插的时候，因为newhead和newtail都是NULL,这时候并不是尾插而是让newhead和newtail指向这个节点。

为了避免这个情况，我们也可以使用带有哨兵位的链表来解决这个问题。

struct ListNode* removeElements(struct ListNode* head, int val) {
	struct ListNode* guardHead = malloc(sizeof(struct ListNode));
	guardHead->next = head;
	struct ListNode* cur = guardHead;
	while (cur->next != NULL) {
		if (cur->next->val == val) {
			cur->next = cur->next->next;
		}
		else {
			cur = cur->next;
		}
	}
	struct ListNode* ret = guardHead->next;
	free(guardHead);
	return ret;
}

但是由于这个哨兵位是我们malloc的，最后离开函数一定要释放，否则会造成内存泄漏。

这个方法是有点缺陷的，如果这些节点是使用动态内存开辟的，我们就没有释放这些节点，但是这个方法是满足题目条件的。

方法二：递归

链表的定义是具有递归的性质，因此链表的题目是可以使用递归解决的

首先我们明白这个函数的功能是删除这个链表中等于val的元素的，那么我们可以对除开第一个节点的对后面的节点使用这个函数，得到的返回值就是就是后面的所有的节点就没有等于val的了。

    head->next = removeElements(head->next,val);

这样我们head->next后面的节点都没有了等于val的。

然后由于我们没有判断第一个节点是否等于val，此时我们就可以使用三目操作符来判断了。

 return head->val == val ? head->next : head;

如果头节点是等于val的，我们就返回head->next,这样我们就删除了所有等于val的节点。如果不等于val就直接返回head即可。

但是这里还有一个问题就是如果head节点是空，这样就会非法访问空节点了，所有我们还要判断是否是空节点。

struct ListNode* removeElements(struct ListNode* head, int val) {
    if(head == NULL){
        return head;
    }
    head->next = removeElements(head->next,val);
    return head->val == val ? head->next : head;
}

题目七：轮转数组

题目链接：. - 力扣（LeetCode）

题目：给定一个整数数组 nums，将数组中的元素向右轮转 k 个位置，其中 k 是非负数。

示例：

void rotate(int* nums, int numsSize, int k) {
    
}

nums数组的地址，numsSize是数组的大小（方便起见，后面用n代指），k直的是向右轮转的次数。

方法一：使用额外数组

思路：我们先创建一个新的数组，将原数组中的数根据k计算出在轮转之后的位置，然后放置在新数组中，遍历整个数组，直到完成所有元素的放置，最终将新数组的内容依次还给原数组。

假设这里有一个大小为5的数组，如果我们要轮转3次，那么第4个位置上的数就会到第二个位置上去。也就是第i个位置上的数会到第(i+k)%numsSize位置上去。直到了这个也就掌握了这个方法的关键所在。

然后我们知道轮转numsSize次，等于没有轮转，所以当k的值大于numsSize时，我们可以取余一次。

代码：

void rotate(int* nums, int numsSize, int k) {
	int newArr[numsSize];//创建一个同类型的数组
    //创建一个新的数组
    int k = k % numsSize;
	for (int i = 0; i < numsSize; i++) {
		newArr[(i + k) % numsSize] = nums[i];
        //根据k来得到旋转后的位置；
	}
	for (int j = 0; j < numsSize; j++) {
		nums[j] = newArr[j];//将新数组的数还给原数组。
	}
}

方法二：三次逆置法/翻转数组法

假设这里有五个数，将其向右轮转2。

我们会发现第三次就是我们所要的结果，那么是如何翻转的呢？

第一次是将后k个数逆置，第二次是将前n-k个数进行逆置，第三次是将整体进行逆置。这样就实现了k次轮转。

代码：

void reverse(int *a,int left,int right){
    while(left<right){
        int tmp = a[right];
        a[right] = a[left];
        a[left] = tmp;
        left++;
        right--;
    }
}
void rotate(int* nums, int numsSize, int k) {
    k %= numsSize;

    reverse(nums,numsSize - k,numsSize - 1);//逆置后面k个数
    reverse(nums,0,numsSize - k - 1);//逆置前面n-k个数
    reverse(nums,0,numsSize - 1);。。整体逆置

}

这种方法第一次做难以想到，这与数学有关。

方法三：memcpy函数

我们可以使用memcpy函数解决这道题。

我们首先分配一个临时内存，我们将原数组的后k个数，拷贝到这个临时空间中，再将前n-k数拷贝到tmp+k的地方，这样我们就实现了数组的轮转，只不过不是原数组，最后我们再将tmp拷贝到原数组中就完成了。

void rotate(int* nums, int numsSize, int k) {
    k = k % numsSize;
    int  *tmp = (int*)malloc(sizeof(int)*numsSize);
    memcpy(tmp+k,nums,sizeof(int)*(numsSize-k));
    memcpy(tmp,nums+numsSize-k,sizeof(int)*k);
    memcpy(nums,tmp,sizeof(int)*numsSize);
    free(tmp);
    tmp = NULL;
}