单位对角矩阵的特性分析

     矩阵可以理解为向量。所谓向量，就是在一个正交坐标系下，有大小和方向的量。二维/三维矩阵的向量描述，可以用几何图形表示。

      例如以下二维矩阵：

           D=

      可以用图一表示：

                           图一             

     α=a11i+a12j;

     β=a21i+a22j;

     假如A 是两个三维向量（坐标系是xyz）,B是二维向量（坐标系是XY）,这两个矩阵的乘积，可以理解为坐标系的变换。

            

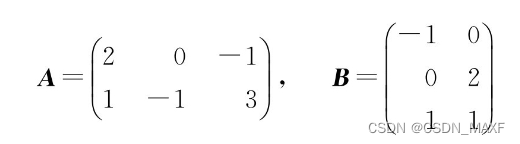
       A与B的乘积，可以看成是把三维向量转化为二维向量。B是转换公式，新的坐标系是XY。相乘的结果，是两个二维向量。

从这个角度来考虑：

1. 转换前后，向量的个数是没有变化的，即：变化前后的向量个数是一样的。
2. 向量的个数，由第一个矩阵的行数确定。
3. 向量的维数是可以变化的。变换前后，不一定要求维数是一样的。
4. 矩阵的行代表向量的维数。第一个矩阵行的元素个数，代表原始坐标系的维数；第二个矩阵行的元素个数代表目标坐标系的维数。第二个矩阵的行数，要等于原始坐标系的维数。
5. 第二个矩阵的大小，由原始坐标系和目标坐标系决定，与向量的个数无关。
6. 如果两个矩阵A、B的乘积存在，则矩阵B、A的乘积不一定存在。因为A矩阵包含向量的个数，不是单纯的坐标系转换。

任何单位对角矩阵（即对角线上的元素为1，其他元素为0），与相同大小的矩阵相乘，结果是这个矩阵自身。可以理解为，单位对角矩阵与变换矩阵的乘积，就是变换矩阵本身。

图二是用Matlab实现的一个单位对角矩阵，对角线上的点为1，其余的点位0；

                                     图二

 图三是一张正常的彩色图片的灰度图经过图形转换的前后对比。变换方式是：

tform=maketform('projective',[1 0 0;.5 2 0;0 0 1])

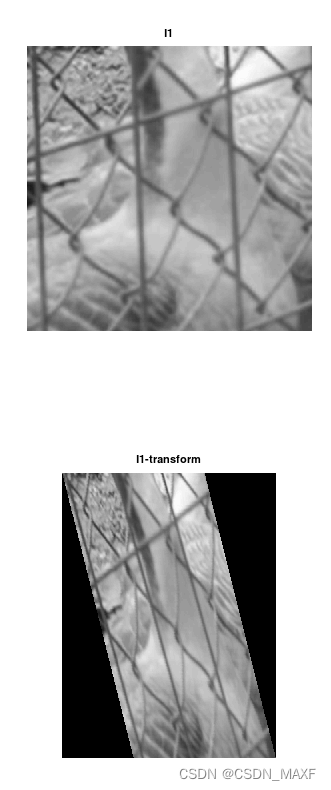
           图三

  图四是单位对角矩阵经过相同变换后的图形。

          图四

  图五是单位对角矩阵变换后的矩阵数据截图（原始数据为对角线上的值为255，其余为0）。

图五

图六是单位对角矩阵变换前后每个像素点的形状对比。

图六

单位对角矩阵的变换结果，就是变换矩阵自身。所以，可以看到该变换的特点：

1. 输出矩阵的行和列的大小有变化（有插值）；
2. 在矩阵的对角线上的值有变化，并且周围3个像素的值有相应变化。

END