递归思想入门-回归解决问题最简单的版本

最新推荐文章于 2025-03-21 22:23:28 发布

码拉松

最新推荐文章于 2025-03-21 22:23:28 发布

阅读量1.7k

点赞数 38

分类专栏：经验分享文章标签：算法面试

本文链接：https://blog.csdn.net/CSDN_WYL2016/article/details/143066975

版权

经验分享专栏收录该内容

75 篇文章

订阅专栏

前言

递归思维实质上体现了一种逆向推理的逻辑方式，即从最终结果回溯至初始条件。在一步步的倒推过程中，我们发现每一步要解决的问题本质上都是一样的。通过将复杂的大问题分解为多个相似的小规模子问题，进而揭示出解决问题的最基本单元，为寻找最简化的解决方案提供了有效途径。

接下来，本篇文章通过几个例子带你感受下利用递归思维解决问题的魔力。

逻辑题

狼吃羊

有5只灰太狼和1只喜羊羊被困在了孤岛上，狼可以选择吃草或者吃羊，只能同时有一只狼吃羊，其他的狼当观众。如果有狼选择吃羊，那么吃完以后这只灰太狼会变成美羊羊，剩下的狼可以继续选择吃它或吃草。假设每只狼都很聪明，并且每只狼都贪生怕死，那么喜羊羊会被灰太狼吃掉吗？

如果 5 只灰太狼的情况太复杂，我们可以先假设只有 1 只灰太狼，当只有 1 只灰太狼和 1 只喜羊羊时，喜羊羊一定会被吃掉。

当我们知道 1 只灰太狼和 1 只喜羊羊存在时的选择后，我们就可以假设有 2 只灰太狼和 1 只喜羊羊的情况，如果此时选择吃羊，那么吃掉后情况将回到 1 只灰太狼和 1 只喜羊羊的情况，而在这种情况下，我们已经知道喜羊羊一定会被吃掉，所以当有 2 只灰太狼和 1 只喜羊羊时，应该选择不吃。

最终，按照这种思路，我们发现最本质的问题就是在问当 1 只狼和 1 只羊同时存在时做出的选择。

狼的数量	羊的数量	选择
1	1	吃
2	1	不吃	如果此时有一只狼吃了羊，那么整个局面就会变成了1只狼和1只羊的情况，而前一步已经分析出在1只狼和1只羊的情况下，羊会被吃，所以聪明狼此时应该选择不吃。
3	1	吃	同理，3只狼中有一种吃了羊之后，局面就变成了2只狼和1只羊的情况，根据前一步分析得出，在2只狼和1只羊的情况下，羊不会被吃，所以聪明狼此时会争先恐后的把羊吃掉。

以此类推，最终结论就是奇数只狼时一定会把羊吃掉，偶数只狼时则不会吃。

舞会

有一群人开舞会，每人头上都戴着一顶帽子．帽子只有黑白两种颜色，黑的至少有一顶．每个人都能看到其它人帽子的颜色，却看不到自己的．主持人先让大家看看别人头上戴的是什么帽子，然后关灯，如果有人认为自己戴的是黑帽子，就拍手．第一次关灯，没有声音．于是再开灯，大家再看一遍，关灯时仍然鸦雀无声．一直到第三次关灯，才有劈劈啪啪手的声音响起．请问有多少人带的是黑帽子？

如果你以前学会了狼吃羊的问题，那么本题舞会带帽子的问题也可以采用相同的方式来解决。比如先假设 1 人带黑帽子会是什么样的情况，再假设 2 人、3 人带黑帽子的情况之后尝试找到问题的本质。

你可以先尝试分析。

以下，是具体分析过程。

假设舞会有10个人参加。如果带帽子的是 1 人，那么带白帽子的就有 9 人，按照此思路开始分析。

带黑帽子的数量	带白帽子的数量
1	9	戴黑帽的人一看，其他9个人戴的都是白的，所以第一关灯时他一定会拍手
2	8	两个戴黑帽的人第一次看到的都是1个黑帽和8个白帽，因为此时无法判断自己戴的是黑帽还是白帽，所以第一次关灯时没人拍手，因为第一次关灯时没人拍手，就证明了肯定不是1黑9白的情况，那就只剩2黑8白的情况了，所以第二次关灯，两个人就都拍手了。
3	7	三个戴黑帽的人第一次看到的都是2个黑帽和7个白帽，此时三个人都无法判断自己戴的是黑帽还是白帽，所以第一次关灯没人拍手，同理，第二次关灯也不会有人拍手，因为根据前面的推论，只有在看到是1黑8白时，第二次关灯才会有人拍手，此时三个人就都明白了，既然不是2黑8白的情况，那就一定是3黑7白了，所以第三次关灯时，三个人就都拍手了。

以此类推，最终结论就是第几次关灯有人拍手，就有多少人戴黑帽子。

数学游戏

报数

报数游戏是一个非常经典的需要通过逆向思维来思考获胜方式的小游戏一般 2、3 年级的小朋友就可以参与了，玩法大致如下：

有甲、乙两人从 1 开始轮流报数，每人每次可以报 1 个数或 2 个数，谁先报到 21 谁就赢。如果想要必赢，是先报还是后报？

这个游戏只要多玩几次就能发现，要想先报到 21，就等于要先报到 18，同理，要想先报到 18，就等于要先报到 15。最终，不难发现，想要必赢就得确保每次可以报到 3 的倍数的数。

所以，如果是甲先报，无论是报 1 还是报 2，接下来乙都可以一直报到 3 的倍数，所以当都清楚游戏规则的前提下，谁先报谁必输！

但如果是要求谁先报到 20 谁就赢呢？20 的前一个制胜数是 17，再往前以此是 14,、11、8、5、2，所以，此时就变成了谁先报谁必赢了！

汉诺塔

法国数学家爱德华·卢卡斯曾编写过一个印度的古老传说：在世界中心贝拿勒斯（在印度北部）的圣庙里，一块黄铜板上插着三根宝石针。印度教的主神梵天在创造世界的时候，在其中一根针上从下到上地穿好了由大到小的64片金片，这就是所谓的汉诺塔。不论白天黑夜，总有一个僧侣在按照下面的法则移动这些金片：一次只移动一片，不管在哪根针上，小片必须在大片上面。僧侣们预言，当所有的金片都从梵天穿好的那根针上移到另外一根针上时，世界就将在一声霹雳中消灭，而梵塔、庙宇和众生也都将同归于尽。

汉诺塔问题可以这样分析：

如果柱子上只有 1 个盘子（n = 1），那直接将 A 移动到 C 即可。

在这里插入图片描述

如果有 2 个盘子（n = 2），则先将最上面的盘子移动到 B，再把下面的盘子移动到 C，最后把 B 上面的盘子移动到 C 即可。

在这里插入图片描述

如果有 3 个盘子（n = 3）呢？实际上要解决的就是，将最上面的两个盘子移动到 B 柱子上，再把下面的盘子移动到 C，最后把 B 上面的盘子移动到 C ，这个过程本质上和有 2 个盘子时是一样的。

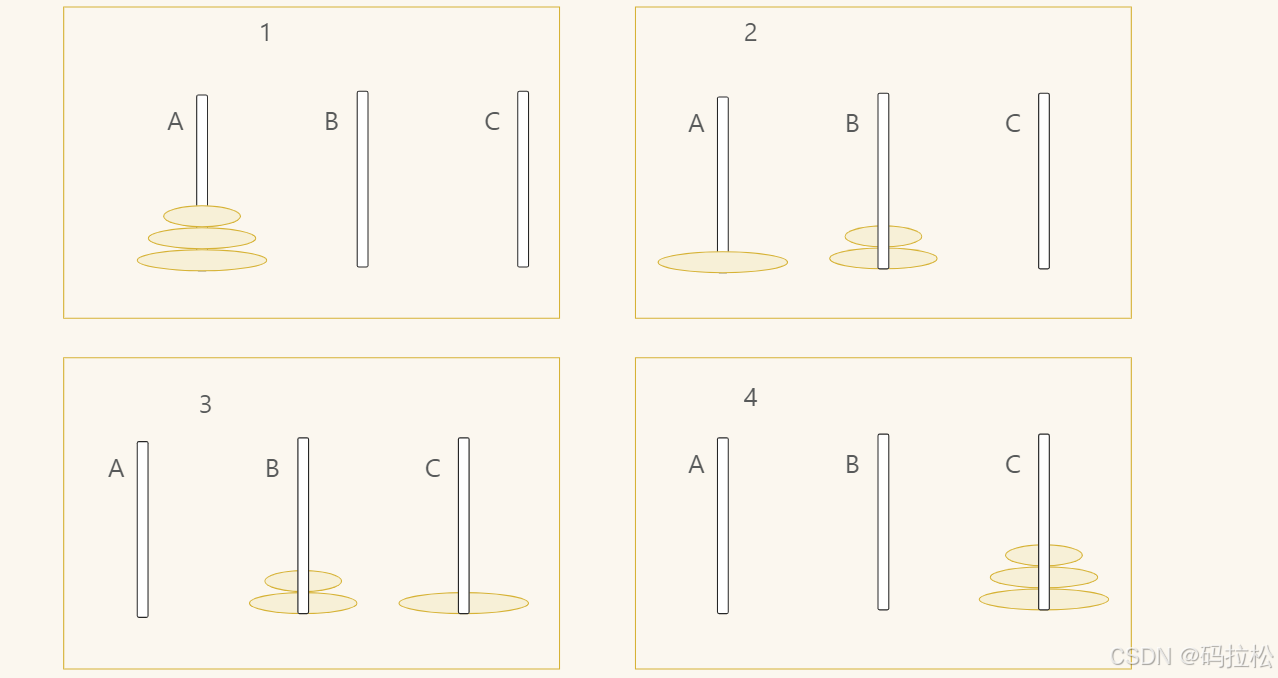
在这里插入图片描述

而如何能顺利做到第二步呢？前面说了，我们完全可以把它当做只有两个盘子的情况，然后目标是从 A 柱移动到 B 柱的过程，以及再从B柱移动到C柱的过程。

所以，如果移动 n 个盘子需要 $f (n)$ 步，则： $f (n) = 2 * f (n - 1) + 1$ 步。

且我们通过实际操作已经知道 $f (1) = 1$ ， $f (2) = 3$ ，所以， $f (3) = 7$ 。

进一步观察我们还能发现移动次数实际上等于：$ 2^n - 1$，所以要移动 64 个盘子，哪怕一次只需要 1 秒，也需要 5800 多亿年，要知道地球存在至今也不过 45 亿年。

斐波那契数

斐波那契数列如下： $0, 1, 1, 2, 3, 5, 8, 13, 21......$ 数列由 0，1 开始，之后的每一项数字都是前面两项数字的和。

所以，如果要求该数列的第 10 项，也就等于求该数列的第 9 项和第 8 项之和，同理，如果要求第 9 项，就是要求第 8 项和第 7 项之和，一直这样推下去，直到求第 1 项和第 2 项之和。

递推公式： $F (n) = F (n - 1) + F (n - 2)$ ，其中 $n > 1$

斐波那契数列最早是由数学家是斐波那契在《算经》一文中记载的有关“兔子繁殖”问题而来的，该问题大致如下：

如果每对兔子（一雄一雌）每月能生殖一对小兔子（也是一雄一雌），每对兔子前 2 个月没有生殖能力，但从第三个月以后便能每月生一对小兔子。假定这些兔子都没有死亡现象，那么从第一对刚出生的兔子开始，12 个月以后会有多少对兔子呢？

第一个月：只有 1 对兔子（第 1 个月出生的）。

第二个月：只有 1 对兔子（第 1 个月出生的）。

第三个月：这对兔子（第 1 个月出生的兔子）生了 1 对兔子（第 3 个月出生的兔子），此时有 2 对兔子了。

第四个月：第一对兔子（第 1 个月出生的）继续生了一对兔子（第 4 个月出生的兔子），此时有 3 对兔子了。

第五个月：第一对兔子（第 1 个月出生的）继续生了一对兔子（第 5 个月出生的兔子），第二对兔子（第 3 个月出生的）也生了他们的第一对兔子（第 5 个月出生的兔子），所以此时应该有 3 + 2 = 5 对兔子。

第六个月：第一对兔子（第 1 个月出生的）继续生了一对兔子（第 6 个月出生的兔子），第二对兔子（第 3 个月出生的）继续生了一对（第 6 个月出生的兔子），第三对兔子（第 4 个月出生的兔子）也生了他们的第一对兔子（第 6 个月出生的兔子），所以此时应该有 5 + 3 = 8 对兔子。

第七个月：第一对兔子（第 1 个月出生的）继续生了一对兔子（第 7 个月出生的兔子），第二对兔子（第 3 个月出生的）继续生了一对（第 7 个月出生的兔子），第三对兔子（第 4 个月出生的兔子）继续生了一对（第 7 个月出生的兔子），第四对兔子（第 5 个月出生的兔子，注意在第 5 个月出生了 2 对兔子），所以第四对兔子，一共生了 2 对（第 7 个月出生的兔子），所以此时应该有 8 + (3 + 2) = 13 对兔子。

最终，算下来就这样的队列就被定义为了斐波那契数列。神奇的是斐波那契数列不仅存在很多数学问题之中，就连大自然界也存在着这样的奇妙构造，比如有些植物的树枝、鲜花的花瓣、蜂房的结构等。

算法题

在算法题中，有些问题的处理也特别适合通过递归的方式来解决，比如树、回溯等。接下来，我会列举leetcode上几道经典的算法题。

本文不讲解具体算法实现分析，只意在普及递归应用思想，对算法有兴趣的可专门进行研究。

先尝试计算前面的两道数学题：斐波那契数列与汉诺塔

斐波那契数列

在这里插入图片描述

class Solution {
    public int fib(int n) {
        if(n == 0){
            return 0;
        }
        if(n == 1){
            return 1;
        }
        return fib(n - 1) + fib(n - 2);
    }
}

汉诺塔

在这里插入图片描述

class Solution {
    public void hanota(List<Integer> A, List<Integer> B, List<Integer> C) {
        move(A.size(), A, B, C);
    }

    public void move(int n, List<Integer> A, List<Integer> B, List<Integer> C){
        if(n == 1){
            // 当只有1个盘子时，直接移动，从A到C
            C.add(A.remove(A.size() - 1));
            return;
        }
        // 当非1个盘子时，我们的目标是将n-1个盘子从A移动到B，此时C是我们的辅助柱子
        move(n - 1, A, C, B);
        // 当完成n-1个盘子移动时，直接将第n个盘子从A移动到C
        C.add(A.remove(A.size() - 1));
        // 最后，再将B柱子上的n-1个盘子移到C柱子上，此时A柱子是我们的辅助柱子
        move(n - 1, B, A, C);
    }
}

树

几乎所有树的问题都可以通过递归来解决，这主要是由树的这种数据结构所决定的。

树的前中后序遍历

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> ans = new ArrayList<>();
        dfs(root, ans);
        return ans;
    }

    public void dfs(TreeNode root, List<Integer> ans){
        if(root == null){
            return;
        }
        // 如果ans.add(root.val)放在这处理，就是前序
        ans.add(root.val);
        dfs(root.left, ans);

        // 如果ans.add(root.val)放在这处理，就是中序
        // ans.add(root.val);
        
        dfs(root.right, ans);

        // 如果ans.add(root.val)放在这处理，就是后序
        // ans.add(root.val);
    }
}

二叉树的最大深度

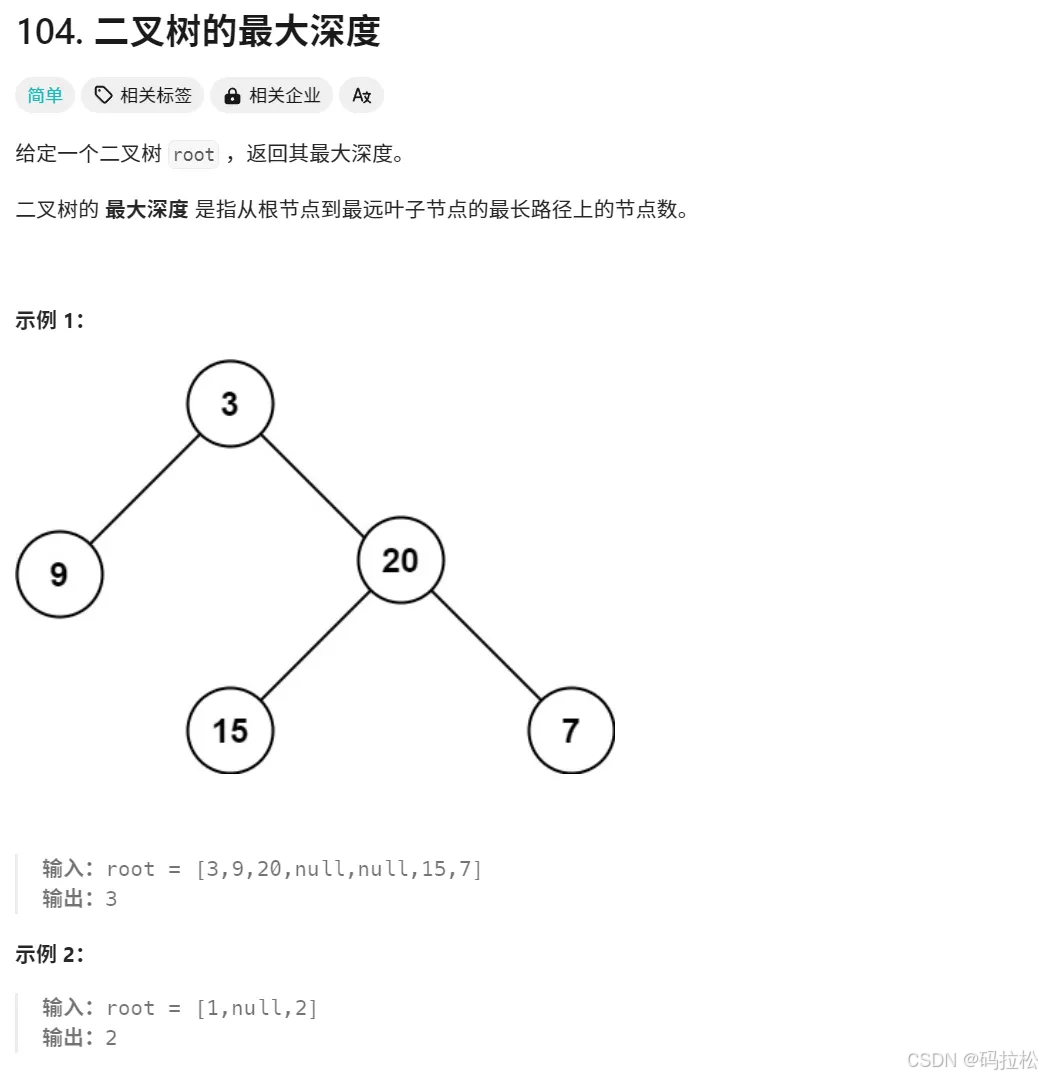
在这里插入图片描述

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
        if(root == null){
            return 0;
        }
        int left = maxDepth(root.left) + 1;
        int right = maxDepth(root.right) + 1;
        return Math.max(left, right);
    }
}

回溯

子集问题

在这里插入图片描述

class Solution {

    List<List<Integer>> ans = new ArrayList<>();
    List<Integer> path = new ArrayList<>();

    public List<List<Integer>> subsets(int[] nums) {
        dfs(0, nums);
        return ans;
    }

    public void dfs(int idx, int[] nums){
        if(idx == nums.length){
            ans.add(new ArrayList<>(path));
            return;
        }
        path.add(nums[idx]);
        dfs(idx + 1, nums);
        path.remove(path.size() - 1);
        dfs(idx + 1, nums);
    }
}

全排列问题

在这里插入图片描述

class Solution {
    public List<List<Integer>> permute(int[] nums) {
        List<List<Integer>> ans = new ArrayList<>();
        List<Integer> path = new ArrayList<>();
        boolean[] visited = new boolean[nums.length];
        dfs(ans, path, visited, nums);
        return ans;
    }
    public void dfs(List<List<Integer>> ans, List<Integer> path, boolean[] visited, int[] nums){
        if(path.size() == nums.length){
            ans.add(new ArrayList<>(path));
            return;
        }
        for(int i = 0; i < nums.length; i++){
            if(!visited[i]){
                visited[i] = true;
                path.add(nums[i]);
                dfs(ans, path, visited, nums);
                visited[i] = false;
                path.remove(path.size() - 1);
            }
        }
    }
}