初等数论

初等数论

大佬们一个晚上讲完了n个知识点，蒟蒻只能事后默默的记下来了……
一点点关于超级初等的数论的听课笔记，可能会有不充足或者顺序不对的地方，请见谅（毕竟我是蒟蒻嘛）……

前言

１、求出所有因子

//求x的所有因子
for (int i = 1; i * i <= x; ++i)
  if (x % i == 0) {
    ans[++cnt] = i;
    if (i * i != x) ans[++cnt] = x / i;
  }

２、线性筛素数

//筛素数
inline void solve(int n) {
  check[0] = 1, check[1] = 1;
  for (int i = 2; i <= n; ++i) {
    if (!check[i]) prim[++tot] = i;
    for (int j = 1; j <= tot && i * prim[j] <= n; ++j) {
      check[i * prim[j]] = 1;
      if (i % prim[j] == 0) break;
    }
  }
}

题目链接hihocoder 1295

欧几里德

１、欧几里得算法（辗转相除法）

如果要求两个数a、b的最小大公约数，可以采取欧几里得算法：

inline int gcd(int x, int y) {
  return (x % y == 0) ? y : gcd(y, x % y);
}

２、扩展欧几里得算法（解不定方程ax + by = c）

如果要找到不定方程ax + by = gcd(a, b)（a, b为常数）的任意一组解(x1, y1)可以使用扩展欧几里得算法：

inline void exgcd(int a, int b, int& d, int& x, int& y) {//d = gcd(a, b)
  if (!b) d = a, x = 1, y = 0;
  else {
    exgcd(b, a % b, d, y, x);
    y -= x * (a / b);
  }
}

证明如下：

设：ax1 + by1 = gcd(a, b)，bx2 + (a % b)y2 = gcd(b, a % b)

显然由欧几里得的性质可知gcd(a, b) = gcd(b, a % b)，所以ax1 + by1 = bx2 + (a % b)y2

所以有：ax1 + by1 = bx2 + (a - a / b * b) y2 = ay2 + b(x2 - (a / b)y2)

所以：x1 = y2, y1 = x2 - (a / b)y2；

题目链接hihocoder 1297

３、乘法逆元

如果a * b≡1(mod m)(这是同余方程，后文会有介绍)且(a, m) = 1，那么就说b是a模m时的乘法逆元

在运算中除以一个数取模等于乘以这个数的逆元后再取模

乘法逆元一般可以直接用扩展欧几里得求，即不定方程ab - km = gcd(a, m)的解(b1, k1)中的b1

也可以用后文提到的费马小定理求m是质数时的逆元：因为a^(m - 1)≡1(mod m)，所以a * a ^ (m - 2) ≡1(mod m)，b = a ^ (m - 2)（用快速幂求即可）

还有一种线性求逆元的方法：A[i]=-(p/i)*A[p%i];

同余和剩余

１、同余方程：a≡b(mod m)

如果m是a - b的一个因子，那么就说a，b关于模m同余，即为a≡b(mod m)

如果有a≡b(mod m)，那么b就是a模m的一个剩余

有关性质:传递性、同加减乘，不同除

２、线性同余方程

对于线性同余方程ax≡b mod n来说，可以将其转化为一个线性不定方程，即：ax - ny = b

贝祖定理：设两个正整数a、b的最大公约数gcd(a, b)=k，则关于两未知数x、y的方程（贝祖等式）ax+by=m当且仅当m是k的倍数时存在整数解，而当贝祖等式有解时，必然有无穷多个整数解。

由于贝祖定理可知：当gcd(a, n)不是b的约数时，方程无解，否则方程两边同时除以gcd后用扩展欧几里得及乘法逆元解决

当我们用扩展欧几里得算法求出一对解(x0, y0)后，因为如果ax0 + by0 = c成立，那么所有的x = x0 + bt, y = y0 - at均成立，所以如果我们求出同余方程的一个解后，可以直接不停的加上n / d

３、中国剩余定理

该方程组的通解为：

其中，，为模的逆元。

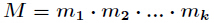
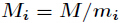
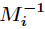
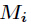
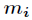
inline void exgcd(int a, LL b, LL& xx, LL& yy){
  if (!b) {xx = 1, yy = 0;}
  else {
    exgcd(b, a % b, yy, xx);
    yy -= (a / b) * xx;
  }
}

inline LL CRT(int n, int a[], int m[]) {
  LL M = 1, x = 0, xx, yy;
  for (int i = 1; i <= n; ++i) M *= m[i];
  for (int i = 1; i <= n; ++i) {
    LL w = M / m[i];
    exgcd(m[i], w, xx, yy);
    x = (x + yy * w * a[i]) % M;
  }
  return (x + M) % M;
}

题目链接hihocoder 1303（这道题不能用通解去求）

欧拉函数及欧拉定理

１、剩余类

模m的一个剩余类是由与某个给定的剩余(mod m)同余的所有数组成的一个类，总共m个剩余类，可分别由0, 1, 2, 3, …,m - 1代表，如m = 5时：

0：0, 5, 10,…

1：1, 6, 11,…

2：2, 7, 12,…

……

２、完全剩余系

任何m个分别属于这m个剩余类的数组成的一个集合，都称为模m的一个完全剩余系（完系）

３、缩剩余系（φ(m)）

我们用φ(m)表示不大于m的正整数中与m互质的正整数的个数，φ(m)也是m的欧拉函数值

显然对于质数p有：φ(p)＝p - 1，如φ(５)＝4(1, 2, 3, 4)

对与非质数p有：，以下是自己的证明

(1)证明φ(p)是积性函数：如果f(a) * f(b) = f(a * b)，其中(a, b)＝1，那么f(x)是积性函数
对于φ(mn)可以有如下矩阵：
1   m + 1   2m + 1   …   (n - 1)m + 1

2   m + 2   2m + 2   …   (n - 1)m + 2

………………………………………...

m   2m         3m      …   nm

图１

对于第r（0 < r < m）行第k号元素(k - 1)m + r，显然有(k - 1)m与mn不互质，那么如果r与m不互质且n与m互质，那么整行都与mn不互质（证明不言而喻），对于第m行，显然整行都与mn不互质，所以每一列中与mn互质的个数是φ(m)

而如果将mn互换，即将矩阵变形（旋转90度）为图2：

1   n + 1   2n + 1   …   (m - 1)n + 1

2   n + 2   2n + 2   …   (m - 1)n + 2

………………………………………...

n      2n       3n      …   mn

图２

显然仍有每一列中与mn互质的个数为φ(n)，而相对于图1，就是每一行中与mn互质的个数是φ(n)

综上：φ(mn) = φ(m) * φ(n)，所以φ(m)具有积性

(2)对于某个数k，设k = p^c，则所有比k小φ(m)的正整数中与k不互质的个数为p^(c - 1) - 1个：

p * 1, p * 2, p * 3,…,p * p ^ (c - 1) - 1)

又因为一共有p^c - 1个数比k小，所以φ(p) = p ^ c - p ^ (c - 1) = p ^ c * (1 - 1 / p)
(3)结合(1)、(2)点可推出

所以有代码：

//计算某个数m的phi值
  while (cin >> n && n != 0) {
    LL ans = n;
    if (n % 2 == 0) {while (n % 2 == 0) n /= 2; ans = ans / 2;}
    for (LL i = 3; i * i <= n; i += 2) {
      if (n % i == 0) {
        ans = ans / i * (i - 1);
        while (n % i == 0) n /= i;
      }
    }
    if (n > 1) ans = ans / n * (n - 1);
    cout << ans << endl;
  }
  return 0;

//计算1~n的phi值
phi[1] = 1;
  for (int i = 2; i <= n; ++i)
    if (!phi[i])
      for (int j = i; j <= n; j += i) {
    if (!phi[j]) phi[j] = j;
    phi[j] = phi[j] / i * (i - 1);
      }

关于欧拉函数还有一些神奇的性质：

(1)n为一个正整数：

∑d|nφ(d)=n

(2)1 <= k <= n：

∑(k, n) = 1k=nφ(n)/2

题目链接hihocoder 1298

４、费马小定理

费马小定理其实是欧拉定理的一种特殊情况：

当p是一个质数，且a、p互质时：

证明如下：

设p的完全剩余系为：P=｛1, 2, 3, 4, …,p - 1｝；

因为(a, p) = 1，所以A = ｛a, 2a, 3a, …,(p - 1)a｝也是p的完全剩余系；

又完全剩余系的定义：a * 2a * 3a *…*(p - 1)a % p = 1 * 2 * 3 * … *(p - 1)；

所以有(p - 1)!≡a^(p - 1) * (p- 1)!(mod p)；

显然有((p - 1)!, p) = 1，所以a^(p - 1)≡1(mod p)；

５、欧拉定理

当a、n互质时，有

证明可以类似的参考上面用φ(n)的性质去证明(其实当n为质数时，φ(n) = n - 1，即为费马小定理)，在此就不赘述了

原根与离散对数

-->ACM以后补充

１、CJOJ 1508

２、原根和离散对数-->蓝书126