数论学习&总结（只能说是初级）

最新推荐文章于 2022-02-08 23:41:20 发布

I_have_a_world

最新推荐文章于 2022-02-08 23:41:20 发布

阅读量583

点赞数

分类专栏： # ACM_模板大全 # ACM_数论文章标签：数论模板

本文链接：https://blog.csdn.net/I_have_a_world/article/details/116750972

版权

ACM_模板大全同时被 2 个专栏收录

37 篇文章 1 订阅

订阅专栏

ACM_数论

31 篇文章 0 订阅

订阅专栏

写在前面

参考博客

一、《算法竞赛中的初等数论》（一）正文 0x00整除、0x10 整除相关（ACM / OI / MO）（十五万字符数论书）

二、一些好玩的数学题

三、emmm还是先直接上题单罢：“kuangbin带你飞”专题计划——专题十四：数论基础

推荐拓展学习：夜深人静写算法（三）- 初等数论入门

写在前面

1.了解了一会，发现数论的知识太多了，仅一个多项式就要人命。还是像网络流一样，先初级罢，后面再和队友分任务。

参考博客

1.专题传送门：[kuangbin带你飞]专题1-23

2.不知道这个专题涉及了多少知识，主要是想找个机会好好学习一下各种知识。

多阅读些东西，决定学些什么东西：【已更新】《算法竞赛中的初等数论》（ACM / OI / MO）前言、后记、目录索引（十五万字符的数论书）、oi-wiki数学部分

ps：竟不知道繁凡さん大佬数论也学了那么多知识了，蓝桥杯差了点可能只是某些知识有点欠缺。tql，只能争取我的学习效率能不断增强。

有的人仰望就够了，他的成就与你无关。我想从他那里得到的，不过是勇气和动力罢了。

3.学哪些知识？神O的数论全家桶

4.逼乎推荐的题单：一些好玩的数学题（洛谷可能写起来轻松很多，主要是少了很多读题的麻烦。至于所需的读题能力，有时刷刷poj罢）、

一、《算法竞赛中的初等数论》（一）正文 0x00整除、0x10 整除相关（ACM / OI / MO）（十五万字符数论书）

二、一些好玩的数学题

三、emmm还是先直接上题单罢：“kuangbin带你飞”专题计划——专题十四：数论基础

素数筛

埃氏筛

int p[N], vis[N];
void Prime(int n) {
    int i, j;  //快一点点
    for (i = 2; i <= n; i++) {
        if (vis[i]) continue;
        p[++p[0]] = i;
        for (j = 2 * i; j <= n; j += i) vis[j] = 1;
    }
}

欧拉筛（线性筛）

int p[N], vis[N];
void Prime(int n) {
    int i, j;
    for (i = 2; i <= n; i++) {
        if (!vis[i]) p[++p[0]] = i;
        //注意，进入循环的并非都是素数
        for (j = 1; j <= p[0]; j++) {
            if (i * p[j] > n) break;
            vis[i * p[j]] = 1;
            if (i % p[j] == 0) break;
            //防止重复。比如4*2=8,4*3=12，12还是留在6*2的时候筛
        }
    }
}

欧拉函数

欧拉函数的定义

互质：可以理解为最大公因数为1。

所以，小于等于1和1互质的数只有1
小于等于2和2互质的数只有1
小于等于10和10互质的数有1，3，7，9

欧拉函数只是一个定义

欧拉函数的一些性质

1.欧拉函数是积性函数

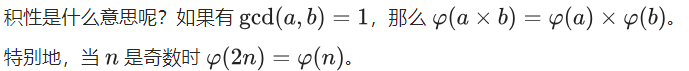
所以： $\varphi (180)=\varphi(2^2)*\varphi(5)*\varphi(3^2)$

2.

即 $18=\varphi(1)+\varphi(2)+\varphi(3)+\varphi(6)+\varphi(9)+\varphi(18)$

3.

即 $\varphi(3^5)=(3-1)*3^4$ 。根据定义，3^5个数中，每3个就有3-1个数与3^5互质（1,2,x,4,5,x,6,7,x,8.......）

4.

证明：

用到了第一条性质
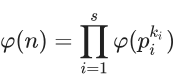
用到了第三条性质

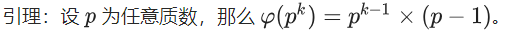
模板

//由性质四求某个数的欧拉函数
int euler_phi(int n) {
    int ans = n;
    for (int i = 2; i * i <= n; i++)
        if (n % i == 0) {
            ans = ans / i * (i - 1);
            while (n % i == 0) n /= i;
        }
    if (n > 1) ans = ans / n * (n - 1);
    return ans;
}

//由性质四，线性筛求欧拉函数。时间复杂度和埃氏筛一样
void phi_table(int n, int* phi) {
    for (int i = 2; i <= n; i++) phi[i] = 0;
    phi[1] = 1;
    for (int i = 2; i <= n; i++) {
        //素数才进行操作
        if (!phi[i]) {
            for (int j = i; j <= n; j += i) {
                if (!phi[j]) phi[j] = j;  //还没操作的时候另phi[j]=j
                phi[j] = phi[j] / i * (i - 1);  //会遇到j的每一个素数
            }
        }
    }
}

ps：欧拉定理以及拓展欧拉定理，并没有理解（没去理解）。

欧拉定理

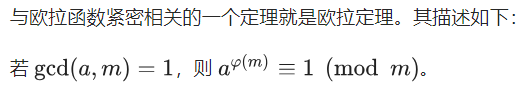
扩展欧拉定理

例题

1.Bi-shoe and Phi-shoe LightOJ - 1370 (线性筛+欧拉函数)

唯一分解定理

参考博客：唯一分解定理一篇就够了

唯一分解定理

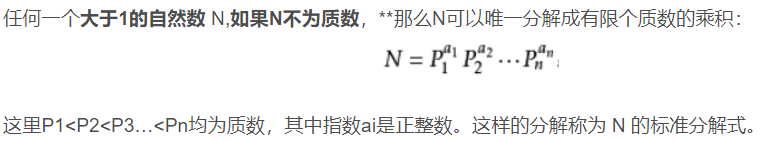
定理应用

所有因数的个数：Aladdin and the Flying Carpet LightOJ - 1341 （唯一分解定理+线筛+一个数的因数个数）
所有因数的和：Sigma Function LightOJ - 1336 （Sigma函数+一个数的所有因子和）
求lcm，gcd：Pairs Forming LCM LightOJ - 1236 （唯一分解定理的应用+线筛+MLE的情况）
求组合数？？（这里不是好懂）

之前竟然没注意到这个性质这里已经总结了emm。前n项和公式代入即可。

数论基本定理，还是很重要的
前两个应用是我之前不知道的，第3，4个应用好像没啥乱用emm

欧拉常数

调和级数公式：（n越大，误差越小，其中欧拉常数C=0.57721566490153286060651209）。具体见：Harmonic Number LightOJ - 1234 （调和级数+欧拉常数+打表）

情形说明：

1.求一个整数N，满足如以下的条件：

2.除数为bi，余数为ai。

3.显然ai<bi。

4.数组b中任意两个数应该互质（好像可以不互质，但是这里只学了互质的情形）

算法操作：

1.求所有bi的乘积lcm，即求 $lcm=\prod bi$

2.求Mi，其中 $Mi=lcm/bi$

3.求1/Mi，即Mi的逆元（注意是在bi意义下的逆元）。（因为任意两个bi，bj互质，所以 $gcd(lcm/bi,bi)=1$ 一定成立）。

4.求ci，其中 $ci=Mi*inv(Mi)$

5.答案 $ans=\prod (ai*ci)%lcm$

模板

例题：P3868 [TJOI2009]猜数字

拓展欧几里得求逆元：逆元3种方法简述

#include <bits/stdc++.h>
#define int long long
#define read(x) scanf("%lld", &x)
#define print(a, c) printf("%lld%c", a, c)
#define dbg(x) cout << #x << "===" << x << endl
using namespace std;
const int N = 20;

int n, a[N], b[N];

int exgcd(int a, int b, int &x, int &y) {
    if (a == 0 && b == 0) return -1;  //好像没啥卵用
    if (b == 0) {
        x = 1, y = 0;
        return a;
    }
    int g = exgcd(b, a % b, y, x);
    y -= a / b * x;
    return g;
}
//因为任意两个b[i]互质，所以lcm/b[i]在b[i]意义下的逆元一定存在，因为gcd(lcm/b[i],b[i])=1
int inv(int a, int M) {
    int X0, Y0;
    int g = exgcd(a, M, X0, Y0);
    return (g == 1) ? (X0 % M + M) % M : -1;  //-1不存在逆元
}
//龟速乘，以下所有值不会超过2*lcm，保证了不会超long long
int qmul(int a, int b, int mod) {
    int res = 0;  //注意这里也变成了0
    while (b) {
        if (b & 1) res = (res + a) % mod;
        b >>= 1, a = 2 * a % mod;
    }
    return res;
}
int china() {
    int ans = 0, lcm = 1;
    int M, c;
    for (int i = 1; i <= n; i++) lcm *= b[i];
    for (int i = 1; i <= n; i++) {
        M = lcm / b[i];
        c = M * inv(M, b[i]) % lcm;  // inv(M)是对bi取余，a[i]*c[i]都是对lcm取余
        // ans = (ans + c * a[i] % lcm) % lcm;
        //以上操作。最大可能出现的数达到lcm^2数量级会爆long long，需要使用快速乘
        // inv中的数不会超过max(bi)
        ans = (ans + qmul(c, a[i], lcm)) % lcm;
        // qmul中c在前会快一点，因为一半ai<bi小一点
    }
    return (ans + lcm) % lcm;
}
signed main() {
    read(n);
    int lcm = 1;
    for (int i = 1; i <= n; i++) read(a[i]);
    for (int i = 1; i <= n; i++) read(b[i]);
    for (int i = 1; i <= n; i++) a[i] = (a[i] % b[i] + b[i]) % b[i];
    //这是为何。使符合中国剩余定理的条件ai=N%bi，则ai<bi
    // bi|(N-ai)，看来意思是(N-ai)是bi的整数倍，不管这个整数是多少（<=0也oK）
    print(china(), '\n');
    return 0;
}

解决模指数方程

基础篇：,a,p互质

进阶篇：

扩展篇：

BSGS算法模板及简单讲解

基础篇：,a,p互质

（其实只争对这个题em）：Emoogle Grid UVA - 11916 （BSGS算法，a^x+by=c求x）

求最小的非负数x满足 $a^x \equiv b(mod\ p)$

1.参考资料：io-wiki-BSGS、BSGS

2.简单来说，只需要理解以下几个点：

a^x%p是一个周期数，因为a^x%p即相当于a^(x-1)%p^a%mod。不多说，自己可以手推一下。
手推1%7=1,1*3%7=3,3*3%7=2,2*3%7=6,6*3%7=4,4*3%7=5,5*3%7=1,1*3%7=1,,,,,,惊奇的发现周期为phi[p]。结论（不是由以上证明，以上只是引出）：x不超过phi[p]
将这phi[p]个数分布在一个面积大于p的正方形格子中，即x=i*m+j，则 $a^x \equiv b(mod\ p)$ => $a^{m^i}\equiv b/a^j(mod\ p)$ 。先枚举j求b/a^j的模数，再枚举i求(a^m)^i的模数，如果有某个j满足条件则i*m+j为解。
tql

模板：

//求满足a^x+p*y=b的最小非负数x。返回-1表示没有答案
int BSGS(int a, int b, int p) {
    //答案x=i*m+j.分成一块正方形，复杂度最高sqrt(p)*log(p)就可以解出x，如果解不出，只能说无解（具有周期性，且余数个数不会超过phi[p]）
    int m = (int)ceil(sqrt(1.0 * p));
    map<int, int> mp;
    int t = b, i, j, inv_a = qpow(a, p - 2, p),
        a_m = qpow(a, m, p);  // a_i表示的是a^m
    mp[b] = 0;                //每一行0~m-1
    for (j = 1; j < m; j++) {
        t = t * inv_a % p;
        if (!mp[t]) mp[t] = j;  //模数相等，只需要最小的i
    }
    t = 1;
    for (i = 0; i < m; i++) {
        if (mp[t]) return i * m + mp[t];
        t = t * a_m % p;
    }
    return -1;  //无解
}

推荐拓展学习：夜深人静写算法（三）- 初等数论入门

I_have_a_world

关注

0
点赞
踩
2

收藏

觉得还不错? 一键收藏
0
评论
数论学习&总结（只能说是初级）

1.专题传送门：[kuangbin带你飞]专题1-23 2.不知道这个专题涉及了多少知识，主要是想找个机会好好学习一下各种知识。多阅读些东西，决定学些什么东西：【已更新】《算法竞赛中的初等数论》（ACM / OI / MO）前言、后记、目录索引（十五万字符的数论书）、oi-wiki数学部分ps：竟不知道繁凡さん大佬数论也学了那么多知识了，蓝桥杯差了点可能只是某些知识有点欠缺。tql，只能争取我的学习效率能不断增强。有的人仰望就够了，他的成就与你无关。我想从他那里得到的，不过是勇气和动力罢了.
复制链接

扫一扫