“回文子串、最长回文子序列”总结，动态规划再显神通（Java实现）

陈亦康

已于 2023-04-22 20:13:29 修改

阅读量1.8k

点赞数 6

分类专栏：算法文章标签： java 算法动态规划 leetcode

于 2023-01-29 07:00:00 首次发布

本文链接：https://blog.csdn.net/CYK_byte/article/details/128776014

版权

算法专栏收录该内容

15 篇文章 0 订阅

订阅专栏

一、回文子串

题目描述：

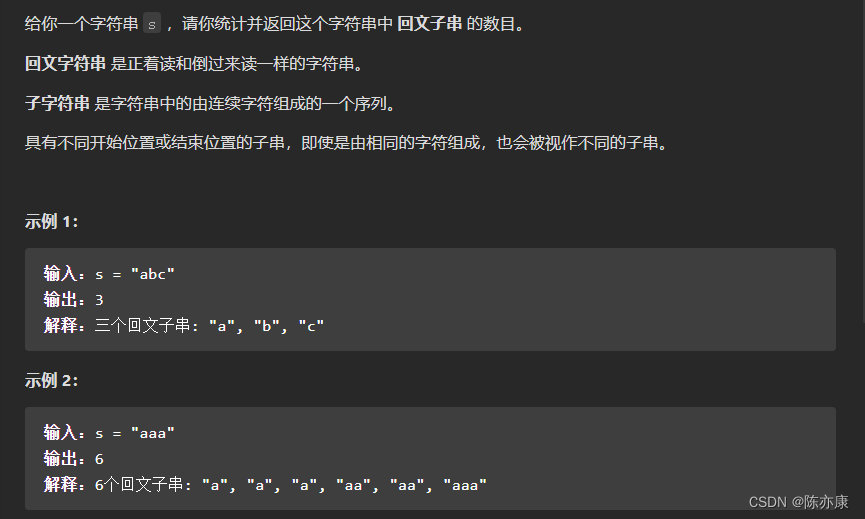
题目来源：647. 回文子串

1.1、dp定义

分析：

如果这里我们继续像以往那样定义成“以字符串第i个元素为结尾...”，如果尝试过，你就会发现很难找出dp[i]这个状态的推导，看到回文子串，因该更多的去想到他的回文特性，因此，可以定义一个二维的dp数组，来表示字符串的区间[i, j]是否回文。

dp定义：

dp[i][j]（布尔类型）：区间[i, j]是否为回文子串。

1.2、递推公式

分析：

根据回文串的性质，我们可以这样想，如果一个字符串的左右两端的字符相同，并且除了这两个字符的中间的字符串是回文串，那么他整体就是一个回文串，如下图：

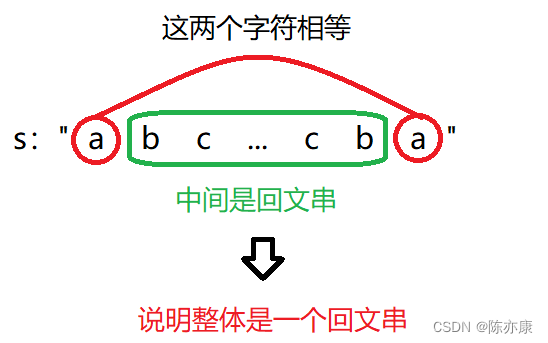
并且当[i, j]这个区间长度小于等于1时，是一定回文的！

状态转移方程：

if(s.charAt(i) == s.charAt(j)) { //左右两端字符相等
    if(j - i <= 1) { //区间长度小于等于1
       dp[i][j] = true;
       result++;
    } else if(dp[i + 1][j - 1]) { //中间是回文串
        dp[i][j] = true;
        result--;
    }
}

注意：dp只是用来判断当前区间的字符串是否为回文串，一旦判断是回文串，需要用一个计数器来记录。

1.3、初始化

分析：

由递推公式可以看出，我们让dp的每一个值都先为false ，通过递推才能知道哪些值为true；

1.4、遍历顺序

从递推公式中可以看出会用到的状态只有dp[i + 1][j - 1]，如下图：

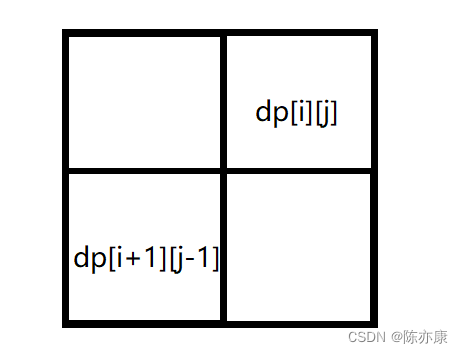
也就是说需要从左下角才能推出dp[i][j]，那么我们就需要从下往上，从左往右遍历~

1.5、解题代码

class Solution {
    public int countSubstrings(String s) {
        int len = s.length();
        boolean[][] dp = new boolean[len][len];
        int result = 0;
        for(int i = len - 1; i >= 0; i--) {
            for(int j = i; j < len; j++) {
                if(s.charAt(i) == s.charAt(j)) {
                    if(j - i <= 1) {
                       dp[i][j] = true;
                       result++;
                    } else if(dp[i + 1][j - 1]) {
                        dp[i][j] = true;
                        result++;
                    }
                }
            }
        }
        return result;
    }
}

二、最长回文子序列

题目描述：

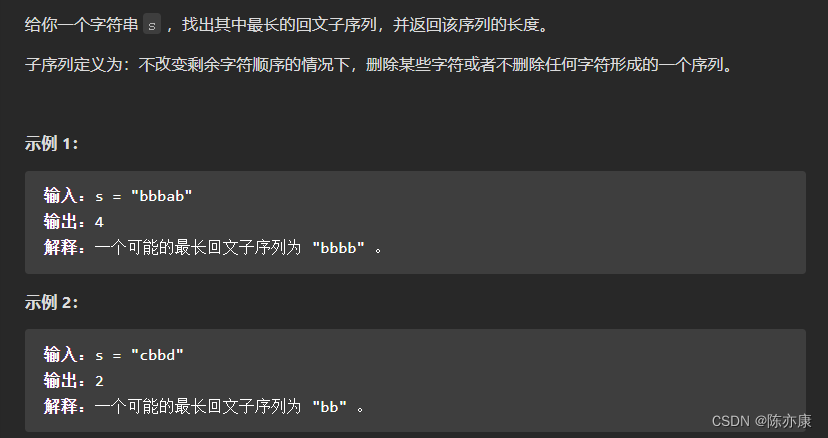
题目来源：516. 最长回文子序列

2.1、dp定义

分析：

由上一道题“回文子串”分析到，对于回文串的定义，想要利用上回文串的特点，就需要定义[i, j]这样一个区间，dp[i, j]就是最长回文子序列的长度。

dp定义：

dp[i][j]：在区间[i, j]里，最长回文子序列的长度。

2.2、递推公式

分析：

由上一道题“回文子串”分析到，如果一个字符串的左右两端的字符相同，并且除了这两个字符的中间的字符串是回文串，那么他整体就是一个回文串，（不理解的可以看看上一道题的递推公式分析）那么想要得到dp[i][j]，就有以下两种情况：

1.s[i] == s[j]，当两端的字符相等时，那么就可以由除了两端之外的中间的字符串的最长子序列长度dp[i + 1][j - 1] +2得到，这里的+2就表示加上两端字符的长度，如下图：

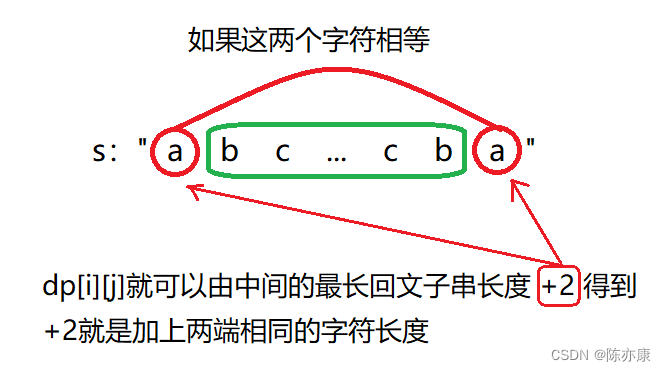
2.s[i] != s[j]，当两端的字符不相等时，那么要考虑忽略s[i]或者s[j]然后挑选出回文子序列长度最长的字符串，如下图：

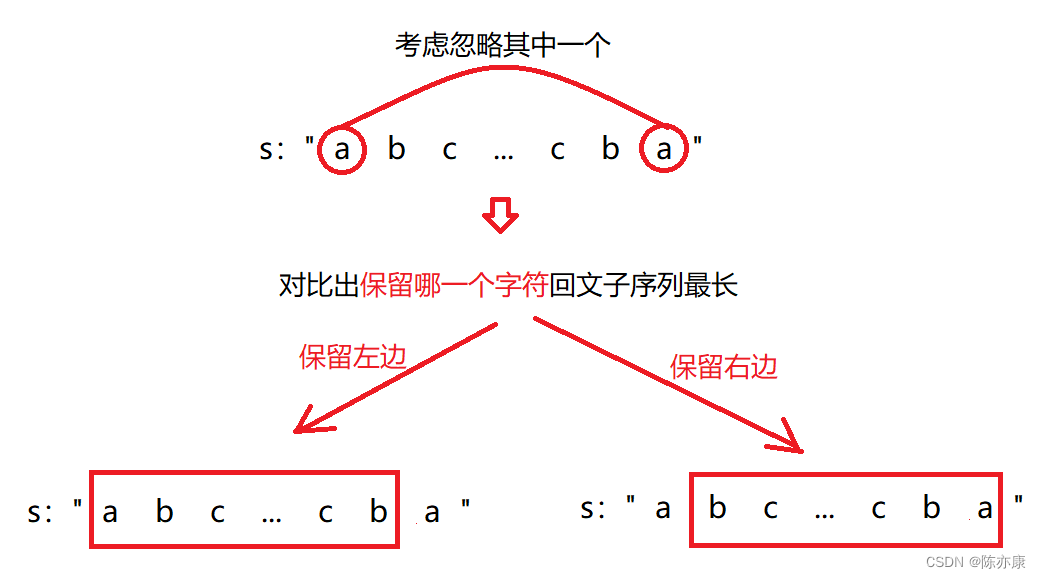
动态转移方程：

if(s.charAt(i) == s.charAt(j)) {
    dp[i][j] = dp[i + 1][j - 1] + 2;//两端的元素都考虑
} else {
    dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);//两端元素只考虑最大的
}

2.3、初始化

分析：

由递推公式可以看出，需要的状态有：dp[i + 1][j - 1]、dp[i + 1][j]、 dp[i][j - 1]，将这些状态一直推下去，就可以找到源头就是dp[i][j]（这里i == j），i等于j，就意味区间为[i, j]指向的是同一个字符，那么必然是回文的，所以初始化为1。

初始化：

dp[i][i] = 1；（这里i, i表示i等于j）

2.4、遍历顺序

分析：

由递推公式可以看出，由下图中的几个方向可以推导出dp[i][j]：

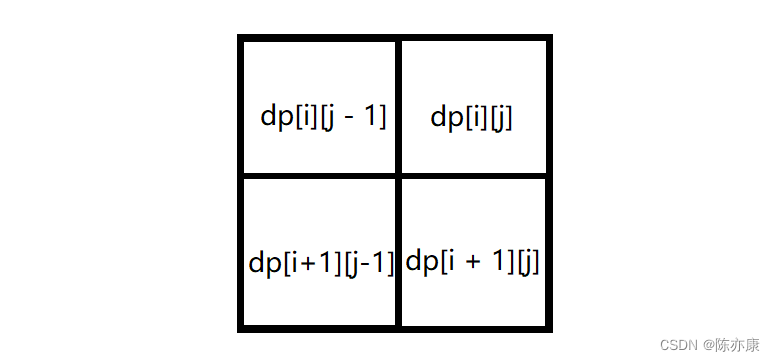
那么我们就需要从下往上，从左往右遍历~

2.5、解题代码

class Solution {
    public int longestPalindromeSubseq(String s) {
        int len = s.length();
        int[][] dp = new int[len][len];
        //初始化
        for(int i = 0; i < len; i++) {
            dp[i][i] = 1;
        }
        //递推
        for(int i = len - 1; i >= 0; i--) {
            for(int j = i + 1; j < len; j++) {
                if(s.charAt(i) == s.charAt(j)) {
                    dp[i][j] = dp[i + 1][j - 1] + 2;//两端的元素都考虑
                } else {
                    dp[i][j] = Math.max(dp[i + 1][j], dp[i][j - 1]);//两端元素只考虑最大的
                }
            }
        }
        return dp[0][len - 1];
    }
}