动态规划之最长回文子串

问题：给出一个字符串S，求S的最长回文子串的长度。

结果：字符串"PATZJUJZTACCBCC"的最长回文子串为"ATZJUJZTA",长度为9。

暴力解法

枚举子串的两个端点i和j,判断在[i, j]区间内的子串是否回文。从复杂度上来看，枚举端点需要0(n2),判断回文需要0(n)，因此总复杂度是O(n3)。
        
动态规划解决
        令dp[i][j]表示S[i]至S[j]所表示的子串是否是回文子串，是则为1，不是为0。这样根据S[i]是否等于S[j]，可以把转移情况分为两类：
         ①若S[i]=S[j],那么只要S[i+1]和S[j-1]是回文子串，S[i]至S[j]就是回文子串；如果S[i+1]至S[j-1]不是回文子串，则S[i]至S[j]一定不是回文子串。
         ②若S[i]!=S[j]，那S[i]至S[j]一定不是回文子串。
由此可以写出状态转移方程
 

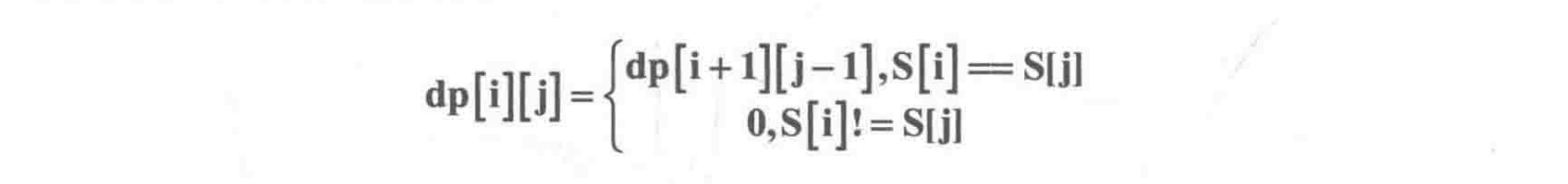
边界dp[i][i]=1,dp[i][i+1]=(S[i]==S[i+1])?1:0 。

到这里还有一个问题没有解决,那就是如果按照i和j从小到大的顺序来枚举子串的两个端点,然后更新dp[i]lj],会无法保证dp[i + 1][j - 1]已经被计算过,从而无法得到正确的dp[i][i]。
         如图11-4所示，先固定i=0,然后枚举j从2开始。当求解dp[0][2]时，将会转换为dp[1][1],而dp[1][1]是在初始化中得到的;当求解dp[0][3]时,将会转换为dp[1][2], 而dp[1][2]也是在初始化中得到的;当求解dp[0][4]时，将会转换为dp[1][3], 但是dp[1][3]并不是已经计算过的值，因此无法状态转移。事实上，无论对i和j的枚举顺序做何调整，都无法调和这个矛盾，因此必须想办法寻找新的枚举方式。
        根据递推写法从边界出发的原理，注意到边界表示的是长度为1和2的子串，且每次转移时都对子串的长度减了1,因此不妨考虑按子串的长度和子串的初始位置进行枚举，即第一遍将长度为3的子串的dp值全部求出，第二遍通过第一遍结果计算出长度为4的子串的dp值…这样就可以避免状态无法转移的问题。如图11-5所示，可以先枚举子串长度L (注意: L是可以取到整个字符串的长度S.len()的)，再枚举左端点i,这样右端点i+ L- 1也可以直接得到。

public class Solution {

  public static void main(String[] args) {
    maxSubMirrorString("PATZJUJZTACCBCC");
  }

  public static void maxSubMirrorString(String str) {
    char[] chars = str.toCharArray();
    int length = chars.length;
    int dp[][] = new int[length][length];
    int maxSubMirrorStrLength = 1;

    //初始化dp[i][i],dp[i][i+1]
    for (int i = 0; i < length; i++) {
      dp[i][i] = 1;
      if (i < length - 1) {
        if (chars[i] == chars[i + 1]) {
          dp[i][i + 1] = 1;
          maxSubMirrorStrLength = 2;
        }
      }
    }

    //状态转移方程
    for (int L = 3; L <= length; L++) {//枚举子串长度
      //枚举子串起始端点 起始端点加上子串长度(子串长度包括他本身，所以要-1）必须小于总长
      int j;//子串右端点
      for (int i = 0; (j = i + L - 1) < length; i++) {
        if (chars[i] == chars[j] && dp[i + 1][j - 1] == 1) {
          dp[i][j] = 1;
          maxSubMirrorStrLength = L;//更新最长回文子串长度;
        }
      }
    }

    System.out.println("最长回文子串长度：" + maxSubMirrorStrLength);
  }
}