1005 Necklace (hdu5727)
题目
SJX has 2*N magic gems. N of them have Yin energy inside while others have Yang energy. SJX wants to make a necklace with these magic gems for his beloved BHB. To avoid making the necklace too Yin or too Yang, he must place these magic gems Yin after Yang and Yang after Yin, which means two adjacent gems must have different kind of energy. But he finds that some gems with Yang energy will become somber adjacent with some of the Yin gems and impact the value of the neckless. After trying multiple times, he finds out M rules of the gems. He wants to have a most valuable neckless which means the somber gems must be as less as possible. So he wonders how many gems with Yang energy will become somber if he make the necklace in the best way.
输入
Multiple test cases.
For each test case, the first line contains two integers N(0≤N≤9),M(0≤M≤N∗N), descripted as above.
Then M lines followed, every line contains two integers X,Y, indicates that magic gem X with Yang energy will become somber adjacent with the magic gem Y with Yin energy.
输出
One line per case, an integer indicates that how many gem will become somber at least.
题意
给N个阴珠子N个阳珠子,串成一个环。有些珠子挨在一起阳珠子会暗淡,求最小的变暗的珠子的个数。
解法
题解给了剪枝搜索的解法,这个还可以用KM来解决。
因为珠子有不同的排列,无法直接建图,因此可以先将阴珠子的排列固定,这样再进行二分图带权匹配,对于每一个阴珠子的排列,都进行一次匹配,取结果最小值即可。
注意:N=0特判
代码
#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <iostream>
using namespace std;
namespace KMA {
const int N = 15;
const int INF = 0x3f3f3f3f;
int nx,ny;//两边的点数
int g[N][N];//二分图描述
int linker[N],lx[N],ly[N];//y中各点匹配状态,x,y中的点标号
int slack[N];
bool visx[N],visy[N];
bool DFS(int x)
{
visx[x] = true;
for(int y = 0; y < ny; y++)
{
if(visy[y])continue;
int tmp = lx[x] + ly[y] - g[x][y];
if(tmp == 0)
{
visy[y] = true;
if(linker[y] == -1 || DFS(linker[y]))
{
linker[y] = x;
return true;
}
}
else if(slack[y] > tmp)
slack[y] = tmp;
}
return false;
}
int KM()
{
memset(linker,-1,sizeof(linker));
memset(ly,0,sizeof(ly));
for(int i = 0;i < nx;i++)
{
lx[i] = -INF;
for(int j = 0;j < ny;j++)
if(g[i][j] > lx[i])
lx[i] = g[i][j];
}
for(int x = 0;x < nx;x++)
{
for(int i = 0;i < ny;i++)
slack[i] = INF;
while(true)
{
memset(visx,false,sizeof(visx));
memset(visy,false,sizeof(visy));
if(DFS(x))break;
int d = INF;
for(int i = 0;i < ny;i++)
if(!visy[i] && d > slack[i])
d = slack[i];
for(int i = 0;i < nx;i++)
if(visx[i])
lx[i] -= d;
for(int i = 0;i < ny;i++)
{
if(visy[i])ly[i] += d;
else slack[i] -= d;
}
}
}
/*
for(int i = 0; i < nx; i++) {
for(int j = 0; j < ny; j++) {
printf("g[%d][%d]=%d\n",i,j,g[i][j]);
}
}*/
int res = 0;
for(int i = 0;i < ny;i++){
//printf("linker[%d]=%d\n",i,linker[i]);
if(linker[i] != -1)
res += g[linker[i]][i];
}
//printf("res=%d\n",res);
return res;
}
}
int N, M;
int A[15][15];
int y[15];
int main() {
while(~scanf("%d %d",&N,&M)) {
if(!N) {
printf("0\n");
continue;
}
memset(A,0,sizeof(A));
while(M--) {
int a, b;
scanf("%d %d",&a,&b);
A[a-1][b-1] = -1;
}
for(int i = 0; i < N; i++) y[i] = i;
KMA::nx = KMA::ny = N;
int res = 0x7fffffff;
do {
memset(KMA::g, 0, sizeof(KMA::g));
for(int i = 0; i < N; i++) {
for(int j = 0; j < N; j++) {
KMA::g[i][y[j]] = A[i][y[j]] |A[i][j?y[j-1]:y[N-1]];
}
}
res = min(res, -KMA::KM());
} while(next_permutation(y+1,y+N));
printf("%d\n",res);
}
}
1007 Rigid Frameworks(hdu5729)
题目
Note that you can add at most one orientation of a diagonal edge in one single cell. In fact, there are 448 ways to make a 2 × 3 grid graph rigid. And now we want to know, how many different rigid m × n grid graph with diagonal edges in total? Dear contestant, could you please find it out?
输入
There are multiple test cases. For each test case, the first line contains two integer m and n (1≤m,n≤10) represented the size of the grid graph.
输出
For each test case, output one integer number in a single line — the number of different rigid m × n grid graph with diagonal edges. The answer could be very large, output it modulo 1000000007(109+7).
题意
给你一个M*N的网格,对于每一个正方形网格,最多可以放一个对角线,问有多少种方案让这个网格固定。
解法
对于一个网格里面有没有对角线的状态,可以归约到一个二分图上。二分图左边M个顶点,右边N个。(若坐标(2,3)的网格有对角线,则第二个点和第三个点有一个边)。最终我们要找的就是连通二分图的个数。
连通二分图计数
B[i][j][k] 代表:左边有i个点右边有j个点有k的边的二分图有多少个不同的连通二分图。
B[i][j][k] = C(i*j,k) - sum{不符合条件的二分图的个数(即不是连通的)}
计算不符合条件的二分图的个数:
枚举二分图其中包含结点1的连通分支的大小(枚举左边点数ii和右边点数jj),枚举这个连通分支的边数kk,对于包含这个连通分支的二分图,个数为:
C(i-1,ii-1) * C(j,jj) * B[ii][jj][kk] * C((i-ii)*(j-jj), kk)
即
B[i][j][k] = C(i*j,k) - sum{ C(i-1,ii-1) * C(j,jj) * B[ii][jj][kk] * C((i-ii)*(j-jj), kk) }
代码
/*
author@ czw
*/
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int MOD = 1e9 + 7;
typedef long long ll;
ll power(ll a,ll b)
{
ll ans = 1;
a %= MOD;
while(b > 0)
{
if(b&1) ans = (ans*a)%MOD;
b >>= 1;
a = (a*a)%MOD;
}
return ans;
}
ll inv(ll n) {
return power(n, MOD - 2);
}
ll f[105];
ll C(ll n, ll m) {
if(n < m) return 0;
return f[n] * inv(f[m]) % MOD *inv(f[n-m]) %MOD;
}
ll B[15][15][105]; // B[i][j][k]表示 点数为i,j边数为k的连通二分图 种类数
ll b(int a, int b, int c){
if (a >= b) return B[a][b][c];
return B[b][a][c];
}
int main() {
f[0] = 1;
for(int i = 1; i <= 100; i++) f[i] = f[i - 1] * i % MOD; //阶乘
B[1][0][0] = 1;
for(int i = 1; i <= 10; i++) {
for(int j = 1; j <= i; j++) {
for(int k = 1; k <= i * j; k++) {
B[i][j][k] = C(i*j,k);
//先令B[i][j][k]等于所有种二分图的种类数,再减去不符合条件的
for(int ii = 1; ii <=i; ii++) {
//枚举二分图中左一排点中包含点1 的子集大小
for(int jj = 0; jj <= j; jj++) {
//枚举右一排子集大小
for(int kk = 0; kk <= min(k, ii * jj); kk++) {
//枚举 由ii *jj个点组成的二分子图的匹配数
if(b(ii, jj, kk) && (i-ii)*(j-jj) >= k-kk) {
if(i == ii && j == jj) break;
B[i][j][k] -= C(i-1, ii-1) * C(j, jj)%MOD * b(ii, jj, kk) %MOD* C((i-ii)*(j-jj), k-kk)%MOD;
while(B[i][j][k] < 0) B[i][j][k] += MOD;
//
}
}
}
}
}
}
}
int N, M;
while(~scanf("%d %d",&N,&M)) {
if(M > N) swap(N, M);
ll res = 0;
for(int i = 1; i <= N*M; i++) {
res = (res + B[N][M][i] * power(2, i)) % MOD;
//对于正方形对角线有两种摆放方式
}
printf("%I64d\n",res);
}
}
1006 PowMod(hdu5728)
题目
Declare:
k=∑mi=1φ(i∗n) mod 1000000007
n is a square-free number.
φ is the Euler’s totient function.
find:
ans=k^k^k^k^…^k mod p
There are infinite number of k
解法
官方题解写的还是比较清楚的
然后那个公式的推导在这:
这里用到了欧拉函数的一个性质:
设a为N的质因数,若(N % a == 0 && (N / a) % a == 0) 则有E(N)=E(N / a) * a;若(N % a == 0 && (N / a) % a != 0) 则有:E(N) = E(N / a) * (a - 1)。
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int mod = 1e9+7;
typedef long long ll;
namespace Eulr {
const int N=10000000;
bool check[N+5];
long long s[N+5];
int phi[N+5],tot,prime[N+5];
void getPhi(){
memset(check,false,sizeof(check));
phi[1]=1;
tot=0;
for(int i=2;i<=N;i++){
if(!check[i]){phi[i]=i-1;prime[tot++]=i;}
for(int j=0;j<tot;j++){
if(i*prime[j]>N)break;
check[i*prime[j]]=true;
if(i%prime[j]==0){
phi[i*prime[j]]=phi[i]*prime[j];break;
}else{
phi[i*prime[j]]=phi[i]*(prime[j]-1);
}
}
}
s[0]=0;
for(int i=1;i<=N;i++)s[i]=(s[i-1]+phi[i])%mod;
}
}
ll pow(ll a,ll b,int p){
ll now=1;
while(b!=0){
if(b%2==1)now*=a;
a*=a;b/=2;a%=p;
now%=p;
}
return now;
}
int solve(int n, int m) {
if(n == 1) return Eulr::s[m];
if(m == 1) return Eulr::phi[n];
if(m < 1) return 0;
for(int i=0;i<Eulr::tot;i++){
if(n%Eulr::prime[i]==0){
return (((ll)(Eulr::prime[i]-1)*solve(n/Eulr::prime[i],m)%mod+solve(n,m/Eulr::prime[i])%mod)%mod);
}
}
return 0;
}
ll cal(ll k,int p){
if(p==1)return 0;
ll now=cal(k,Eulr::phi[p]);
return(pow(k,now+Eulr::phi[p],p));
}
int main() {
Eulr::getPhi();
int n,m,p;
while(~scanf("%d %d %d",&n,&m,&p)) {
ll k = solve(n, m);
printf("%I64d\n",cal(k,p));
}
}











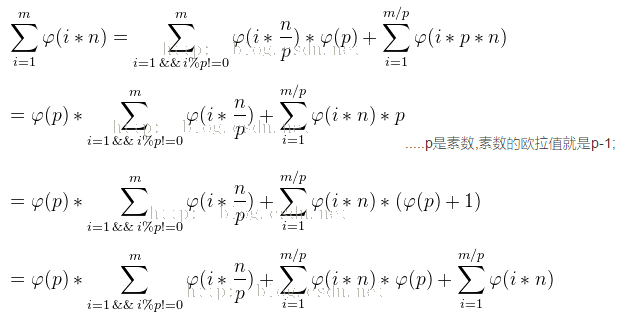














 402
402

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








