机器学习

监督学习

---

---

线性回归

线性回归主要是主要是根据数据集找到一条最接近的曲线，其实也即曲线拟合，线性回归采用的误差函数为最小二乘法：设

$$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+……=\sum_{i=0}^n\theta_ix_i,x_o=1$$
这只是直线，曲线方程应为 $$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2^2+……=\sum_{i=0}^n\theta_ix_i^i$$ $$J(\theta)=\frac1 2 \sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})^2$$ 然后让这个误差函数取得最小值即可。

---

梯度下降

LMS是采用梯度下降法来求得极小值：$\theta_j:=\theta_j-\alpha\frac \partial{\partial\theta_j}J(\theta)$，因为我们需要求出所有的$\theta$现在需要对$J(\theta)$求$\theta_j$的偏导，书上假设只有一组数据(x,y)：
$\frac\partial{\partial\theta_j}J(\theta)=\frac12\frac\partial{\partial\theta_j}(h_\theta(x)-y)^2$
$=2\cdot\frac12(h_\theta(x)-y)\cdot\frac\partial{\partial\theta_j}(h_\theta(x)-y)$
$=(h_\theta(x)-y)\cdot\frac\partial{\partial\theta_j}(\sum_{i=0}^n\theta_ix_i-y)$ ———–求和上面的n为主题数
$=(h_\theta(x)-y)x_j$………………j为求第j个参数时相应的那个主题下的数据
则对于只有一组数据的演化规则为：$\theta_j:=\theta_j+\alpha(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)}$ ———–$\alpha$为学习率
然后梯度下降需要做的是把数据集中的数据带入公式里面迭代得出最终的$\theta$

---

$n$ = 特征数目

$x^{(i)}$ = 第i组训练样本

$x_j^{(i)}$ = 第i组训练样本的第j个特征值

假设：$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_x$

For convenience of notation,define $x_0=1$ => $x_0^{(i)}=1$

$X=\left[\begin{matrix}x_0\\x_1\\x_2\\.\\.\\.\\x_n\end{matrix}\right]$，$\theta = \left[\begin{matrix}\theta_0\\\theta_1\\\theta_2\\.\\.\\.\\\theta_n\end{matrix}\right]$

SO we get that：$h_\theta(x)=\theta^\intercal X$

---

梯度下降法原理
梯度下降法主要是处理$J(\theta)$让$J(\theta)$得到最小值

---

接下来又分为两个梯度下降的算法：批量梯度下降（batch gradient descent）和随机梯度下降（stochastic gradient descent）

批量梯度下降

书上给的公式：
Repeat until convergence {
  $\theta_j:=\theta_j+\alpha\sum_{i=1}^m(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)}$   (for every j)
}

批量递归下降每一次循环都要遍历整个数据集，对于收敛性我们一般在计算机中不直接判断有没有收敛而是让他循环固定的次数或者当两次迭代的估价值小于某个数，调参数$\alpha$是关键。
接下来就是把数据带入求方程式组。
由公式可知每一步的$\theta$都要用到上一步所有$\theta$的值，所以要初始化一个theta数组

def matchGradientDescent(X,Y,alpha,numIterations):
    m = X.shape[0]
    n=X.shape[1]+1
    X = np.column_stack((np.ones(m), X))
    X=X.transpose()
    theta = np.zeros(n)
    for iter in range(0, numIterations):
        hypothesis = np.dot(theta,X)
        loss = hypothesis - Y
        for j in range(0,n):
            aJ=np.sum(loss*X[j])/m
            theta[j] = theta[j] - alpha * aJ
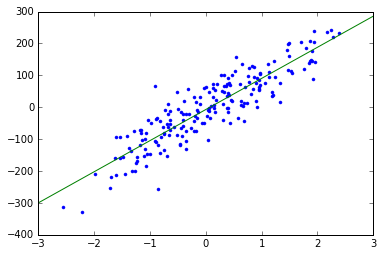
    return theta

下面是测试：

X,Y=make_regression(n_samples=200, n_features=1, n_informative=1, random_state=0, noise=50)
Y=np.array(Y).transpose()
theta=matchGradientDescent(X,Y,0.01,1000)
plt.plot(X,Y,'.')
x=np.arange(-3,3,0.01)
plt.plot(x,theta[0]+theta[1]*x)

---

随机梯度下降

随机梯度下降大哥给的证明：随机梯度下降
同样先给公式：
Loop {
  for i=1 to m , {
    $\theta_j:=\alpha(y^{(i)}-h_\theta(x^{(i)}))x_j^{(i)}$   (for every j)
  }
}

def stochasticGradientDescent(X,Y,alpha,numIterations):
    m = X.shape[0]
    n=X.shape[1]+1
    X = np.column_stack((np.ones(m), X))
    X=X.transpose()
    theta = np.zeros(n)
    for iter in range(0, numIterations):
        for i in range(0,m):
            for j in range(0, n):
                hypothesis = np.dot(theta, X[:,i])
                loss = hypothesis - Y[i]
                aJ = loss*X[j][i]
                theta[j] = theta[j] - alpha * aJ
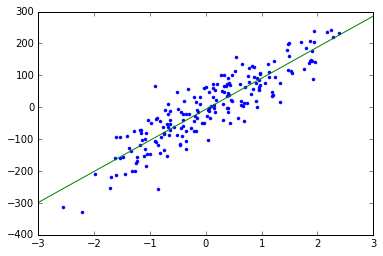
    return theta

测试：

x, y = make_regression(n_samples=200, n_features=1, n_informative=1, random_state=0, noise=50)
alpha = 0.01
y=np.array(y).transpose()
theta = stochasticGradientDescent( x, y,alpha, 1000) # plot
plt.plot(x, y, '.')
s = np.arange(-3, 3, 0.01)
plt.plot(s,theta[0]+theta[1]*s)

随机梯度下降在每一次进行迭代的时候用的只是其中的一组数据，但当m足够大时他会越来越接近最优解

---

有时候数据的模型不是直线相关的，我们也可以通过上面的方法进行曲线的拟合，原理类似泰勒公式：
假设函数：$h_\theta(x)=\theta_0+\theta_1x_1+\theta_2x_2+...+\theta_nx_n$
可以写成：$h_\theta(x)=\theta_0+\theta_1x^1+\theta_2x^2+...+\theta_nx^n$