虽然LTL和CTL的不同之处在之前都总结过了,不过这边再来单独对比一下,算是对之前知识的一个梳理。
LTL和CTL的等价
由之前的一张图我们看到,CTL和LTL有部分的表达是有交集的,这部分既可以用LTL表达,又可以用CTL表达,那么如何形式化地定义等价这个概念呢?

如果一个LTL公式
φ
φ
φ和一个CTL公式
Φ
\Phi
Φ是等价的(记为
φ
≡
Φ
φ\equiv\Phi
φ≡Φ),那么当且仅当,对于AP上的TS来说
T
S
⊨
φ
⇔
T
S
⊨
Φ
TS\vDash φ\Leftrightarrow TS\vDash\Phi
TS⊨φ⇔TS⊨Φ
例如有这些个公式是等价的
| CTL公式 Φ \Phi Φ | LTL公式 φ φ φ |
|---|---|
| a | a |
| ∀ ◯ a \forall\bigcirc a ∀◯a | ◯ a \bigcirc a ◯a |
| ∀ ( a U b ) \forall(aUb) ∀(aUb) | a U b aUb aUb |
| ∀ □ a \forall\Box a ∀□a | □ a \Box a □a |
| ∀ ◊ a \forall\Diamond a ∀◊a | ◊ a \Diamond a ◊a |
| ∀ ( a W b ) \forall(aWb) ∀(aWb) | a W b aWb aWb |
| ∀ □ ∀ ◊ a \forall\Box\forall\Diamond a ∀□∀◊a | □ ◊ a \Box\Diamond a □◊a |
LTL和CTL各自能表达的部分
由上面的文氏图我们知道,LTL和CTL的表达能力并不完全等价,因为存在着只要有各自能够表达的部分
某些LTL公式不能表示成CTL公式,例如
- ◊ □ a \Diamond\Box a ◊□a
- ◊ ( a ∧ ◯ a ) \Diamond(a\wedge\bigcirc a) ◊(a∧◯a)
某些CTL公式不能表示成LTL公式,例如
- ∀ ◊ ∀ □ a \forall\Diamond\forall\Box a ∀◊∀□a
- ∀ ◊ ( a ∧ ∀ ◯ a ) \forall\Diamond(a\wedge\forall\bigcirc a) ∀◊(a∧∀◯a)
- ∀ □ ∃ ◊ a \forall\Box\exist\Diamond a ∀□∃◊a
不等价案例
◊ ( a ∧ ◯ a ) \Diamond(a\wedge\bigcirc a) ◊(a∧◯a)与 ∀ ◊ ( a ∧ ∀ ◯ a ) \forall\Diamond(a\wedge\forall\bigcirc a) ∀◊(a∧∀◯a)不等价
例如下面这张图:

我们可以看到它能表示LTL公式
◊
(
a
∧
◯
a
)
\Diamond(a\wedge\bigcirc a)
◊(a∧◯a),但是不能表示CTL公式
∀
◊
(
a
∧
∀
◯
a
)
\forall\Diamond(a\wedge\forall\bigcirc a)
∀◊(a∧∀◯a),因为看到
S
0
,
S
3
S_{0},S_{3}
S0,S3这条路径,对于用CTL表示的
∀
◊
(
a
∧
∀
◯
a
)
\forall\Diamond(a\wedge\forall\bigcirc a)
∀◊(a∧∀◯a)来说,从
S
0
S_{0}
S0的角度看,它不满足所有的下一个状态a成立。
再看另一个例子, ◊ □ a \Diamond\Box a ◊□a和 ∀ ◊ ∀ □ a \forall\Diamond\forall\Box a ∀◊∀□a不等价
就如下图所示
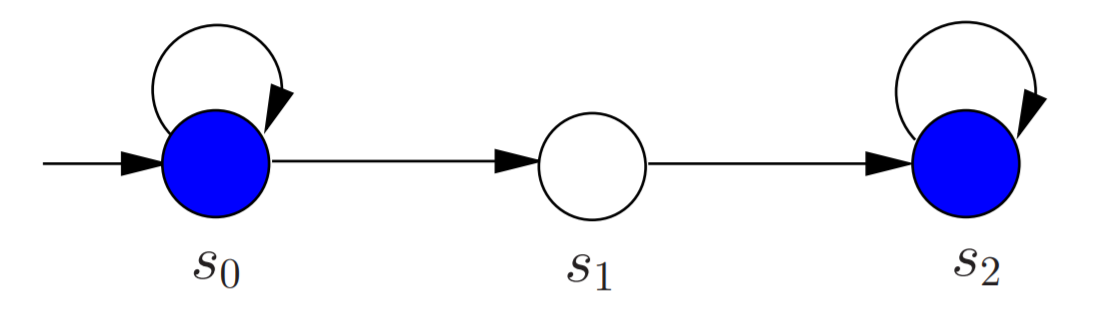
它能够表示LTL公式
◊
□
a
\Diamond\Box a
◊□a,但是不能表示CTL公式
∀
◊
∀
□
a
\forall\Diamond\forall\Box a
∀◊∀□a,我们把它的计算树画出来
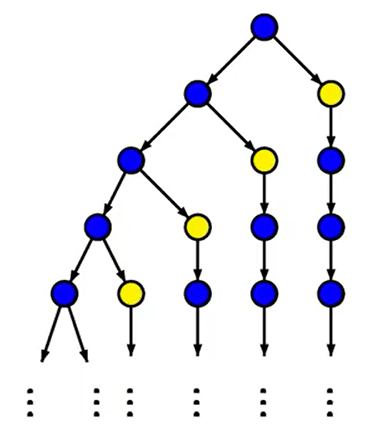
我们看到最左边的那条路径,也就是说如果走的路径为 S 0 S 0 S 0 S 0 S 0 S 0 . . . . S_{0}S_{0}S_{0}S_{0}S_{0}S_{0}.... S0S0S0S0S0S0....那么就会有一条路径不满足 ∀ ◊ ∀ □ a \forall\Diamond\forall\Box a ∀◊∀□a。
模型检测的复杂度
LTL模型检测的时间复杂度为
O
(
∣
T
S
∣
⋅
2
∣
ϕ
∣
)
O(|TS|·2^{|\phi|})
O(∣TS∣⋅2∣ϕ∣)
CTL模型检测的时间复杂度为
O
(
∣
T
S
∣
⋅
∣
ϕ
∣
)
O(|TS|·|\phi|)
O(∣TS∣⋅∣ϕ∣)


























 444
444

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








