Dirichlet kernel and Fejer Kernel and their convergency

最新推荐文章于 2025-05-04 23:33:02 发布

给阿姨倒一杯Cappuccino

最新推荐文章于 2025-05-04 23:33:02 发布

阅读量554

点赞数

分类专栏： BVP(p偏微分方程边界值问题) 文章标签：傅立叶分析算法

本文链接：https://blog.csdn.net/Cappucccccino/article/details/106612391

版权

Dirichlet kernel and Fejer Kernel

Considered the convergence of Fourier series (or more precisely, the N-th sum SNf) of f (under some diﬀerentiability assumptions on f, essentially we need the existence of f0). This problem shows how to improve this convergence to the case without assuming the diﬀerentiability of f.

Considering square function: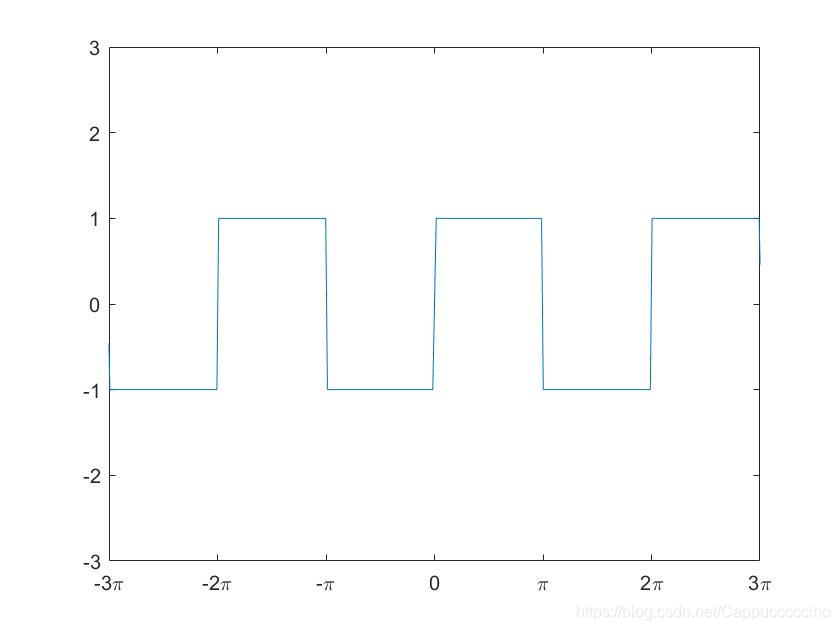 在这里插入图片描述

Using Dirichlet kernel
$D_n(x) = \frac{1}{2\pi} \sum_{k = -n}^{n}{e^{ikx}} = \frac{1}{2\pi} (1+2 \sum_{k = 1}^{n}{cos(kx)} ) = \frac{sin((n+1/2)x)}{2\pi sin(x/2)}$