文章目录
JAVA & 完美计算器
前言:
- 我设计的计算器用到的一些知识储备有:
- javase 基础语法
- java数据结构,栈的知识(部分集合类)
- 中缀表达式
- 逆波兰后缀表达式
- 思想(字符串 -> 中缀 -> 逆波兰 -> 结果)
- 优化调修
- 计算器基本用处:
- 十进制运算通用,其他进制只支持进制转化功能
- 计算复杂字符串(高复合括号,处理优先级,处理多位小数)
- 包含(+ -)<(* / % ^)(位操作符不包含,三角函数操作符不考虑),默认 * / % ^ 优先级一样
- 获取上一次的数据以及查看历史记录的功能
接下来一步步来设计我们的计算器吧!
① 我们要了解什么是中缀表达式与逆波兰后缀表达式
-
中缀表达式
- 其实就是我们平时写的表达式如: -1 / (-11 * 22) + 6 ^ 2 % 3
- 正常的序列,符号一般在数字与数字中间,除了符号表示负数时,带括号
- 补充一说,实际上一个是没两个式子就有一个括号
- 例如上面那个式子应该是:> ((-1 / (-11 * 22)) + ((6 ^ 2 )% 3))
-
逆波兰后缀表达式
- 这类表达式是专门去计算的,特定计算后就是正确结果
- 格式错误甚至报错,顺序错误大概率影响正确结果甚至报错
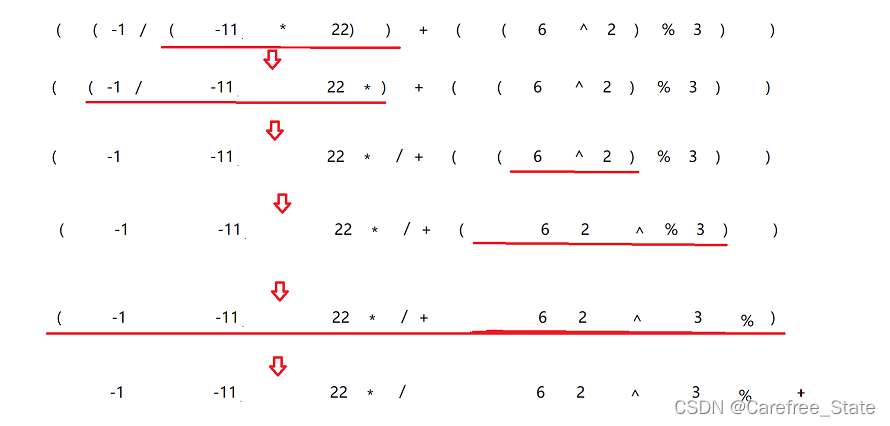
- 其实就是让中缀表达式(括号全在的情况下),将 从里往外,从左往右 把运算符往括号右边放,并且删除括号(也可最后一起删除,反正要记住那些部分是整体)

② 接下来是将字符串转化为中缀表达式
-
待处理问题:(正常人输入情况下!)
- 字符串是否带空格
- 字符串为连续,怎么确定 值与符号
- 负号代表运算还是值呢?
-
思想:
-
字符串空格在java中可以用字符串自带函数,将字符串空格转化为空字符,完成删除
replaceAll(String , String)
-
遍历一次,每次遇到数字或者小数点时循环将整个数值制作成字符串就行,其他字符就直接做成字符串
-
只需要判断每个负号前面的情况就好:
- 要么没有字符 负值
- 要么为左括号 负值
- 要么为右括号 和 数字 运算符
- 最后将负号改成 -1 * 即可
-
-
最终放进顺序表或者链表中
//记得导包!
//所有都用static是因为互相使用方便,并且这个方法不需要new一个对象才能使用,通过类名就足够了
public static List<String> transform(String s) {
//1. 去空格
s = s.replaceAll(" ", "");
//2. 存放各元素
List<String> list = new ArrayList();//存储中序表达式
int i = 0;
char c;
do {
if (((c = s.charAt(i)) < 48 || (c = s.charAt(i)) > 57)) {
list.add("" + c);
i++;
} else {
//这里是为了提高效率用了 StringBuilder
//因为本质上字符串相加调用了这个,那么我们多次相加就多次调用,还不如只调用一次!
StringBuilder stringBuilder = new StringBuilder();
while ((i < s.length() && ((c = s.charAt(i)) >= 48 && (c = s.charAt(i)) <= 57))
|| (i < s.length() && (c = s.charAt(i)) == '.')) {
stringBuilder.append(c);
i++;
}
list.add(stringBuilder.toString());
}
} while (i < s.length());
//3. 对特殊负号进行修改
for (int j = 0; j < ls.size(); j++) {
if(list.get(j).equals("-") && (j == 0 || (j > 0 && list.get(j - 1).equals("(")))) {
list.set(j, "-1");
list.add(j + 1, "*");
}
}
return list;
}
③ 中序表达式转化为逆波兰表达式
-
面临的问题:
- 优先级怎么处理
- 怎么排出正确的序列,在括号缺失,括号存在的情况下
-
处理:
- 可以写一个方法,判断符号优先级,优先级大的返回值更大 (括号优先级为最小,这里与后面的操作很重要)
- 用栈去处理!【随后解释】
- 其实我们不难想出,可以用递归,递归进一层一层括号内,但是递归每次的空间都不一样,不易操作
- 用栈去实现“倒回的思想”,先弹入的符号,后弹出,模拟出中序表达式中先里面的括号符号弹出,外面括号的符号弹出
-
有一个新的集合存放逆波兰表达式(能在原来的那个平移操作,那真的牛)
一. 优先级的处理:
当然也可以用switch( String ) 【switch在java中是可以分支字符串的】
public static int getValue(String s) {
if (s.equals("+")) {
return 1;
} else if (s.equals("-")) {
return 1;
} else if (s.equals("*")) {
return 2;
} else if (s.equals("/")) {
return 2;
} else if (s.equals("^")) {
return 2;
} else if (s.equals("%")) {
return 2;
} else {
return 0;
}
}
二.我自己做的栈实现,这里功能方便展示(也可以用java现成的集合类):
public class MyStack {
private List<String> list;
private int size;//已有元素个数
public String top;//栈顶元素
//构造方法
public MyStack() {
list = new ArrayList();
size = 0;
top = null;
}
//获取栈已有元素个数
public int size() {
return size;
}
//压栈
public void push(String s) {
list.add(s);
top = s;
size++;
}
//弹出栈顶
public String pop() {
String s = list.get(size - 1);
list.remove(size - 1);
size--;
top = size == 0 ? null : list.get(size - 1);
return s;
}
}
三.转化为逆波兰表达式:
一.获得中缀表达式
List<String> listStr = transform(s);
二. 处理中缀表达式(结合代码观看,以及结合前面的图)
-
遍历表,识别字符串的种类
- 双精度浮点型的匹配(包含负数整数小数,最全面)(^(-?\d+)(\.\d+)?$ 双精度浮点型是正则表达式),matches(正则表达式)来判断字符串是否是对应种类的数据。【当然识别字符不是负号,并且第一个字符是数字字符or负号也是OK的】
- 左括号
- 右括号
- 运算符(在我们之前的操作,负号已经全是操作符了)
-
※ 进行不同操作 【特别重要】
-
对于数值,直接放入 集合 retList 里面就好。
-
对于左括号
- 压入栈中
-
对于右括号
- 将栈中不是左括号的全部弹入 retList 中
- 最终将左括号弹出
- 左右括号这套操作,可以使得,在遇到右括号时,将这对括号内的整体进行了操作,也就是完成分割
- 也就是说,数值的顺序是一定的,运算符进入集合 retList 的时机最为重要,而左右括号这套操作,让整个表达式有条不紊的进行了, 让括号在栈中进行分割,让括号内部不干扰外部的
- 提高栈中的符号管理!
-
对于运算符,想象这么一个场景 (#¥@%¥%¥%@) ==》 (()----()----()----()… ) 一个括号式子中实际应该是这个的,
- 此次运算符的优先级小于等于栈顶优先级,就得弹入retList中(循环)
- 如果栈顶为2,此时为1 --》 这就相当于【前面的整体括号式子已经结束了,该加减后面的整体括号式子了】1 别忘了最后压栈。
* 例如,5*5 + 1 ,5/6 + 1 - 如果栈顶为1, 此时为2–》直接压栈,意味着数值应该先进行该操作。
- 如果栈顶为1/2, 此时与其相等,应该悉数弹入retList中,优先级相同,可以连续进行,既然是连续进行,那么相当于左边整体括号式子结束,别忘了最后压栈。
- 如果栈顶为0,则直接压栈即可。
- 如果栈顶为2,此时为1 --》 这就相当于【前面的整体括号式子已经结束了,该加减后面的整体括号式子了】1 别忘了最后压栈。
- 此次运算符的优先级小于等于栈顶优先级,就得弹入retList中(循环)
-
-
最终将栈中剩余的全部弹入retList中(栈顶弹出,满足思想)
public static List<String> parse(String s) {
List<String> listStr = transform(s);
List<String> retList = new ArrayList<>();
for (String ss : listStr) {
if (ss.matches("^(-?\\d+)(\\.\\d+)?$")) {
retList.add(ss);
} else if (ss.equals("(")) {
ms1.push(ss);
} else if (ss.equals(")")) {
while (!ms1.top.equals("(")) {
retList.add(ms1.pop());
}
ms1.pop();
} else {
while (ms1.size() != 0 && getValue(ms1.top) >= getValue(ss)) {
retList.add(ms1.pop());
}
ms1.push(ss);
}
}
while (ms1.size() != 0) {
retList.add(ms1.pop());
}
return retList;
}
下图以 A + ( B - D )- E / F为例的步骤剖析图:

④ 通过逆波兰表达式求结果
-
重点在于如何利用栈!【下面用到的栈是java自带的栈!】
-
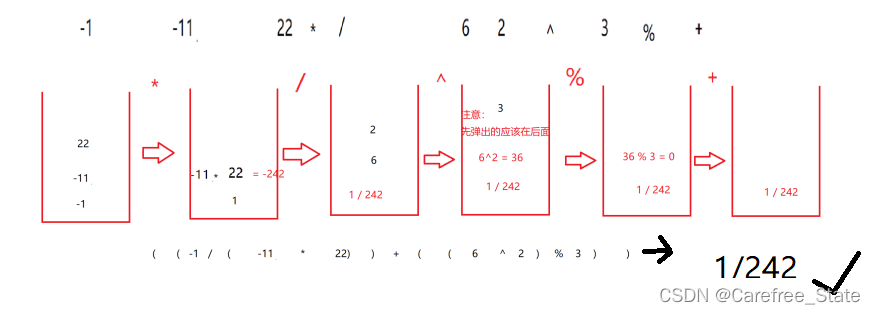
定义计算规则!【先弹出的放在右,后弹出的放在左,因为栈的特性】
-
public static void cal(Stack<String> stack, String str) { String str1 = stack.pop(); String str2 = stack.pop(); Double f1 = Double.parseDouble(str1); Double f2 = Double.parseDouble(str2); switch (str) { case "+": stack.push(f1 + f2 + ""); break; case "-": stack.push(f2 - f1 + ""); break; case "*": stack.push(f1 * f2 + ""); break; case "/": if(f1 == 0) { throw new ArithmeticException("计算"); } stack.push(f2 / f1 + ""); break; case "%" : if(f1 == 0) { throw new ArithmeticException("计算"); } if(((int)(f2 / f1))* f1 == f2) {//确定是否倍数关系的方法 stack.push(0 + ""); }else { stack.push(f2 % f1 + ""); } break; case "^": stack.push(Math.pow(f2, f1) + ""); break; }- 这里要确定倍数关系在去取模
- 是因为计算机在储存小数是,是按照一定精确度的,所以取模的时候,可能存在倍数关系,但是结果又不是0,就是因为偏差了那0.00000000001
- 这里要确定倍数关系在去取模
-
-
栈模拟出来那种“套娃”,说到底就是运算“到底”,两个数就通过运算符结合成一个数,直到最后一个数
- 遍历集合,一直压栈直到遇到符号,就“融合”前面两个数,然后继续直到集合末尾
如下图所示:
public static String calculate(String s) {
List<String> arrayList = reversePolish.parse(s);
Stack<String> stringStack = new Stack<>();
for (int i = 0; i < arrayList.size(); i++) {
String str = arrayList.get(i);
if(str.equals("+") || str.equals("-") || str.equals("*") || str.equals("/") || str.equals("^") || str.equals("%")) {
cal(stringStack, str);//cal为刚才的计算原理
}else {
stringStack.push(str);
}
}
return stringStack.pop();
}
这里埋个伏笔,返回的是字符串,因为我们不仅仅要用到它的值,还要它的字符串。
只需要将字符串转化为double型(用java中String自带的方法)就好了【也可遍历字符串去慢慢构建一个double型也行】
⑤ 计算器搭建组装
一.菜单以及初步框架
public static void menu() {
System.out.println("***********### 计算器 ###************");
System.out.println(" 1. 获取上一次的值继续运算");
System.out.println(" 2. 重新开始计算");
System.out.println(" 3. 进制转化(只限整数)");
System.out.println(" 4. 获取上一次的n进制序列");
System.out.println(" 5. 查看历史记录");
System.out.println(" 0. 退出");
System.out.println("****************************************");
System.out.print("请选择:> ");
}
String str = "";
Scanner scanner = new Scanner(System.in);
PrevNum prevNum = new PrevNum();
List<String> history = new ArrayList<>();
int input = 0;
do {
menu();
input = scanner.nextInt();
scanner.nextLine();
switch (input) {
case 1:
//区域1
break;
case 2:
//区域2
break;
case 3:
//区域3
break;
case 4 :
//区域4
break;
case 5:
//区域5
break;
case 0:
//区域6
break;
default:
//区域7
break;
}
}while(input != 0);
}
二.各个组件【代码基本部分阅读简单,不作赘述】
public class 你他妈脑子异常 extends RuntimeException{
public 你他妈脑子异常() {
}
public 你他妈脑子异常(String message) {
super(message);
}
}
为了对一些无脑操作痛击!!!而设计的异常(汉字可以做类名,但是不合理(像触发这个异常的操作者一样),我们应该有正确的写代码风格)
-
组件1区域1:
-
System.out.print("请输入:> " + str); str += scanner.nextLine(); String s1 = str; str = calculate(str); System.out.println("=" + Double.parseDouble(str)); history.add(s1 + " = " + Double.parseDouble(str)); -
获取上一次的值继续运算(那个计算后的字符串被记录下来了,这样就可以追加续写了)
-
-
组件2区域2:
-
System.out.print("请输入:> "); str = scanner.nextLine(); String s2 = str; str = calculate(str); System.out.println("=" + Double.parseDouble(str)); history.add(s2 + " = " + Double.parseDouble(str)); -
重新开始计算
-
-
组件3区域3:
-
class PrevNum { String string; int radix; public PrevNum() { } public PrevNum(String string, int radix) { this.string = string; this.radix = radix; } public int getValue() { return Integer.parseInt(string, radix); } public void set(String string, int radix) { this.string = string; this.radix = radix; } @Override public String toString() { if (string == null) { throw new 你他妈脑子异常("明明没有上一个");//自制的异常 } return "数值为 '" + string + '\'' + ", 进制为 " + radix; } } -
为记录上一个n进制序列设计的一个类
-
System.out.print("请输入你接下来输入的数的进制:>"); int r = scanner.nextInt(); scanner.nextLine(); System.out.print("请输入整数对应的" + r + "进制数:> "); int number = scanner.nextInt(r); scanner.nextLine(); System.out.print("请输入你要转化为进制[2, 36]:> "); int radix = scanner.nextInt();//括号内输入radix,代表输入什么进制的 scanner.nextLine(); String string1 = Integer.toString(number, radix); System.out.println("转化成功:> " + string1); history.add(Integer.toString(number, r) + " = " + string1 + " (" + r + "->" + radix + ")"); prevNum.set(string1, radix); -
进制转化(只限整数)
-
-
组件4区域4:
-
System.out.println(prevNum); System.out.print("请输入你要转化为进制[2, 36]:> "); int newRadix = scanner.nextInt(); scanner.nextLine(); String string2 = Integer.toString(prevNum.getValue(), newRadix); System.out.println("转化成功:> " + string2); history.add(prevNum.string + " = " + string2 + " (" + prevNum.radix + "->" + newRadix + ")"); prevNum.set(string2, newRadix); -
获取上一次的n进制序列
-
-
组件5区域5:
-
System.out.println("================================================"); if(history.size() == 0) { System.out.println("空"); }else { for(String s : history) { System.out.println("💖 " + s); } } System.out.println("================================================"); -
查看历史记录
-
-
组件0区域6:
-
System.out.println("退出成功"); -
退出
-
-
组件defau区域7:
-
throw new 你他妈脑子异常(" 艹 "); -
对不正当操作的抨击
-
测试
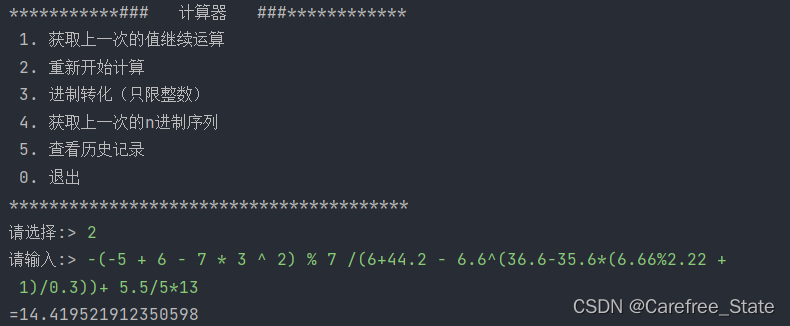
下面是手动结合机动运算检测:

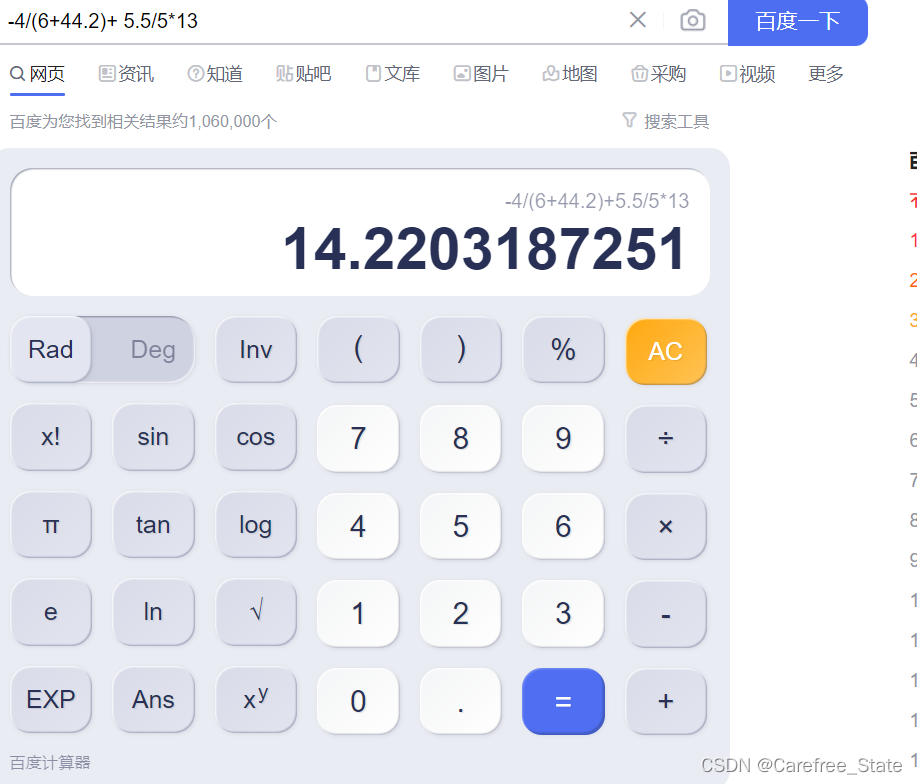
这里我省略了
因为这一部分很接近0,省略一部分数导致的偏差。
复杂表达式验算成功!
文章到此结束!谢谢观看 ,关注我,看更多优质文章!
可以叫我 小马,我可能写的不好或者有错误,但是一起加油鸭🦆!这是我的代码仓库!(在马拉圈的23.2里)代码仓库 ,计算器最终版仓库具体位置)
邮箱:2040484356@qq.com
就是因为优先级或者括号组在一起的式子。 ↩︎























 471
471











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










