金罐游戏的两种动态规划解法

问题描述

金罐游戏中有两个玩家，A和B，所有的金罐排成一排，每个罐子里都有一些金币， 玩家可以看到每个金罐中有多少硬币。A和B两个玩家交替轮流打开金罐，但是必须从一排的某一端开始挑选，玩家可以从一排罐的任一端挑选一个罐打开。 获胜者是最后拥有更多硬币的玩家。 我们是A玩家，问如何才能使A 收集的硬币数量最大。
假设 B 也是按照“最佳”策略玩，并且 A 开始游戏。

示例：[4,6,2,3]
拿取顺序

金罐中金币个数（已排列）	A	B
4, 6, 2, 3	3
4, 6, 2		4
6, 2	6
2		2
	9 coins	6 coins

类似的问题：
Leetcode 486题 预测赢家

给你一个整数数组 nums 。玩家 1 和玩家 2 基于这个数组设计了一个游戏。

玩家 1 和玩家 2 轮流进行自己的回合，玩家 1 先手。开始时，两个玩家的初始分值都是 0 。每一回合，玩家从数组的任意一端取一个数字（即，nums[0] 或 nums[nums.length - 1]），取到的数字将会从数组中移除（数组长度减 1 ）。玩家选中的数字将会加到他的得分上。当数组中没有剩余数字可取时，游戏结束。

如果玩家 1 能成为赢家，返回 true 。如果两个玩家得分相等，同样认为玩家 1 是游戏的赢家，也返回 true 。你可以假设每个玩家的玩法都会使他的分数最大化。

解题思路

Step1：穷举

首先，不考虑双方需要采取的策略，穷举所有的可能。红色为A能获得金币数，蓝色为B能获得的金币数。此时，理论上来说A最多能拿到10个。

但考虑双方都采取最优策略后，“A能拿到10个金币”这种可能实际上并不会发生。下面我们自底向上进行分析。

Step2：从len(pots)=1到len(pots)=4

首先，如果子列中仅有1个元素，当前玩家只能选择该元素。

如果子列中有2个元素，当前玩家一定选择较大的。例如，子列为[2,3]时，A一定选择3。

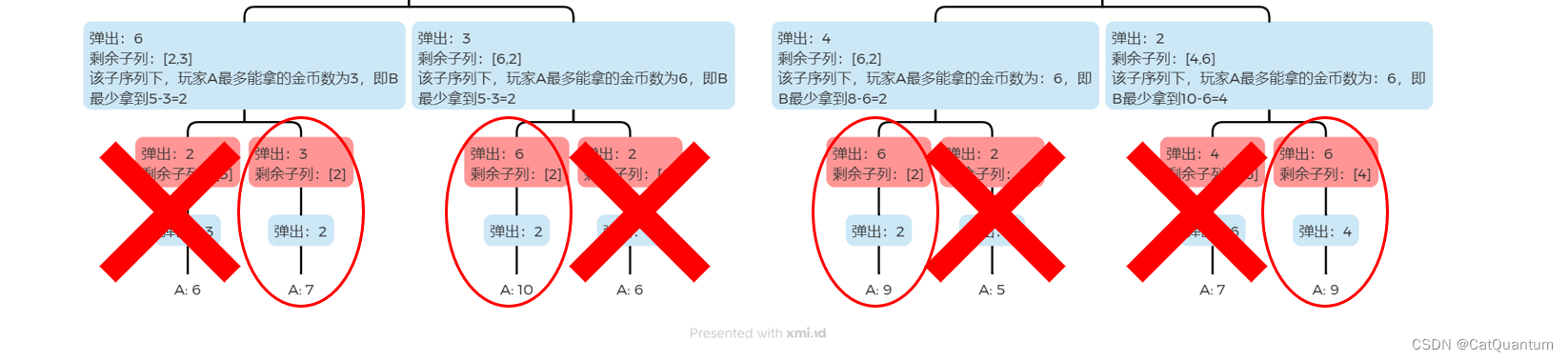
如果子列中有3个元素，B做出选择后，A能得到的金币数也就确定了。例如，子列为[6,2,3]时，B选6（左边），剩余[2,3]，那么A接下来一定会选3，B选2；如果B选3，剩余[6,2]，那么A接下来一定会选6，B选2。

即，B最多能拿到的金币数为$max(6+(剩余总金币-A得到的)，3+(剩余总金币-A得到的)))$。而$(剩余总金币-A得到的)$，实际上就是B第二次选择时能得到金币数。
最终我们得到$max(6+2,3+2)=8$，选左边。

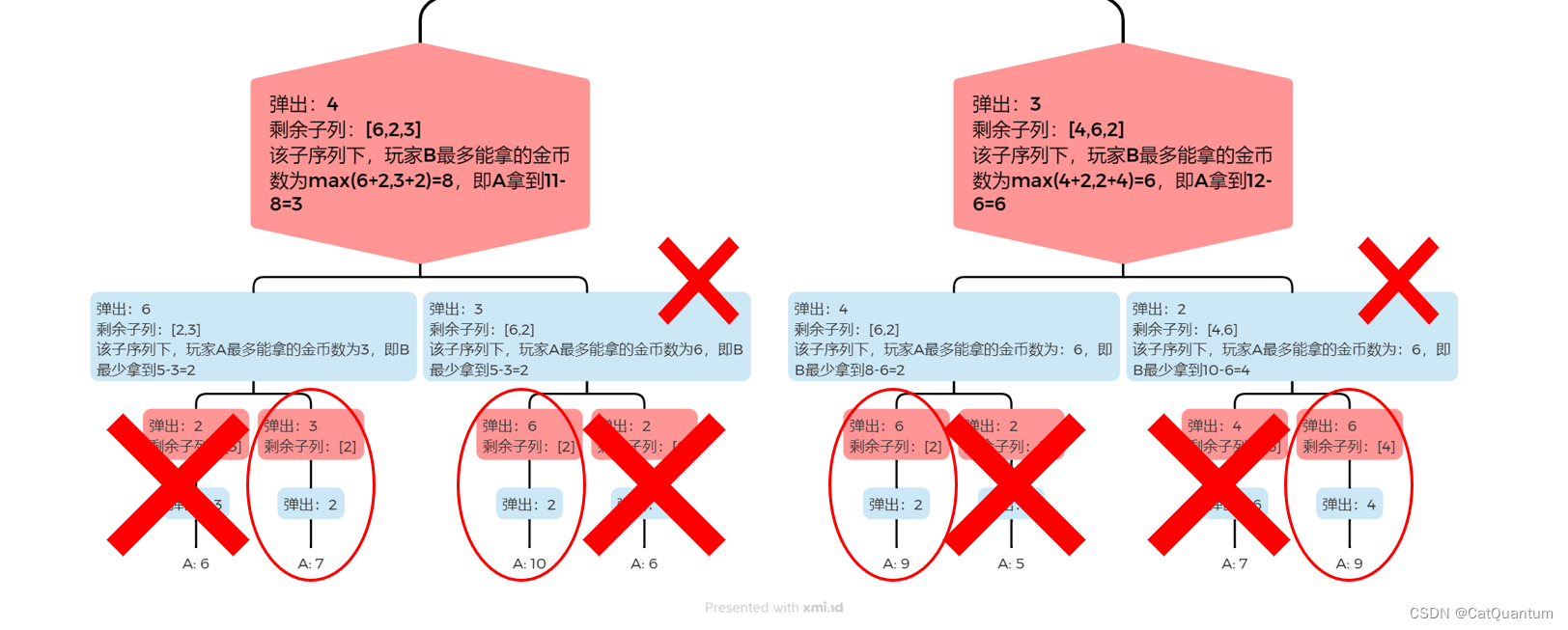
如果子列中有4个元素，计算过程与子列中有3个元素类似。
$$\begin{gathered} max(4+(剩余总金币-B得到的)，3+(剩余总金币-B得到的))) \\ =max(4+3,3+6) \\ =9 \end{gathered}$$

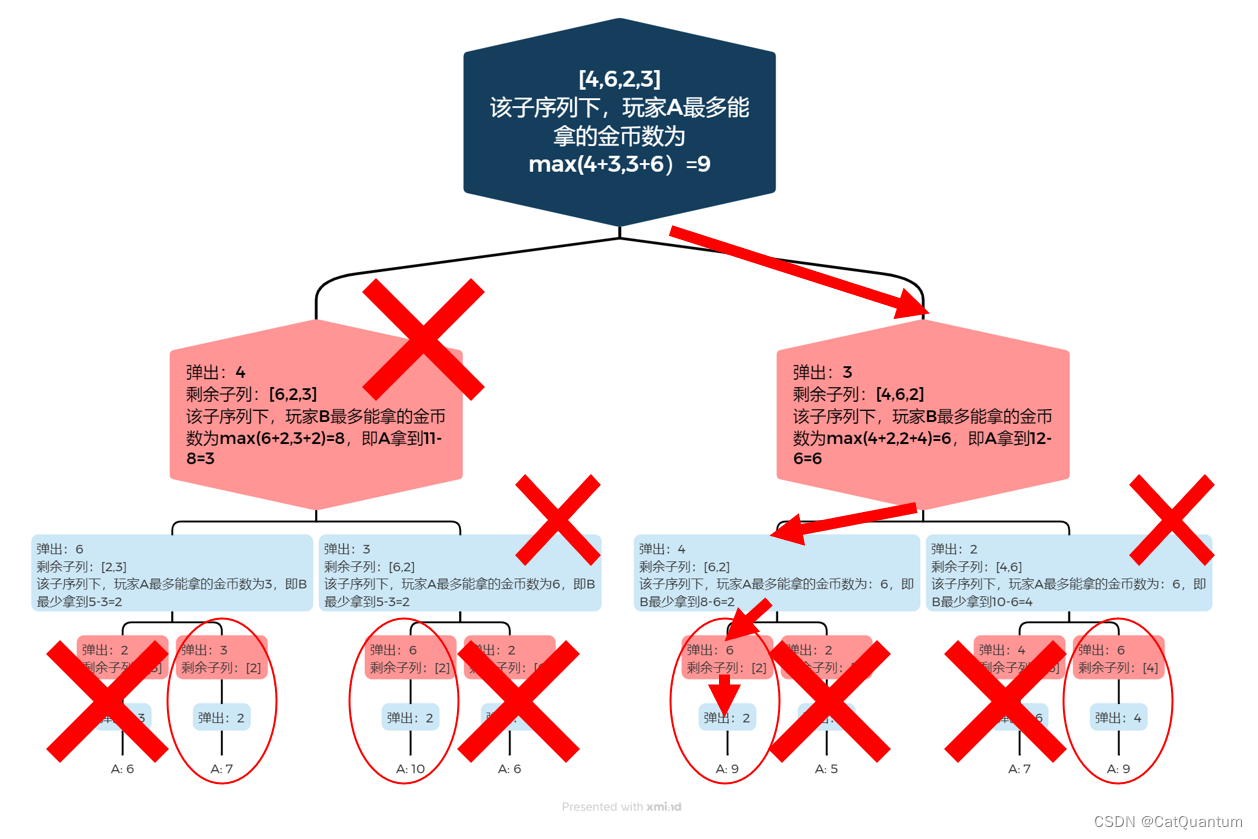
Step3: 拓展，更一般化的表述

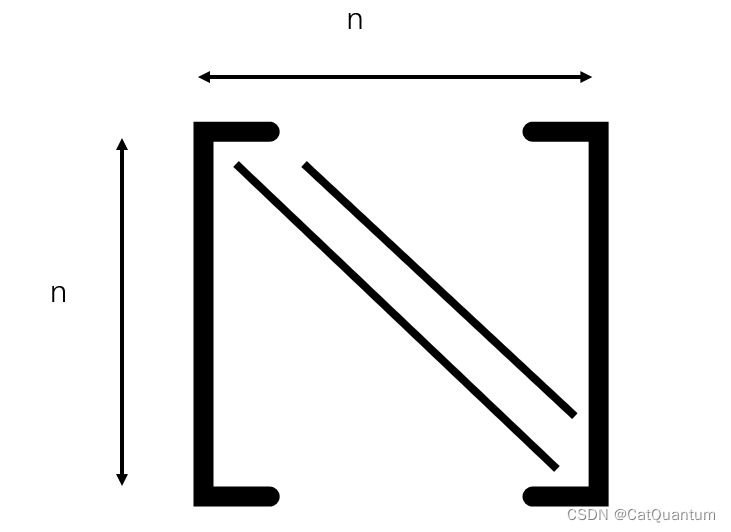
那么现在，假设[4,6,2,3]是更大的金罐序列pots的一部分，pots[i]=4,pots[j]=3，len(pots)=n

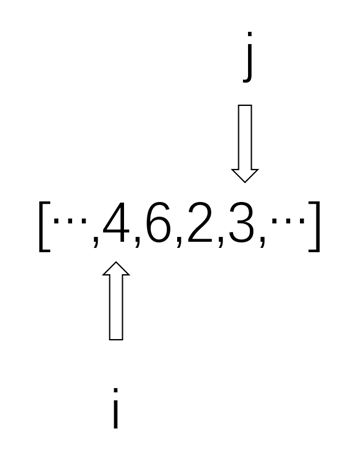
如图所示，每当我们选择左边的罐子，i右移一格；每当我们选择右边的罐子，j左移一格。

假设 $dp[i][j]$表示当金罐子序列从第 i 个到第 j 个时，当前操作的玩家（假设为A）可以从这些金罐中获得的最大金币数。
如果A取第i个罐子，则对方从剩下的金罐中获得的最大金币数为$dp[i+1][j]$。
此时A获得的金币为：$pots[i]+(total[i][j-1]-dp[i][j-1])$
接下来B进行选择，两种选择分别导向A得到$dp[i+2][j]$，或 $dp[i+1][j-1]$，B一定是选择让A最少的，即$min(dp[i+2][j],dp[i+1][j-1])$
即，此时A获得的金币为：
$$pots[i]+min(dp[i+2][j],dp[i+1][j-1])$$

同理，如果A取第j个罐子，A获得的金币为：
$$pots[j]+min(dp[i+1][j-1],dp[i][j-2])$$

那么A是取第 i 还是第 j 个罐子？当然是较大的那个选择。即：
$$\begin{gathered} max(pots[i]+min(dp[i+2][j],dp[i+1][j-1]), \\ pots[j]+min(dp[i+1][j-1],dp[i][j-2]) \end{gathered}$$
这就是我们的状态转移方程。
很明显，至少有三个罐子时，这个方程才行得通。即边界条件为：
边界条件：
$i=j$(一个罐子)：$$dp[i][i]=pots[i]$$
$i+1=j$(两个罐子)：$$dp[i][j]=max(pots[i],pots[j])$$

Step4:算法实现

很明显$dp[i][j]$可以用一个$n\times n$的二维数组表示。计算过程就是先把pots[i]填充到对角线（边界条件1），再依次比较相邻两个元素的较大值填充到次对角线（边界条件2），接着依次填充右上方的矩阵。时间复杂度和空间复杂度都为$O(n^2)$。通过三角矩阵的压缩存储可以降低存储空间占用（$n^2\to \frac{n(n+1)}{2}$），但空间复杂度依然为$O(n^2)$

只计算能得到的最大金币数：

def max_coins(pots):
    n = len(pots)
    # 创建一个 n x n 的二维列表，初始化为 0
    dp = [[0] * n for _ in range(n)]
    
    # 处理只有一个金罐的情况
    for i in range(n):
        dp[i][i] = pots[i]
    
    # 处理有两个金罐的情况
    for i in range(n - 1):
        dp[i][i + 1] = max(pots[i], pots[i + 1])
    
    # 使用动态规划填充 dp 表
    for length in range(3, n + 1):  # 从长度为 3 到 n
        for i in range(n - length + 1):
            j = i + length - 1
            # 计算两种情况，选择最优解
            pick_first = pots[i] + min(dp[i + 2][j] if i + 2 <= j else 0,
                                       dp[i + 1][j - 1] if i + 1 <= j - 1 else 0)
            pick_last = pots[j] + min(dp[i + 1][j - 1] if i + 1 <= j - 1 else 0,
                                      dp[i][j - 2] if i <= j - 2 else 0)
            dp[i][j] = max(pick_first, pick_last)
    
    # 最终结果存储在 dp[0][n-1] 中
    return dp[0][n - 1]

# 示例
pots = [4, 6, 2, 3]
print(max_coins(pots))  # 输出应为玩家 A 可以获得的最大硬币数

记录选择：

def max_coins_with_tracking(pots):
    n = len(pots)
    dp = [[0] * n for _ in range(n)]
    # 用于记录每一步的选择路径
    pick = [[None] * n for _ in range(n)]
    
    for i in range(n):
        dp[i][i] = pots[i]
        pick[i][i] = (i, 'take only pot')

    for i in range(n - 1):
        if pots[i] > pots[i + 1]:
            pick[i][i + 1] = (i, 'take leftmost pot')
        else:
            pick[i][i + 1] = (i + 1, 'take rightmost pot')
        dp[i][i + 1] = max(pots[i], pots[i + 1])
    
    for length in range(3, n + 1):
        for i in range(n - length + 1):
            j = i + length - 1
            
            left_option = min(dp[i + 2][j] if i + 2 <= j else 0, dp[i + 1][j - 1] if i + 1 <= j - 1 else 0)
            right_option = min(dp[i + 1][j - 1] if i + 1 <= j - 1 else 0, dp[i][j - 2] if i <= j - 2 else 0)
            pick_first = pots[i] + left_option
            pick_last = pots[j] + right_option
            
            if pick_first > pick_last:
                dp[i][j] = pick_first
                pick[i][j] = (i, 'take leftmost pot')
            else:
                dp[i][j] = pick_last
                pick[i][j] = (j, 'take rightmost pot')

    # 回溯选择路径
    choices = []
    i, j = 0, n - 1
    while i <= j:
        choice_index, choice_description = pick[i][j]
        choices.append((choice_index, choice_description))
        if choice_description == 'take leftmost pot':
            i += 1
        else:
            j -= 1

    return dp[0][n - 1], choices,pick

# 示例
pots = [4, 6, 2, 3]
max_coins, choices ,pick= max_coins_with_tracking(pots)
print("Maximum coins:", max_coins)
print("Choices:")
for index, choice in choices:
    print(f"Pot {index + 1} with {pots[index]} coins: {choice}")

另一种解题思路

另一种思路来自于CSND上“很咸的飞鱼”的这篇帖子：金罐游戏
这个解法，将区间$[i,j]$的罐子中先手玩家与后手玩家最终得到的金币数量的差值设为$dp[i][j]$，动态规划方程为：
$$\mathrm{dp}[\mathrm{i}][\mathrm{j}]=\max (\mathrm{coins}[\mathrm{i}]-\mathrm{dp}[\mathrm{i}+1][\mathrm{j}],\mathrm{coins}[\mathrm{j}]-\mathrm{dp}[\mathrm{i}][\mathrm{j}-1])$$
这种解法不直接计算得到的最大金币数，而是从博弈的角度，在零和游戏里拉大分差。因为在这个游戏里，A拿的多B就拿得少，一个玩家的收益就是另一个玩家的损失。
相应的，动态方程的含义为：
$$\begin{gathered} 最终相比于对方的分差= \\ 选择i/j能得到的分数-这样选择后对方会获得多少优势 \end{gathered}$$
例如:
对于[2,3]，A的选择为max(2-3,3-2)=1，所以选右边，得到3个金币，比B多1。
对于[6,2,3]，B选左边，则得到6个金币，而这样选择的话，接下来A会比B多1个金币，最终分差为6-1=5，B比A多5个；同理，选右边，则为3-4=-1，B比A多-1个，也就是比A少1个。故max(6-1,3-4)=5

最大化两者间的差距（这里设置的$dp[i][j]$）和最大化收益（得到的金币数，也就是下图的$A_{max}$）是可以相互转化的。

$$A_{max}=A_{max}^{\prime }+coin(i/j)$$
$$\begin{gathered} dp[i][j]=A_{max}-B_{max} \\ =A_{max}^{\prime }+coin(i/j)-Bmax \\ =-(Bmax-A^{\prime }max)+coin(i/j) \\ =coin(i/j)-dp[i+1][j]/dp[i][j-1] \end{gathered}$$
注：A’是第二轮时A的选择，也就是（第一轮）A选择→B选择→（第二轮）A选择→…

该方法的代码实现、效率等，详见原文。