SciPy是什么？是一个开源的 Python 算法库和数学工具包

​​SciPy​​ 是一个基于 Python 的开源科学计算库，构建在 ​​NumPy​​ 的基础之上，提供了大量高效且易于使用的数学算法和工具，用于解决科学计算、工程建模、数据分析等领域的问题。它是 Python 科学计算生态系统的核心组成部分之一。

---

​​SciPy 的主要功能模块​​

SciPy 包含多个子模块，覆盖不同领域的数学和工程问题：

1. ​​优化（scipy.optimize）​​：函数最优化、方程求解、曲线拟合。
2. ​​积分（scipy.integrate）​​：数值积分、常微分方程求解。
3. ​​线性代数（scipy.linalg）​​：矩阵分解、特征值计算、线性方程组求解。
4. ​​信号处理（scipy.signal）​​：滤波、频谱分析、波形生成。
5. ​​统计（scipy.stats）​​：概率分布、假设检验、描述性统计。
6. ​​插值（scipy.interpolate）​​：数据插值、样条曲线拟合。
7. ​​图像处理（scipy.ndimage）​​：图像滤波、形态学操作、特征提取。
8. ​​稀疏矩阵（scipy.sparse）​​：高效存储和操作稀疏矩阵。
9. ​​空间算法（scipy.spatial）​​：几何计算、空间索引（如 KD-Tree）、聚类。

---

 

​​主要应用场景​​

1. ​​科学研究与工程建模​​

   • 物理模拟（如流体力学、热传导）、结构分析、信号处理（音频/图像处理）。
   • 例如：使用 scipy.integrate 求解微分方程模拟物理系统。

2. ​​数据科学与机器学习​​

   • 数据预处理（插值、标准化）、统计分析、特征工程。
   • 例如：使用 scipy.stats 进行假设检验或生成概率分布。

3. ​​优化与控制​​

   • 参数调优、最优化问题（如最小化损失函数）、控制系统设计。
   • 例如：使用 scipy.optimize.minimize 求解非线性优化问题。

4. ​​图像和信号处理​​

   • 图像去噪、滤波（如低通/高通滤波）、频谱分析。
   • 例如：使用 scipy.signal 设计数字滤波器。

5. ​​数值计算与算法实现​​

   • 线性代数运算（如矩阵求逆）、特殊函数计算（如贝塞尔函数）、稀疏矩阵运算。
   • 例如：使用 scipy.linalg 计算矩阵特征值。

6. ​​教育与原型开发​​

   • 快速验证数学模型或算法，适用于教学和科研原型设计。

---

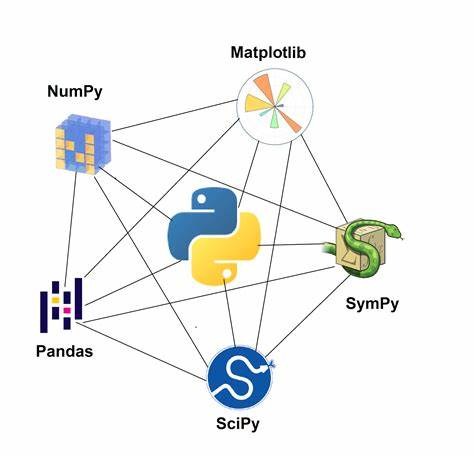
​​与其他库的协作​​

• ​​NumPy​​：SciPy 依赖 NumPy 数组作为基础数据结构。
• ​​Matplotlib​​：常与 SciPy 配合进行数据可视化。
• ​​Pandas​​：处理表格数据后，可用 SciPy 进行高级分析。
• ​​Scikit-learn​​：在机器学习中，SciPy 提供底层数学支持。

---

​​总结​​

SciPy 是 Python 中解决复杂数学问题和工程计算的核心工具，尤其适合需要高性能数值计算的场景。无论是学术研究、工业开发还是数据分析，SciPy 都能提供高效的算法支持，是科学计算领域的“瑞士军刀”。

---

​​使用 SciPy 求解 ​​一维热传导方程​​ 的完整示例

import numpy as np
import matplotlib.pyplot as plt
from scipy.sparse import diags
from scipy.sparse.linalg import spsolve

plt.rcParams['font.sans-serif'] = ['SimHei']  # 设置中文字体
plt.rcParams['axes.unicode_minus'] = False    # 解决负号显示异常:ml-citation{ref="4,6" data="citationList"}


# 参数设置
L = 10.0          # 材料长度 (m)
nx = 50          # 空间网格点数
dx = L / (nx-1)  # 空间步长
nt = 100         # 时间步数
dt = 0.001       # 时间步长
alpha = 1e-4     # 热扩散系数 (m²/s)

# 稳定性条件检查（显式法需满足 alpha*dt/dx² < 0.5）
print(f"CFL条件是否满足: {alpha*dt/dx**2 < 0.5}")  # 输出 True 表示稳定

# 初始化网格和温度场
x = np.linspace(0, L, nx)
u = np.zeros(nx)
u[0] = 100.0      # 左端固定温度 100°C
u[-1] = 0.0       # 右端固定温度 0°C

# 构建离散化的二阶导数矩阵（三对角稀疏矩阵）
A = diags([-1, 1], [-1, 1], shape=(nx, nx)).toarray()
A = A / dx**2     # 离散化系数

# 时间步进（显式欧拉法）
for _ in range(nt):
    u_new = u.copy()
    u_new[1:-1] = u[1:-1] + alpha * dt * (A[1:-1, 1:-1] @ u[1:-1])
    u = u_new

# 可视化结果
plt.figure(figsize=(10, 6))
plt.plot(x, u, label=f't={nt*dt:.3f}s')
plt.xlabel('位置 x (m)')
plt.ylabel('温度 u (°C)')
plt.title('一维热传导方程数值解')
plt.legend()
plt.grid(True)
plt.show()