1.水壶问题
https://leetcode-cn.com/problems/water-and-jug-problem/
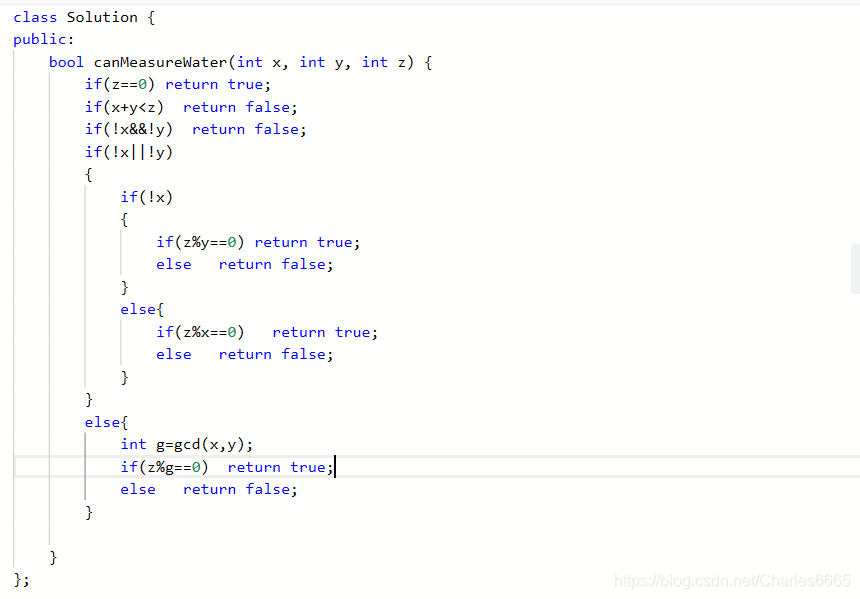
裴蜀定理(或贝祖定理)得名于法国数学家艾蒂安·裴蜀,说明了对任何整数a、b和它们的最大公约数d,关于未知数x和y的线性不定方程(称为裴蜀等式):若a,b是整数,且gcd(a,b)=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别地,一定存在整数x,y,使ax+by=d成立。
它的一个重要推论是:a,b互质的充要条件是存在整数x,y使ax+by=1.
 本文深入探讨裴蜀定理(贝祖定理),解析整数a、b及其最大公约数d的关系,强调当a、b互质时,存在整数x、y使ax+by=1。并结合水壶问题实例,展示裴蜀定理的实际应用。
本文深入探讨裴蜀定理(贝祖定理),解析整数a、b及其最大公约数d的关系,强调当a、b互质时,存在整数x、y使ax+by=1。并结合水壶问题实例,展示裴蜀定理的实际应用。
1.水壶问题
https://leetcode-cn.com/problems/water-and-jug-problem/
裴蜀定理(或贝祖定理)得名于法国数学家艾蒂安·裴蜀,说明了对任何整数a、b和它们的最大公约数d,关于未知数x和y的线性不定方程(称为裴蜀等式):若a,b是整数,且gcd(a,b)=d,那么对于任意的整数x,y,ax+by都一定是d的倍数,特别地,一定存在整数x,y,使ax+by=d成立。
它的一个重要推论是:a,b互质的充要条件是存在整数x,y使ax+by=1.

 1316
1316
 863
863

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?


