转载自https://blog.csdn.net/shenxiaolu1984/article/details/50884830
相关KCF跟踪算法讲解:
https://blog.csdn.net/shenxiaolu1984/article/details/50905283
https://www.cnblogs.com/YiXiaoZhou/p/5925019.html
Matlab代码实现:
https://blog.csdn.net/bitopyx/article/details/81948875?spm=1001.2014.3001.5502
https://blog.csdn.net/weixin_38128100/article/details/95729653
All circulant matrices are made diagonal by the Discrete Fourier Transform (DFT), regardless of the generating vector x.
任意循环矩阵可以被傅里叶变换矩阵对角化。
文献中,一般用如下方式表达这一概念:
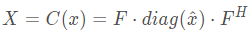
其中
X
X
X是循环矩阵,
x
^
\hat{x}
x^是原向量
x
x
x的傅里叶变换,
F
F
F是傅里叶变换矩阵,上标H表示共轭转置:
X
H
=
(
X
∗
)
T
X^H=(X^*)^T
XH=(X∗)T。
换句话说, X X X相似于对角阵, X X X的特征值是 x ^ \hat x x^的元素。
另一方面,如果一个矩阵能够表示成两个傅里叶矩阵夹一个对角阵的乘积形式,则它是一个循环矩阵。其生成向量是对角元素的傅里叶逆变换。
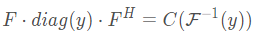
这个公式初看疑问很多,以下意义讨论。
X X X是什么?
X
X
X是由原向量
x
x
x生成的循环矩阵。以矩阵尺寸
K
=
4
K=4
K=4为例。
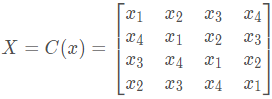
F F F是什么?
F
F
F是离散傅里叶矩阵(DFT matrix),可以用一个复数
w
=
e
−
2
π
i
/
K
w=e^{-2\pi i/K}
w=e−2πi/K表示,其中
K
K
K为方阵
F
F
F的尺寸,以
K
=
4
K=4
K=4为例。
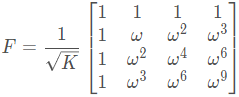
把
w
w
w想象成一个角度为
2
π
/
K
2\pi /K
2π/K的向量,这个矩阵的每一行是这个向量不断旋转。从上到下,旋转速度越来越快。
之所以称为DFT matrix,是因为一个信号的DFT变换可以用此矩阵的乘积获得:
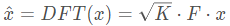
反傅里叶变换也可以通过类似手段得到:
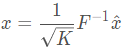
傅里叶矩阵有许多性质:
- 是对称矩阵,观察 w w w的规律即可知;
- 满足
F
H
F
=
F
F
H
=
I
F^HF=FF^H=I
FHF=FFH=I,也就是说它是个酉矩阵。
注意: F F F是常数,可以提前计算好,和要处理的 x x x无关。
对角化怎么理解?
把原公式两边乘以逆矩阵:
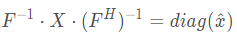
利用酉矩阵性质:
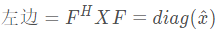
也就是说,矩阵
X
X
X通过相似变换
F
F
F变成对角阵
d
i
a
g
(
x
^
)
diag(\hat x)
diag(x^),即对循环矩阵
X
X
X进行对角化。另外,
F
H
X
F
F^HXF
FHXF是矩阵
X
X
X的2D DFT变换。即傅里叶变换可以把循环矩阵对角化。
怎么证明?
可以用构造特征值和特征向量的方法证明(参看这篇论文(Gray, Robert M. Toeplitz and circulant matrices: A review. now publishers inc, 2006.)的3.1节)。此处简单描述。
考察待证明等式的第k列:
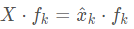
其中,
f
k
f_k
fk表示DFT矩阵的第k列,
x
^
k
\hat x_k
x^k表示傅里叶变换的第k个元素。等价于求证:
f
k
f_k
fk和
x
^
k
\hat x_k
x^k是
X
X
X的一对特征向量和特征值。
左边向量的第i个元素为:
l
e
f
t
i
=
[
x
i
,
f
k
]
left_i=[x^i,f_k]
lefti=[xi,fk]。
x
i
x^i
xi表示把生成向量
x
x
x向右移动i位,[]表示内积。内积只和两个向量的相对位移有关,所以可以把
f
k
f_k
fk向左移动i位:
l
e
f
t
i
=
[
x
,
f
k
−
i
]
left_i=[x,f_k^{-i}]
lefti=[x,fk−i]。DFT矩阵列的移位可以通过数乘
w
w
w的幂实现:
f
k
i
=
f
0
⋅
w
i
k
f_k^i=f_0\cdot w^{ik}
fki=f0⋅wik。
更多性质
利用对角化,能推导出循环矩阵的许多性质。
转置
循环矩阵的转置也是一个循环矩阵(可以查看循环矩阵各元素排列证明),其特征值和原特征值共轭。
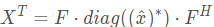
可以通过如下方式证明:
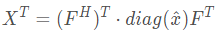
由于
F
F
F是对称酉矩阵,且已知
X
X
X是实矩阵:
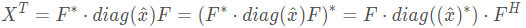
如果原生成向量
x
x
x是对称向量(例如[1,2,3,4,3,2]),则其傅里叶变换为实数,则:
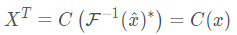
卷积
循环矩阵乘向量等价于生成向量的逆序和该向量卷积,可进一步转化为傅里叶变换相乘。注意卷积本身即包含逆序操作,另外利用了信号与系统中经典的“时域卷积,频域相乘”。
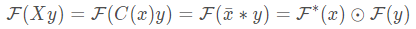
其中
x
ˉ
\bar x
xˉ表示把
x
x
x的元素倒序排列。星号表示共轭。
相乘
设
A
,
B
A, B
A,B为循环矩阵,其乘积的特征值等于特征值的乘积:
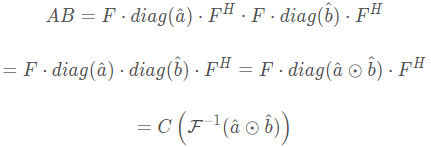
乘积也是循环矩阵,其生成向量是原生成向量对位相乘的傅立叶逆变换。
相加
和的特征值等于特征值的和。
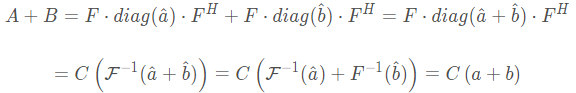
和也是循环矩阵,其生成向量是原生成向量的和。
求逆
循环矩阵的逆,等价于将其特征值求逆。
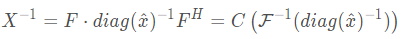
对角阵求逆等价于对角元素求逆,以下证明:
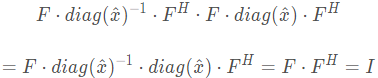
逆也是循环矩阵。
有什么用?
该性质可以将循环矩阵的许多运算转换成更简单的运算。例如:
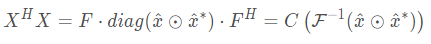
原始计算量:两个方阵相乘
(
O
(
K
3
)
)
(O(K^3))
(O(K3))
转化后的计算量:反向傅里叶
(
K
l
o
g
K
)
+
(K logK)+
(KlogK)+向量点乘
(
K
)
(K)
(K)。
CV的许多算法中,都利用了这些性质提高运算速度,例如2015年TPAMI的这篇高速跟踪KCF方法。
二维情况
以上探讨的都是原始信号为一维的情况,以下证明二维情况下的
F
H
X
F
=
d
i
a
g
(
x
^
)
F^HXF=diag(\hat x)
FHXF=diag(x^),推到方法和一维类似。
x
x
x是二维生成矩阵,尺寸
N
×
N
N\times N
N×N。
X
X
X是一个
N
2
×
N
2
N^2\times N^2
N2×N2的分块循环矩阵,其uv块记为
x
u
v
x^{uv}
xuv,表示
x
x
x下移u行,右移v列。
F
F
F是
N
2
×
N
2
N^2\times N^2
N2×N2的二维DFT矩阵,其第uv块记为
f
u
v
=
{
w
u
i
+
v
j
}
i
j
f_{uv}=\{w^{ui+vj}\}_{ij}
fuv={wui+vj}ij。
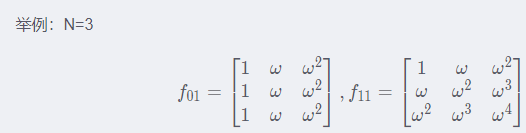
需要验证的共有
N
×
N
N\times N
N×N个等式,其中第uv个为:
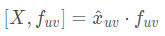
其中,
[
X
,
f
u
v
]
[X,f_{uv}]
[X,fuv]表示把
x
u
v
x^{uv}
xuv分别和
f
u
v
f_{uv}
fuv做点乘,结果矩阵元素求和。
这个等式的第ij元素为:
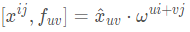
再次利用两个性质:(1)点乘只和两个矩阵相对位移有关(2)
f
u
v
f_{uv}
fuv的位移可以用乘
w
w
w幂实现:
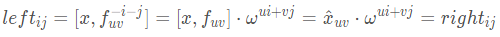
代码
以下matlab代码验证上述性质。需要注意的是,matlab中的dftmatx函数给出的结果和本文定义略有不同,需做一简单转换。另外,matlab中的撇号表示共轭转置,transpose为转置函数,conj为共轭函数。
clear;clc;close all;
% 1. diagnolize
K = 5; % dimension of problem
x_base = rand(1,K); % generator vector
X = zeros(K,K); % circulant matrix
for k=1:K
X(k,:) = circshift(x_base, [0 k-1]);
end
x_hat = fft(x_base); % DFT
F = transpose(dftmtx(K))/sqrt(K); % the " ' " in matlab is transpose + conjugation
X2 = F*diag(x_hat)*F';
display(X);
display(real(X2));
% 2. fast compute correlation
C = X'*X;
C2 = (x_hat.*conj(x_hat))*conj(F)/sqrt(K);
display(C);
display(C2);





















 1万+
1万+











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








