Manacher 回文自动机 学习笔记

Manacher

“马拉车”算法

非常好写好调的回文串算法。
用途：在$O(n)$时间内，求出以每一个点为中心的回文串长度。

首先，有一个非常巧妙的转化。由于回文串长度有可能为奇数也有可能为偶数，说明回文中心不一定在一个字符上。所以要将字符串做如下处理：在每两个字母之间插入一个特殊字符，通常用“#”，这样所有的回文串就都变成了以一个字符为回文中心的。并且，我们需要在字符串的开头或者结尾插入另一个特殊字符，比如说“*”,防止它无休止地匹配下去。

变量声明：
mx：当前已经判断过的能成为回文串的最远长度。比如说如果字符串为bacabaaa，枚举回文中心到c，那么mx应该为5，即b的位置。
id：mx所对应的回文中心。
p[i]：以i为中心的回文串向某一边最多延伸的长度。同样是上面那个例子，p[3]=3,p[7]=2,p[1]=1.

然后直接上代码：

for (int i=1;i<=n;++i)
{
    if (mx>i) p[i]=min(p[2*id-i],mx-i);
    else p[i]=1;
    while (s[i-p[i]]==s[i+p[i]]) ++p[i];
    if (i+p[i]>mx)
    {
        mx=i+p[i];
        id=i;
    }
}

这样，我们就求出来了p[i]。
网上有很多关于manacher算法时间复杂度的证明，我感觉很奇怪，由于mx的单调性，感受一下时间复杂度显然是$O(n)$的。

整个算法的关键是通过i关于id的对称点的回文串来更新i的回文串。贴上几个图来看正确性显然。

回文自动机

类似AC自动机的一种回文串匹配自动机，也就是一棵字符树。准确的说，是两颗字符树，0号表示回文串长度为偶数的树，1号表示回文串长度为奇数的树。每一个节点都代表一个字符串，并且类似AC自动机那样，有字符基个儿子，它的第i个儿子就表示将字符基的第i个字符接到它表示的字符串两边形成的字符串。
同样类似AC自动机的是，每一个节点都有一个fail指针，fail指针指向的点表示当前串后缀中的最长回文串。特殊地，0号点的fail指针指向1，非0、1号点并且后缀中不存在回文串的节点不指向它本身，而是指向0.

变量声明：
len[i]：编号为i的节点表示的回文串的长度（一个节点表示一个回文串）。
ch[i][c]：编号为i的节点表示的回文串在两边添加字符c以后变成的回文串的编号（儿子）。
fail[i]：节点i失配以后跳转不等于自身的节点i表示的回文串的最长后缀回文串。
cnt[i]：节点i表示的本质不同的串的个数（建树时求出的不是完全的，最后重新统计一遍以后才是正确的）。
last：新添加一个字母后所形成的最长回文串表示的节点。
s[i]：第i次添加的字符（一开始设S[0] = -1，也可以是任意一个在串S中不会出现的字符）。
tot：添加的节点个数。
n：添加的字符个数。

下面是一个字符串abbaabba的回文自动机的建立过程。

















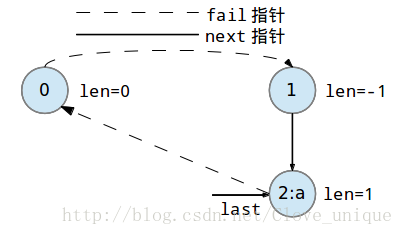
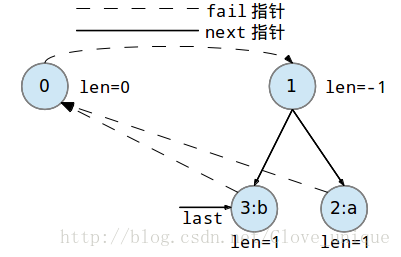
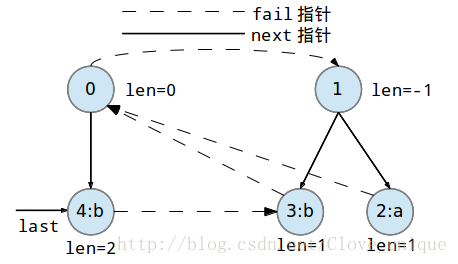
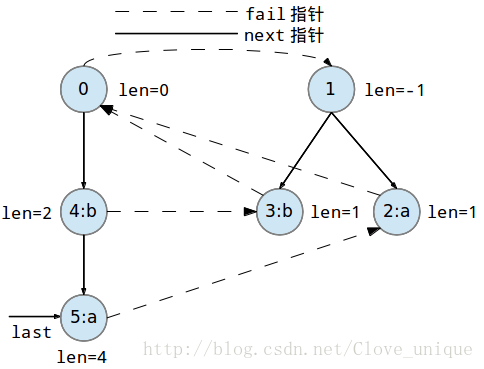
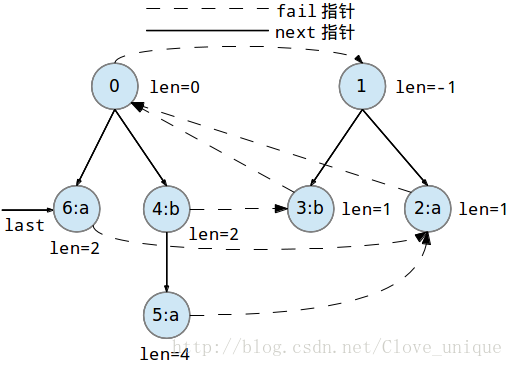
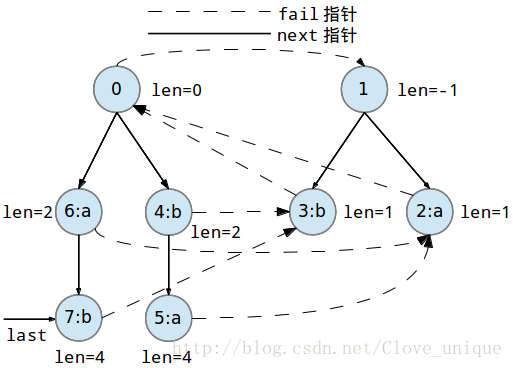
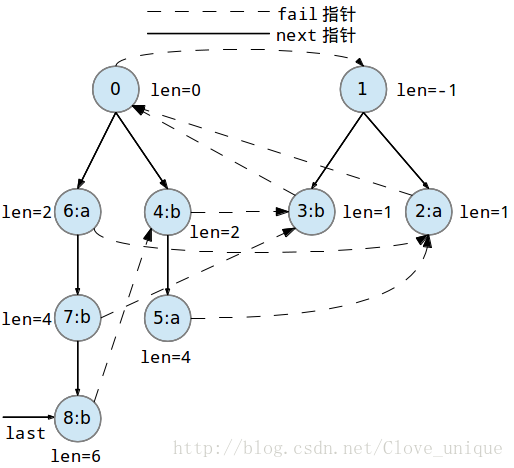
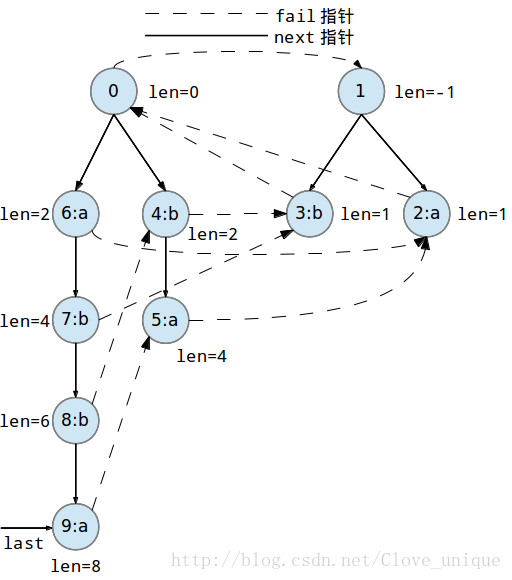
这个建树的过程看起来比较抽象，实际上，回文自动机的实质就是按顺序添加字符，每添加一个字符都要找出以这个字符为后缀的最长的回文串，方法就是在以前一个为后缀的所有回文串中找到一个可以和这个点匹配的，然后再加入到树中。
注意区分一下“字符”和“节点”的概念，一个字符就是字符串中的一个字符，而回文自动机当中的节点表示了一个字符串。

#include<algorithm>
#include<iostream>
#include<cstring>
#include<cstdio>
#define N 300010
#define LL long long
char s[N];
int n,now,cur,fail[N],cnt[N],len[N],tot,last,ch[N][26];
LL ans;

int newnode(int x)
{
    len[tot]=x;
    return tot++;
}
int get_fail(int x,int n)
{
    while(s[n-len[x]-1]!=s[n]) x=fail[x];
    return x;
}
LL Max(LL a,LL b)
{
    return (a>b)?a:b;
}
int main(){
    gets(s+1);
    s[0]=-1;fail[0]=1;last=0;
    newnode(0);newnode(-1);
    for(n=1;s[n];++n)
    {
        s[n]-='a';
        cur=get_fail(last,n);
        if (!ch[cur][s[n]])
        {
            now=newnode(len[cur]+2);
            fail[now]=ch[get_fail(fail[cur],n)][s[n]];
            ch[cur][s[n]]=now;
        }
        cnt[last=ch[cur][s[n]]]++;
    }
    for(int i=tot-1;i>=0;--i)
        cnt[fail[i]]+=cnt[i],ans=Max(ans,(LL)cnt[i]*(LL)len[i]);
    printf("%lld\n",ans);
}