杨氏矩阵/杨图x杨表（知识点总结）

Code92007

已于 2023-10-07 13:59:33 修改

阅读量622

点赞数

分类专栏：知识点总结文章标签：矩阵线性代数杨表杨图

于 2023-10-07 13:53:55 首次发布

本文链接：https://blog.csdn.net/Code92007/article/details/133254118

版权

知识点总结专栏收录该内容

89 篇文章 6 订阅

订阅专栏

思路来源

https://www.cnblogs.com/henrici3106/p/16710990.html

1 到 N 的排列，最长上升子序列（LIS）长度的期望是多少？ - 知乎

杨氏矩阵 - OI Wiki

心得

感觉可能有用的就是一个Hook公式（勾长公式）吧

以及之前有类似的脑补过杨图，现在有了定义更好理解

以下图片，均来自于oiwiki

杨图（Ferrers图）

定义：整数划分中，表示一种具体的划分方案的图

比如对于10=5+4+1，(5,4,1)有如下杨图，英式递减，法式递增

英式：

法式：

杨表

杨表定义

对于n的一个整数拆分 $\lambda$ ，满足 $\lambda = (\lambda_{1},\lambda_{2},...,.\lambda_{m}),\sum_{i=1}^{m}\lambda_{i}=n,\lambda_{i}\geqslant \lambda_{i+1}$ ，记作 $\lambda \vdash n$ 。

标准杨表

将长为n的排列填入杨图，满足每行每列元素单调递增的方案。

半标准杨表

将数字填入杨图，满足每行单调不降、每列单调递增的方案。

RSK算法

边角

一个格子 (s, t) 是边角当且仅当 (s + 1, t) 和 (s, t + 1) 都不存在格子。

插入

1. 在当前行中找到最小的比 x 大的数 y。

2. 如果找到了，交换x和y，去下一行，用换下来的数继续执行操作1。

3. 如果找不到，就把 x 放在该行末尾并退出。此时记 x 在第 s 行第 t 列，则(s, t) 必定是一个边角。

删除

1. 只删除边角(x,y)，可以看做是插入操作的逆操作。

2. 删除一个处于第i行的x时，

①如果i=1，直接退出；

②否则，找到上一行最大的小于x的数y，交换x、y，并移步到上一行，继续考虑

一些性质

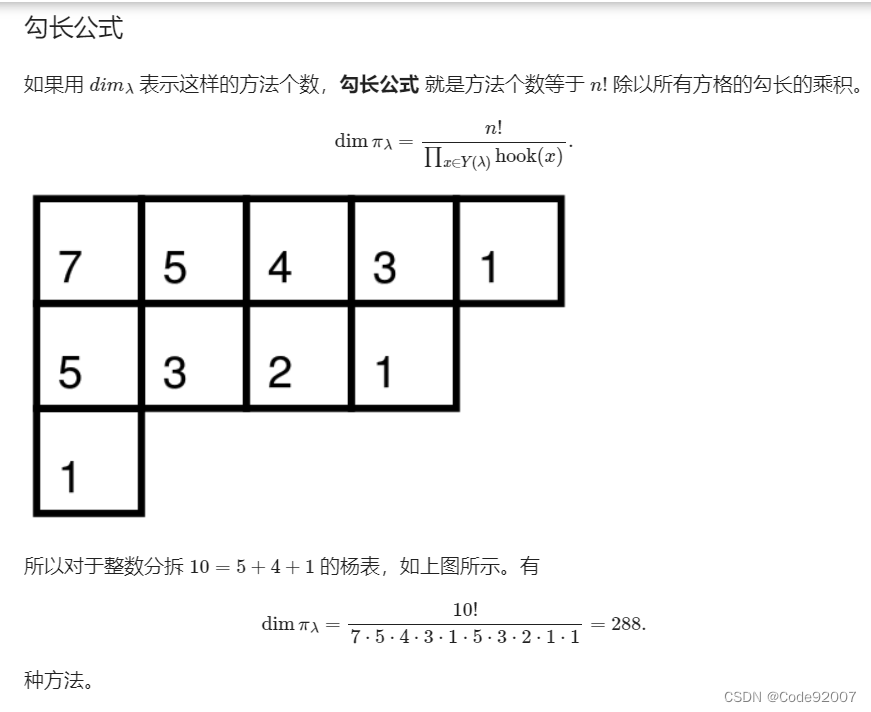
Hook公式

n个方格的杨表填n的排列，使得每一列从上到下递减，每一行从左到右递减，求总方案数

定义每个方格的勾长=同行右边的方格数+同列下面的方格数+1

即： $dim_{\pi_{\lambda}}=\frac{n!}{\prod_{x\epsilon Y(\lambda)hook(x)}}$

记录表

对于排列 $p_{i}$ 而言，设当前插入位置为 (x,y)

定义 P为 pi 顺序插入得到的杨表，

Q 为在 (x,y) 插入对应下标 i 得到的杨表，称为记录表，

并维持 Q 和 P 的形状相同。

例如：

$p_{i} = [1,5,3,2,6,7,4], P=\begin{bmatrix} 1 & 2 & 4 & 7\\ 3 & 6 & & \\ 5 & & & \end{bmatrix}, Q= \begin{bmatrix} 1 & 2 & 5 & 6\\ 3 & 7 & & \\ 4 & & & \end{bmatrix}$

Robinson-Schensted correspondence

一个 1 到 n 的排列 pi 与一对形状相同的标准杨表形成双射。

也就是说，设 $f_{\lambda}$ 为形状为 $\lambda$ 的填数方案，有： $\sum_{\lambda \vdash n} {f_{\lambda }^2} = n!$ 成立

证明：

充分性：对于一个排列 $p_{i}$ ，有唯一对应的一对P、Q。

必要性：给定杨表P、Q，通过在P中不断删去Q中最大的元素（ $p_{i}$ 的最后一个元素），能唯一对应一个排列。

拆分数p(n)

记n的拆分数为p(n)，则下式可以估算其量级： $p(n)\sim \frac{1}{4n\sqrt3}exp(\pi \sqrt\frac{2n}{3})$

LIS/LDS长度

杨表的第一行就是序列的LIS/LDS（最长上升子序列/最长下降子序列）的长度，记为 $\lambda_{1}$

例题

BJWC2018 最长上升子序列

题意

求长为n(n<=28)的排列的最长上升子序列长度的期望

思路来源

EI的讲解：题解 P4484 【[BJWC2018]最长上升子序列】 - Elegia - 洛谷博客

题解

这题用状压dp不太好做，用杨表就是暴力枚举整数拆分+公式统计了

注意到拆分数的量级，所以，可以直接暴力枚举每个整数划分，

利用hook公式，求每个形状的杨表数量，

借助Robinson-Schensted correspondence帮助还原排列，

每个杨表的贡献是 $\lambda_{1}$ ，统计答案

代码

#include<bits/stdc++.h>
using namespace std;
#define rep(i,a,b) for(int i=(a);i<=(b);++i)
#define per(i,a,b) for(int i=(a);i>=(b);--i)
typedef long long ll;
typedef double db;
typedef pair<int,int> P;
#define fi first
#define se second
#define dbg(x) cerr<<(#x)<<":"<<x<<" ";
#define dbg2(x) cerr<<(#x)<<":"<<x<<endl;
#define SZ(a) (int)(a.size())
#define sci(a) scanf("%d",&(a))
#define pb push_back
#define pt(a) printf("%d",a);
#define pte(a) printf("%d\n",a)
#define ptlle(a) printf("%lld\n",a)
#define debug(...) fprintf(stderr, __VA_ARGS__)
std::mt19937_64 gen(std::chrono::system_clock::now().time_since_epoch().count());
ll get(ll l, ll r) { std::uniform_int_distribution<ll> dist(l, r); return dist(gen); }
const int N=30,mod=998244353;
int n,inv[N],a[N],ans;
void dfs(int x,int y){
	if(!x){
		int res=1;
		rep(i,1,n){
			res=1ll*res*i%mod;
		}
		rep(i,1,y-1){
			rep(j,1,a[i]){
				int ct=a[i]-j;
				rep(k,i,y-1){
					if(a[k]>=j)++ct;
				}
				res=1ll*res*inv[ct]%mod;
			}
		}
		ans=(ans+1ll*res*res%mod*a[1]%mod)%mod;
	}
	rep(i,1,x){
		if(y!=1 && i>a[y-1])continue;
		a[y]=i;
		dfs(x-i,y+1);
	}
}
int main(){
	sci(n);
	inv[1]=1;
	rep(i,2,n){
		inv[i]=1ll*(mod-mod/i)*inv[mod%i]%mod;
	}
	dfs(n,1);
	rep(i,1,n){
		ans=1ll*ans*inv[i]%mod;
	}
	printf("%d\n",ans);
	return 0;
}