插入排序和希尔排序

最新推荐文章于 2025-04-24 22:38:22 发布

知困勉行的Allen

最新推荐文章于 2025-04-24 22:38:22 发布

阅读量1.1k

点赞数 17

文章标签：排序算法算法数据结构学习方法 c语言 c++

本文链接：https://blog.csdn.net/Code_Allen/article/details/147335626

版权

今天给小伙伴们分享两个比较基础的排序算法，插入排序和希尔排序，这两个排序算法之间联系还是挺多的，所以放在一起。希尔排序可以看作是插入排序的升级版，在面对一些更为复杂的场景时，希尔排序的效率往往要比插入排序高的多。那咱们先介绍吧~

插入排序

插入排序（Insertion Sort）是一种简单直观的排序算法，它的工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。插入排序在实现上，通常采用in-place排序（即只需用到O(1)的额外空间的排序），因而在从后向前扫描过程中，需要反复把已排序元素逐步向后挪位，为最新元素提供插入空间。核心思想是将未排序部分的元素逐个插入到已排序部分的正确位置。类似于整理扑克牌时的排序方式。

实际运作场景类似下面动图

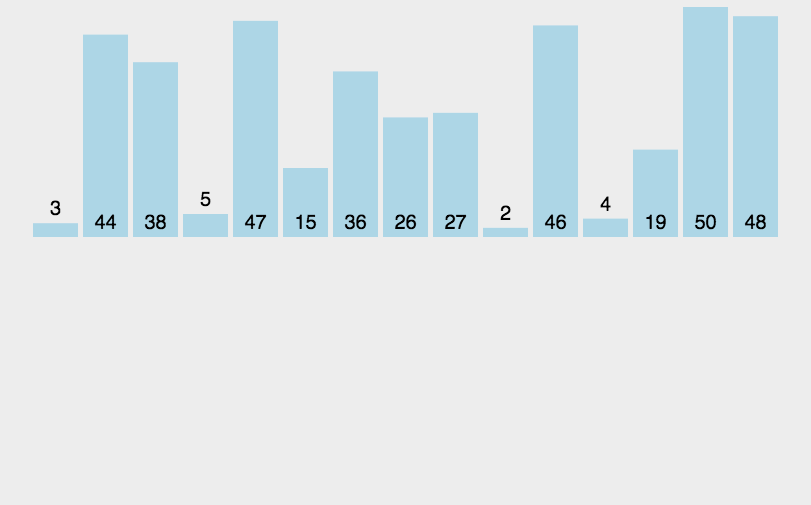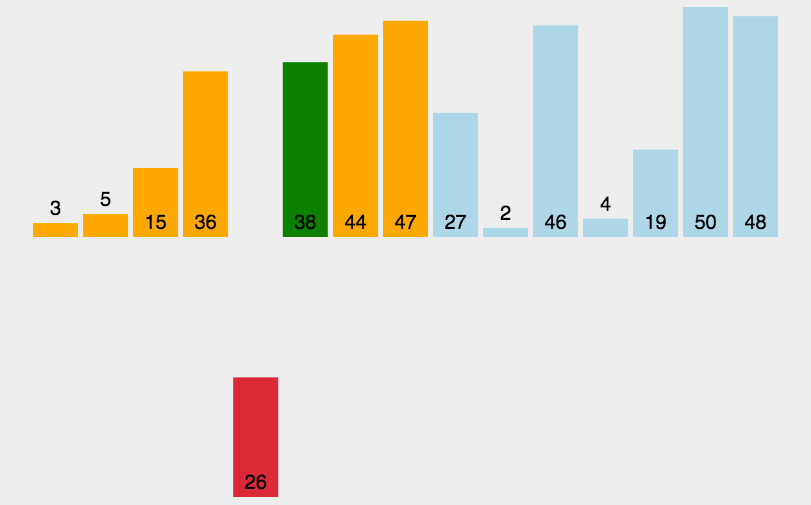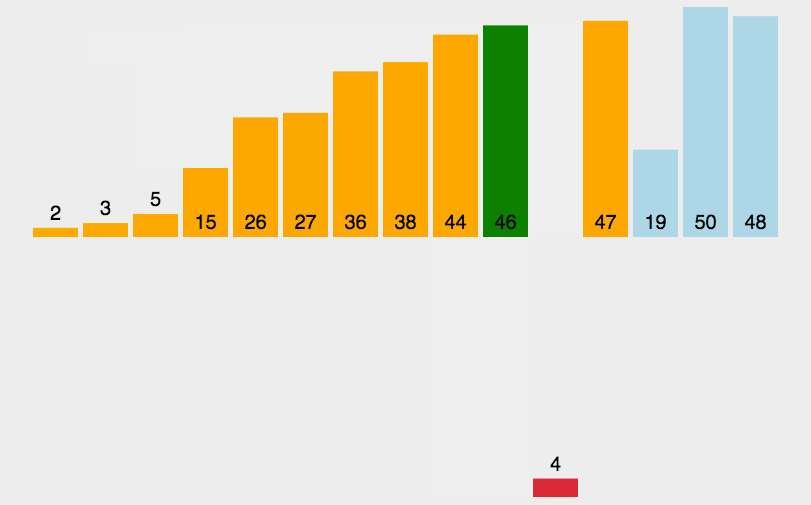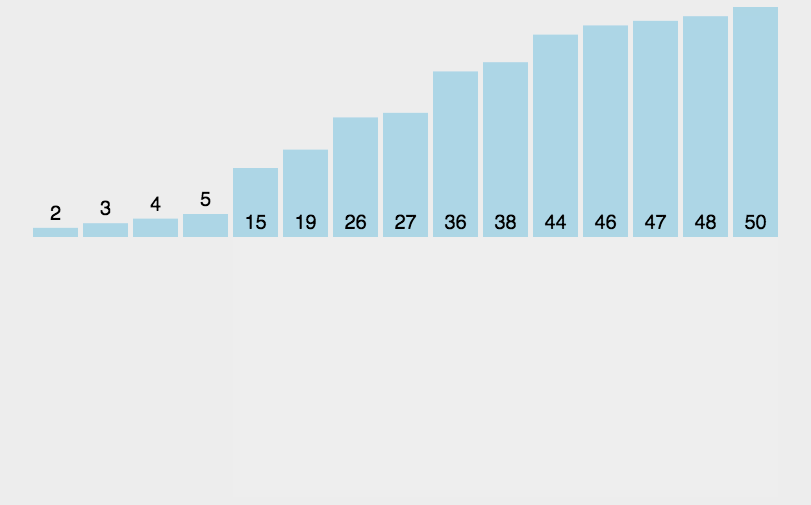
算法步骤

初始状态：
- 将数组第一个元素视为已排序部分
- 其余元素为未排序部分
排序过程：
- 从未排序部分取出第一个元素
- 在已排序部分从后向前扫描
- 找到合适位置插入该元素
- 重复直到所有元素排序完成
终止条件：
- 未排序部分为空

算法特点

时间复杂度：
- 最优情况（已排序数组）：O(n)
- 最差情况（逆序数组）：O(n²)
- 平均情况：O(n²)
空间复杂度：
- O(1)（原地排序）
稳定性：
- 稳定排序（相等元素的相对位置不变）
适用场景：
- 小规模数据排序
- 基本有序的数据
- 作为其他高级算法（如快速排序）的子过程


#include <stdio.h>

void InsertSort(int* a, int n)
{
	for (int i = 1; i < n; i++)
	{
		int end = i - 1;
		int tmp = a[i];
		// 将tmp插入到[0,end]区间中，保持有序
		while (end >= 0)
		{
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
				--end;
			}
			else
			{
				break;
			}
		}

		a[end + 1] = tmp;
	}
}




int main()
{
    int arr[] = { 12, 11, 13, 5, 6 };
    int n = sizeof(arr) / sizeof(arr[0]);

    printf("排序前: ");
    for (int i = 0; i < n; i++) printf("%d ", arr[i]);
	InsertSort(arr, n);

    printf("\n排序后: ");
    for (int i = 0; i < n; i++) printf("%d ", arr[i]);

    return 0;
}

总结

插入排序以其实现简单和对小规模数据的高效性著称，虽然在大数据量时性能较差，但仍然是许多复杂排序算法（如TimSort）的基础组成部分。理解其原理有助于掌握更高级的排序技术。

希尔排序

希尔排序（Shell Sort）是一种基于插入排序的算法，由D.L. Shell在1959年提出。它通过比较距离一定间隔的元素来工作，然后逐步减小间隔来排序元素。希尔排序的效率比传统的插入排序要高，因为它利用了数组元素之间的“已排序”关系，从而减少必要的比较和移动次数。

算法原理

希尔排序的基本思想是将整个待排序的记录序列分割成为若干子序列分别进行直接插入排序，从而使得整个序列基本有序，最后再对全体记录进行一次直接插入排序。这种方法也被称为“缩小增量排序”。

算法步骤

选择一个增量序列 g，例如 g={n/2,n/4,...,1}，其中 n 是数组的长度。
对于增量序列中的每个增量 gi，执行以下操作：
- 从第 gi 个元素开始，对每隔 gi 个元素进行直接插入排序。
当增量序列为空时，排序完成。

算法特点

其实希尔排序对比插入排序，就是多了一个预排序的过程，这个预排序的过程不要求彻底排好，通过不断减小排序间隔，使得排序更加高效。当间隔为 1 时，希尔排序的过程就是插入排序。

1 .时间复杂度：

希尔排序的时间复杂度取决于增量序列的选择：

最坏情况：O(n²)（使用某些增量序列时）
最好情况：O(n log n)
平均情况：根据增量序列不同而变化，常见为O(n^(3/2))

2 .空间复杂度：

O(1) - 原地排序算法

3.稳定性：

不稳定 - 相同元素可能在分组排序过程中改变相对位置

4.适用场景：

希尔排序适用于中等规模的数据排序，特别是当数据部分有序时表现较好。

#include <stdio.h>

void shellSort(int arr[], int n) 
{
    // 初始增量gap为数组长度的一半，然后逐步缩小
    for (int gap = n / 2; gap > 0; gap /= 2) 
    {
        // 从gap位置开始，对各个子序列进行插入排序
        for (int i = gap; i < n; i++)
        {
            int temp = arr[i];
            int j;
            // 对子序列进行插入排序
            for (j = i; j >= gap && arr[j - gap] > temp; j -= gap) 
            {
                arr[j] = arr[j - gap];
            }
            arr[j] = temp;
        }
    }
}

// 打印数组的函数
void printArray(int arr[], int size) 
{
    for (int i = 0; i < size; i++) 
    {
        printf("%d ", arr[i]);
    }
    printf("\n");
}

int main() 
{
    int arr[] = { 12, 25, 58, 99, 36, 2, 9, 88, 7 };
    int n = sizeof(arr) / sizeof(arr[0]);

    printf("排序前的数组: \n");
    printArray(arr, n);

    shellSort(arr, n);

    printf("排序后的数组: \n");
    printArray(arr, n);

    return 0;
}