理解数学概念——同伦和简单连通域

ComputerInBook

已于 2024-12-04 10:45:23 修改

阅读量1.5k

点赞数 16

分类专栏：数学与应用数学文章标签：同伦拓扑学单连通简单连通连通域

于 2024-03-16 16:16:29 首次发布

本文链接：https://blog.csdn.net/ComputerInBook/article/details/136764322

版权

数学与应用数学专栏收录该内容

130 篇文章

订阅专栏

1. 同伦(homotopy)

1.1 homotopy[hɒməʊˈtɒpi] n.

(1) <<The Oxford English Dictionary>>第二版：

[数学专用术语，这个词由德语homotopie改造而来，(Dehn & Heegaard Analysis Situs in Encykl.d.math.Wiss.(1907) III.I.I.164页)：see prec. and $-\rm{Y}^{3}$ . ]

a. A mapping that deforms one path continuously into another in such a way that all the intermediate paths lie within the topological space of which the two given paths are subspaces(see quot. 1970).

这是一种映射，已知两条路径，它将其中一条路径经过连续变形(改变其外形)变为另一条路径，使得所有中间路径都位于拓扑空间内，其中两个给定路径是该拓扑空间的子空间(参见引用1970)。

b. The property of being homotopic.

作为同伦的属性本身。

(2) 词源构成

homotopy 由“homo-”+ “-topy”构成：

“homo-”的词义为“same, the same, equal, like(同，相同，相等，相似)”；

“-topy”的词义为“location,position(位置)”，是一个名词构词后缀，来自新拉丁语“-topia”(来自希腊语)，词义为“way,place(方式，位置)”，由“topos”(词义为“place(位置，地点)”) + “-ia,-y”构成。

而在汉语中，“倫(伦)”的本意是“辈；同类”。所以，“同伦”应理解为“具有相同的某种属性”的意思，同伦这个汉语只体现了这个数学概念的一半意义，另一半意义并没有体现出来。

1.2 homotopic[hɒməʊˈtɒpik] adj.

名词homotopy对应的形容词。

1.3 同伦的数学解释

在拓扑学中(topology,研究“位置、空间、区域”的学问)，对于两个连续函数，如果其中一个可以在一个拓扑空间经过连续变换变形为另一个拓扑空间中的另一个函数，则称这两个拓扑空间是同伦的(homotopic,来自古希腊词“ὁμός homós”(词义为“same, similar (相同，类似)”和“τόπος tópos”(词义为“place(地位，位置)”))。而这种变形的行为，称为两个函数之间的同伦(homotopy)。同伦的一个显著用途是用于定义同伦群(homotopy groups)和上同伦群(cohomotopy groups)——代数拓扑中的重要不变量。

令 $\gamma_{0}$ 和 $\gamma_{1}$ 为开集Ω 中的两条具有相同端点的曲线。因此，若 $\gamma_{0}(t)$ 和 $\gamma_{1}(t)$ 是两个定义于[a,b] 上的参数化表达式，则我们有

$\gamma_{0}(a) = \gamma_{1}(a) = \alpha$ 和 $\gamma_{0}(b) = \gamma_{1}(b) = \beta$ 。

若对于每一个 0 ≤ s ≤ 1 ，存在一条曲线 $\gamma_{s} \subset \Omega$ ，可以用定义于 [a,b] 上的 $\gamma_s(t)$ 参数化，使得对每一个 s ，有

$\gamma_s(a) = \alpha$ 和 $\gamma_s(b) = \beta$ ，

以及对于任意 t∈[a,b],有

$\gamma_{s}(t)\left . \right |_{s=0} = \gamma_{0}(t)$ 和 $\gamma_{s}(t)\left . \right |_{s=1} = \gamma_{1}(t)$ ,

则称这两条曲线在 Ω 中是同伦的(homotopic)。此外， $\gamma_{s}(t)$ 在 s∈[0,1] 和 t∈[a,b] 中应当是联合连续的。

大致地讲，对于两条曲线，若其中一条曲线可以通过连续变换变形为另一条曲线而不离开Ω，则这两条曲线是同伦的(如图1所示)。

---------------------------------------------------图1. 曲线的同伦---------------------------------------------

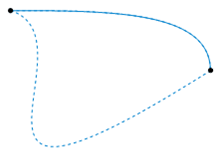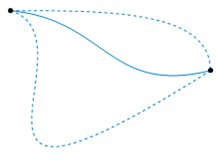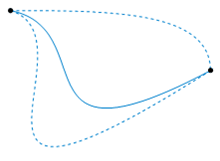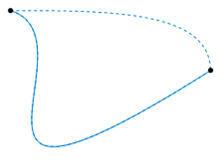
---------------------------------------------------图2. 上面显示的两条虚线路径相对于它们的端点是同伦的。该动画代表一种可能的同伦。-----------------------------------------------------------------------------

---------------------------------------------------图3. $R^{3}$ 中环面的两个嵌入之间的同伦：作为“甜甜圈的表面”和“咖啡杯的表面”。这也是同位素的一个例子。---------------------------------------------------------

2. 简单连通域(simply connected region)(一个拓扑学概念)

如果复平面上的一个区域内的任何简单闭合曲线(译注：除了端点处重合，闭合曲线的其它部分不相交)可以连续变形为一点而不离开该区域，则该区域是简单连接的。这意味着该区域中没有任何“洞(holes)”或“把手(handles)”，因为曲线始终可以收缩到一个点而不跨越边界。这是该定义的直观含义，可以通过想象一根绳子在该区域内收缩来形象化。连续变形的过程称为同伦，并由参数化曲线与点或另一条曲线之间可能的循环的函数表示。这个概念也可以使用基本群来描述，但它更高级。而单纯一个连通域可以有多个组成部分或者孔。简单连通域有边界，边界是简单连通域的一部分。

简单连通区域在许多数学领域都很重要，包括拓扑、复分析和微分几何。它们提供了一种对不同类型的空间进行分类和研究的方法，并可以帮助解决与这些领域相关的问题。

有几种不同的方法可以确定一个区域是否是简单连接的。一种方法是检查是否有任何循环可以连续收缩到单个点而不离开该区域。另一种方法是使用代数拓扑，其中涉及查看该区域的基本群。如果基本群是平凡的（意味着它只包含单位元素），则该区域是单连通的。例如，下面的方法：

对于复平面上的区域Ω ，若Ω 中任意两条具有相同端点的成对曲线是同伦的，则此区域Ω是简单连通的(simply connected)。