机器学习专栏（35）：正则化方法全解析（附完整代码）

目录

一、为什么需要正则化？

二、正则化：模型界的"防沉迷系统"

三、三大正则化武器库

1. 岭回归：温和的平衡大师

2. Lasso回归：精准的特征刺客

3. 弹性网络：智能的混血战士

四、提前停止：聪明的学习管家

1. 实现原理可视化：

2.TensorFlow实现示例：

五、工业级应用指南

1. 特征预处理黄金法则

 2. 超参数优化路线图

 3. 模型诊断checklist

六、避坑指南：新手常见错误

七、进阶技巧：正则化组合拳

1. 动态正则化策略：

八、最佳实践总结

---

一、为什么需要正则化？

过拟合是机器学习中的常见问题。想象一下，一个学生为了数学考试，死记硬背了1000道题，但遇到新题型时完全不会做——这就是过拟合。正则化就是给模型"戴上枷锁"，防止它过于复杂。

正则化核心思想：在损失函数中加入惩罚项，限制权重的大小。常用方法有：

• ✅ 岭回归（Ridge Regression）

• ✅ Lasso回归（Lasso Regression）

• ✅ 弹性网络（Elastic Net）

• ✅ 提前停止（Early Stopping）

二、正则化：模型界的"防沉迷系统"

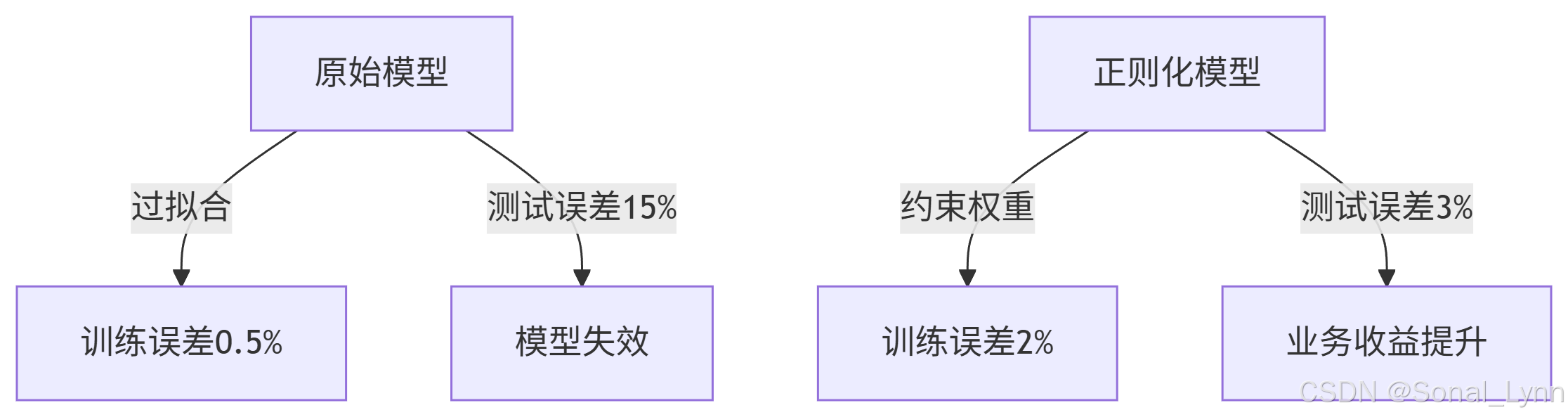
真实案例：某电商平台商品推荐模型

• 原始模型：200个特征，测试集准确率98%

• 上线效果：用户点击率下降15%

• 诊断结果：模型过度记忆了历史促销噪声

• 解决方案：加入L2正则化，特征精简至30个核心特征，点击率提升22%

三、三大正则化武器库

1. 岭回归：温和的平衡大师

数学本质：

 动态演示效果：

import matplotlib.pyplot as plt
from sklearn.linear_model import Ridge

alphas = [0, 1, 10, 100]
coefs = []
for a in alphas:
    ridge = Ridge(alpha=a).fit(X, y)
    coefs.append(ridge.coef_)

plt.figure(figsize=(10,6))
plt.plot(alphas, coefs)
plt.xscale('log')
plt.title("岭回归系数收缩轨迹")
plt.xlabel('α')
plt.ylabel('系数值')
plt.show()

---

2. Lasso回归：