题意:
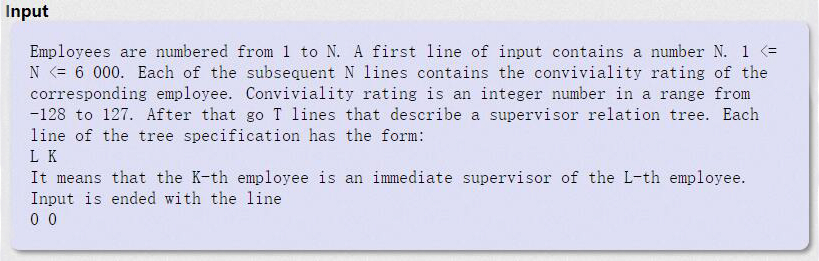
给一个n,代表有n个人,接下里n行给出一个第i个人的欢乐值,再接下来n-1行给出两两之间的关系(有直接联系,就是表示一个是上司一个是下属)。要求不能跟其有直接联系的人参加这个聚会(上司跟下属不能同时参加这个聚会),问这个聚会最大的欢乐值是多少。
题解:
树形DP的入门题。
状态为两维 dp[i][j] 第一维表示当前子树的根节点,第二维表示去还是不是 0代表不去,1代表去。
输入的时候,每个人的欢乐值可直接为dp[i][1]代表他们去的时候的欢乐值。
因为题目没有给根节点的下标,记得在输入完之后,找到根节点,从根节点开始往下遍历。
那么转移的时候,只有两种情况
① 上司不去,那么看该下属去的时候的值比较大,还是不去的时候比较大。
dp[now][0]+=max(dp[next][0],dp[next][1])
②上司去,那么下属就不能去。
dp[now][1]+=dp[next][0]
#pragma comment(linker, "/STACK:102400000,102400000")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<algorithm>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<vector>
using namespace std;
typedef long long ll;
const int N=6e3+5;
int dp[N][2];//0不去 1去
int fa[N];
vector<int>vc[N];
int n;
void dfs(int root)
{
for (int i=0 ; i<vc[root].size() ; ++i)
{
int next=vc[root][i];
dfs(next);
dp[root][1]+=dp[next][0];//上司去了 所以员工不能去
dp[root][0]+=max(dp[next][0],dp[next][1]);//上司不许,员工可以选择去或不去
}
}
int main()
{
while (~scanf("%d",&n))
{
memset(fa,0,sizeof(fa));
memset(dp,0,sizeof(dp));
for (int i=1 ; i<=n ; ++i)
vc[i].clear();
for (int i=1 ; i<=n ; ++i)
scanf("%d",&dp[i][1]);
int L,K;
int root=1;
while (~scanf("%d%d",&L,&K) && (L+K))
{
fa[L]=K;
vc[K].push_back(L);
root=K;
}
while (fa[root])
root=fa[root];
dfs(root);
printf("%d\n",max(dp[root][0],dp[root][1]));
}
return 0;
}






























 378
378

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








