题意:
给T组数据,每组数据含有 L,R,l,r, 求出函数
其中f(i,j)表示
题解:
这很容易把思维转向知道R里面有多少个回文数,L-1(因为范围包括了L)里面有多少个回文数,减去差值然后乘上权值j,,再加上[L,R]之间不能构成回文数的个数,就可以得到答案了。
其中,十进制的回文数判断,在LightOJ1205出现过,如果没做过的,可以现去做做这题。
我们用同样的方法,只要多一维记录下当前进制。
那么最后我们可以得到dp[k][i][j][2] 第一维表示k进制下,第二维表示当前位置,第三维表示回文数的长度(从0开始,理解为起点也可以),第四维表示是否能构成回文串。
每次记录下当前枚举的数。
判断过程中,对前导0作处理,也就是说当当前位置与回文数长度一致时,而当前枚举为0,那么回文数长度跟着当前位置减一,然后再继续往下找。
当当前位置距离回文数的长度,超过了一半的时候,开始判断后面枚举的数是否与前面已经枚举了的数出现回文。
最后根据f(i,j)的值,对回文数的个数处理一下就好。
T_T 一开始我还傻傻的以为自己算错算错,其实只是算了回文数的个数。
#pragma comment(linker, "/STACK:102400000,102400000")
#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#include<string>
#include<algorithm>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<vector>
using namespace std;
typedef long long ll;
const int M=40;
ll dp[M][M][M][2];
int num[M],tmp[M];
ll dfs(int pos,int k,int cnt,bool state,bool limit)
{
if (pos==-1)
return state;
if (!limit && dp[k][pos][cnt][state]!=-1)
return dp[k][pos][cnt][state];
int up=limit?num[pos]:k-1;
ll res=0;
for (int i=0 ; i<=up ; ++i)
{
tmp[pos]=i;
if (pos==cnt && !i)
res+=dfs(pos-1,k,cnt-1,state,limit && i==num[pos]);
else if (state && pos<(cnt+1)/2)
res+=dfs(pos-1,k,cnt,i==tmp[cnt-pos],limit && i==num[pos]);
else
res+=dfs(pos-1,k,cnt,state,limit && i==num[pos]);
}
if (!limit)
dp[k][pos][cnt][state]=res;
return res;
}
ll solve(int x,int k)
{
int pos=0;
while (x)
{
num[pos++]=x%k;
x/=k;
}
ll ans=dfs(pos-1,k,pos-1,1,1);
return ans;
}
int main()
{
memset(dp,-1,sizeof(dp));
int T;
scanf("%d",&T);
for (int test=1 ; test<=T ; ++test)
{
int L,R,l,r;
scanf("%d%d%d%d",&L,&R,&l,&r);
ll ans=0;
for (int i=l ; i<=r ; ++i)
{
ll rn=solve(R,i);
ll ln=solve(L-1,i);
ans+=(rn-ln)*i;
ans+=(R-rn-(L-1-ln));
}
printf("Case #%d: %lld\n",test,ans);
}
return 0;
}







 本文介绍了一种解决特定回文数求和问题的高效算法。该算法通过动态规划预先计算不同进制下指定范围内回文数的数量,并考虑了边界情况如前导零等细节。最终实现了快速求解给定区间内所有回文数及其数量。
本文介绍了一种解决特定回文数求和问题的高效算法。该算法通过动态规划预先计算不同进制下指定范围内回文数的数量,并考虑了边界情况如前导零等细节。最终实现了快速求解给定区间内所有回文数及其数量。





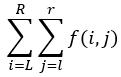

















 9292
9292

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








