数学-素数筛及其拓展

以前写筛法都这么写:

埃拉托斯尼斯筛法

void getprime(int n)
{
	for(int i=2;i<=n;i++)
	if(!v[i])
	{
		prime[ptot++]=v[i];
		for(int j=i<<1;j<=n;j+=i)
		v[j]=true;
	}
}

复杂度O(nlglgn).

实测n=1kW耗时0.18s ; n=1E耗时2.24s.

然后这里是欧拉线性筛

void getprime(int n)
{
	for(int i=2;i<=n;i++)
	{
		if(!v[i]) prime[ptot++]=i;
		int k;
		for(int j=0;j<ptot && ((k=i*prime[j])<=n);j++)
		{	
			v[k]=true;
			if(i%prime[j]==0) break;
		}
	}
}

复杂度O(n).

实测n=1kW耗时0.1s,n=1E耗时1.02s.

看得出,尽管有乘除操作,但是线性筛在十万以上的n,速度就已经超越了普通筛法.

所以在n<=20W的范围上可以直接用埃拉托斯尼斯筛法,更大的话就用线性筛加速.

证明大概是说明两点,一是所有合数都被标记了,二是所有数最多被标记一次.证明就不多说了.....

然后,就是素数筛求积性函数.用这个做法是因为线性筛把所有数的最小素因子求出来了.

比如求莫比乌斯函数....

void getmou(int n)
{
	mou[1]=1;
	for(int i=2;i<=n;i++)
	{
		if(!v[i]) prime[ptot++]=i,mou[i]=-1;
		int k;
		for(int j=0;j<ptot && ((k=i*prime[j])<=n);j++)
		{	
			v[k]=true;
			mou[k]=-mou[i];
			if(i%prime[j]==0)
			{
				mou[k]=0;
				break;
			}
		}
	}
}

大概意思是,这样的:

首先素数的函数值就是-1.

然后,我们在筛合数的时候,是i*prime[j]的形式,而prime[j]是i*prime[j]的最小素因子.

如果这个合数不存在平方因子,那么根据莫比乌斯函数的定义,mou[i*prime[j]]=-mou[i];

如果这个合数存在平方因子,那么 mou[i*prime[j]]=0;

至于直接写mou[k]=-mou[i],是因为如果

1.i本身就有平方因子了,那么明显mou[i]=0,于是mou[k]=0=-mou[i];

2.i在乘上prime[j]后才出现平方因子,这说明prime[j]是平方因子,prime[j]整除i,

所以要对prime[j]整除i的情况特判,让mou[i*prime[j]]=0.

线性筛还能快速求欧拉函数表.

void geteular(int n)
{
	eu[1]=1;
	for(int i=2;i<=n;i++)
	{
		if(!v[i]) prime[ptot++]=i,eu[i]=i-1;		
		int k;
		for(int j=0;j<ptot && (k=i*prime[j])<=n ; j++)
		{
			v[k]=true;
			eu[k]=eu[i]*(prime[j]-(i%prime[j]!=0));
			if(i%prime[j]==0) break;
		}
	}
}

根据欧拉函数的公式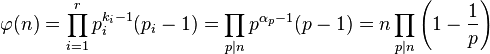(来自wikipedia-CN)可以推出递推式

eu[i*prime[j]]=eu[i]*(prime[j]-(i%prime[j]!=0));

求因数个数函数表(叫做τ(n)或者σ0(n))

void gen(int n)
{
	cnt[1]=fct[1]=1;
	for(int i=2;i<=n;i++)
	{
		if(v[i]==false) prime[ptot++]=i,cnt[i]=2,fct[i]=1;
		int k;
		for(int j=0;j<ptot && (k=i*prime[j])<=n; j++)
		{
			v[k]=true;
			if(i%prime[j]==0)
			{
				fct[k]=fct[i]+1;
				cnt[k]=cnt[i]/(fct[i]+1)*(fct[i]+2);
				break;
			}
			fct[k]=1;
			cnt[k]=cnt[i]*2;
		}
	}
}

为了根据公式(来自度娘百科)计算出它的值,需要额外开一个数组fct存储"i的因数分解中,i的最小质因数有多少次幂".然后根据上边套式子.......

式中求结果的函数也可以写成

cnt[k]=cnt[i]+cnt[i]/(fct[i]+1);