viterbi 算法与python实现

Viterbi算法

（部分内容转自知乎：《如何通俗地讲解 viterbi 算法？》）

1、问题描述

如下如所示，如何快速找到从 S 到 E 的最短路径？

一：遍历穷举法，可行，但速度太慢；

二：viterbi算法！

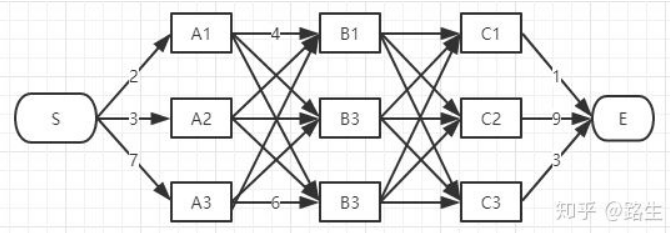
注：viterbi 维特比算法解决的是篱笆型图的最短路径问题，图的节点按列组织，每列的节点数量可以不一样，每一列的节点只能和相邻列的节点相连，不能跨列相连，节点之间有着不同的距离，距离的值就不在图上一一标注出来了，大家自行脑补。

2、算法分析

（1）S 到 A 列的最短路径

首先起点是S，从S到A列的路径有三种可能：S-A1、S-A2、S-A3，如下图：

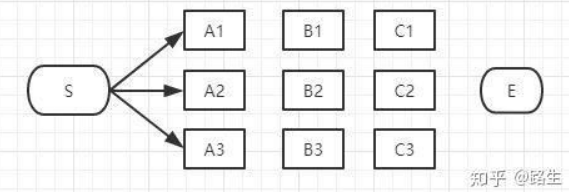
我们不能武断地说S-A1、S-A2、S-A3中的哪一段必定是全局最短路径中的一部分，目前为止任何一段都有可能是全局最短路径的备选项。继续往右看，到了B列，按B列的B1、B2、B3逐个分析。

（2）S 到 B 列的最短路径

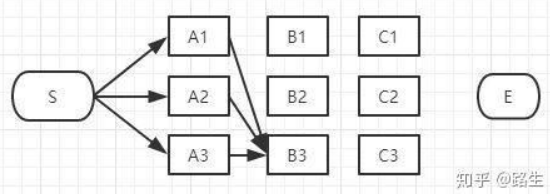
先看 B1，经过B1的所有路径只有3条：S-A1-B1，S-A2-B1，S-A3-B1。

这三条路径，各节点距离加起来对比一下，就可以知道其中哪一条是最短的。假设S-A3-B1是最短的，那么我们就知道了经过B1的所有路径当中S-A3-B1是最短的，其它两条路径路径S-A1-B1和S-A2-B1都比S-A3-B1长，绝对不是目标答案，可以大胆地删掉了。删掉了不可能是答案的路径，就是viterbi算法（维特比算法）的重点，因为后面我们再也不用考虑这些被删掉的路径了。现在经过B1的所有路径只剩一条路径了，如下图：

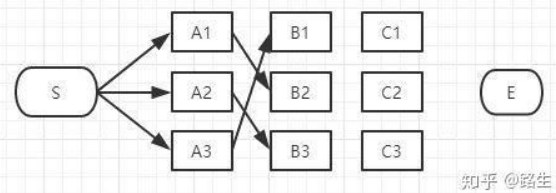
接下来我们继续看B2，同理，经过B2的路径有3条：S-A1-B2，S-A2-B2，S-A3-B2。

这三条路径中，各节点距离加起来对比一下，肯定也可以知道其中哪一条是最短的，其它两条路径路径S-A2-B2和S-A3-B1也可以删掉了。经过B2所有路径只剩一条，如下图：

接下来我们继续看B3，同理，经过B3的路径也有3条：S-A1-B3，S-A2-B3，S-A3-B3。

这三条路径中我们也肯定可以算出其中哪一条是最短的，假设S-A2-B3是最短的，那么我们就知道了经过B3的所有路径当中S-A2-B3是最短的，其它两条路径路径S-A1-B3和S-A3-B3也可以删掉了。经过B3的所有路径只剩一条，如下图：

现在对于B列的所有节点我们都过了一遍，B列的每个节点我们都删除了一些不可能是答案的路径，删掉这些不可能是最短路径的情况之后，留下了三个有可能是最短的路径：S-A3-B1、S-A1-B2、S-A2-B3。现在我们将这三条备选的路径放在一起汇总到下图：

（3）S 到 C 列的最短路径

类似上面说的B列，我们从C1、C2、C3一个个节点分析。

经过C1节点的路径有：S-A3-B1-C1、S-A1-B2-C1、S-A2-B3-C1。

和B列的做法一样，从这三条路径中找到最短的那条（假定是S-A3-B1-C1），其它两条路径同样道理可以删掉了。那么经过C1的所有路径只剩一条，如下图：

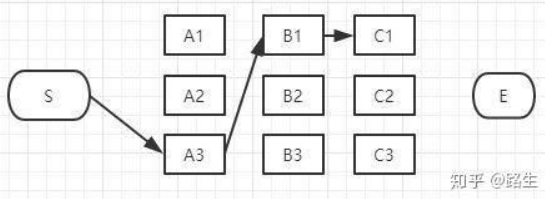
同理，我们可以找到经过C2和C3节点的最短路径，汇总一下：

到达C列时最终也只剩3条备选的最短路径，我们仍然没有足够信息断定哪条才是全局最短。最后，我们继续看E节点，才能得出最后的结论。

（4）S 到 E 的最短路径

到E的路径也只有3种可能性：

E点已经是终点了，我们稍微对比一下这三条路径的总长度就能知道哪条是最短路径了。

在效率方面相对于粗暴地遍历所有路径，viterbi 维特比算法到达每一列的时候都会删除不符合最短路径要求的路径，大大降低时间复杂度。

（以上所有内容转自知乎《如何通俗地讲解 viterbi 算法？》，如有侵权请联系我删除！）

3、python实现

上述问题只涉及节点之间的距离，这里我们假设每个节点本身有一个状态，节点与节点之间的距离用权重表示。为了简化描述和编程方便，将 S 到 A 列的权重全部置为1，C 列到 E 的权重也全部置为1，只考虑A、B、C三列。

用矩阵 state 表示节点的状态，(d, n)=state.shape，d 就表示每一层节点的数量，n 表示总层数。

用矩阵 weight 表示相邻层之间的路径距离，n 层就有 n-1 个权重矩阵，weight[k][i][j] 表示第 k-1 层的节点 i 到第 k 层的节点 j 之间的距离。

import numpy as np

state = [[0.9, 0.1, 0.3],
         [0.1, 0.8, 0.4],
         [0.0, 0.1, 0.3]]
weight = [[[0.1, 0.4, 0.5], [0.2, 0.7, 0.1], [0.9, 0.0, 0.1]],
          [[0.8, 0.1, 0.1], [0.4, 0.3, 0.3], [0.1, 0.2, 0.7]]]


def viterbi(state, weight):
    '''
    :param state: 状态矩阵
    :param weight: 权重矩阵
    :return:
    '''
    state = np.array(state)
    weight = np.array(weight)
    d, n = state.shape
    assert weight.shape == (n - 1, d, d), 'state not match path!'

    # 路径矩阵，元素值表示当前节点从前一层的那一个节点过来是最优的
    path = np.zeros(shape=(d, n))

    for i in range(n):
        print(f'进入第 {i} 层')
        if i == 0:
            path[:, i] = np.array(range(d)) + 1
            print('')
            continue

        for j in range(d):
            print(f'更新节点 ({j}, {i}) 的状态')
            temp = state[:, i - 1] * weight[i - 1, :, j]
            temp_max = max(temp)
            temp_index = np.where(temp == temp_max)
            path[j, i] = temp_index[0] + 1

            state[j, i] = max(temp) * state[j, i]
        print('')

    print(state)
    print(path)


if __name__ == '__main__':
    viterbi(state, weight)