##序言
…
本系列对算法的讲解都会从两篇部分予以呈现:
a. 湿货部分要浅入浅出,形象生动,读得明白。
b. 干货部分要一文以蔽之,公式罗列,看得通透;
下面是(一)的 b 部分内容
#Unigram
Unigram模型认为序列中的每一项都是独立发生的,所以很自然,假设我们有N个序列,每个序列长度是
M
n
M_n
Mn,那么整个序列的联合概率分布就是:
P
(
X
)
=
∏
i
N
∏
j
M
i
p
(
X
i
j
)
P(X) = \prod_i^N\prod_j^{M_i}p\left(X_i^j\right)
P(X)=i∏Nj∏Mip(Xij)
如果
x
i
j
x_i^j
xij的取值是有限的,属于集合
V
V
V,上式可以转化为
P
(
X
)
=
∏
v
p
(
x
=
v
)
c
o
u
n
t
(
v
)
P(X) = \prod_vp(x=v)^{count(v)}
P(X)=v∏p(x=v)count(v)
其中
c
o
u
n
t
(
v
)
count(v)
count(v)表示
v
v
v在序列中的出现次数,上式就是Unigram模型的似然函数,并且它的对数似然函数为:
L
=
l
n
P
(
X
)
=
∑
v
c
o
u
n
t
(
v
)
∗
l
n
p
(
x
=
v
)
并
且
∑
v
p
(
v
)
=
1
L = lnP(X) = \sum_vcount(v)*ln^{p(x=v)}\\ 并且 \sum_vp\left(v\right) = 1
L=lnP(X)=v∑count(v)∗lnp(x=v)并且v∑p(v)=1
我们将限制条件通过拉格朗日算子加到对数似然函数里并分别对参数求导:
L
′
=
l
n
P
(
X
)
=
∑
v
c
o
u
n
t
(
v
)
∗
l
n
p
(
v
)
+
λ
(
1
−
∑
v
p
(
v
)
)
∂
L
′
∂
p
(
v
)
=
c
o
u
n
t
(
v
)
p
(
v
)
−
λ
∂
L
′
∂
λ
=
1
−
∑
v
p
(
v
)
\begin{aligned} L' = lnP(X) &= \sum_vcount(v)*ln^{p(v)} + \lambda(1-\sum_vp\left(v\right))\\ \frac{\partial L'}{\partial p(v)} &= \frac{count(v)}{p(v)}-\lambda\\ \frac{\partial L'}{\partial \lambda} &= 1-\sum_vp\left(v\right) \end{aligned}
L′=lnP(X)∂p(v)∂L′∂λ∂L′=v∑count(v)∗lnp(v)+λ(1−v∑p(v))=p(v)count(v)−λ=1−v∑p(v)
令两个偏导为0,我们先有
p
(
v
)
=
c
o
u
n
t
(
v
)
λ
并
且
∑
v
p
(
v
)
=
∑
v
c
o
u
n
t
(
v
)
λ
=
1
所
以
λ
=
c
o
u
n
t
(
∗
)
p(v)=\frac{count(v)}{\lambda} 并且\\ \sum_vp\left(v\right) = \sum_v\frac{count(v)}{\lambda} =1\\ 所以\lambda = count(*)
p(v)=λcount(v)并且v∑p(v)=v∑λcount(v)=1所以λ=count(∗)
所以Unigram模型的最大似然估计就是
p
(
v
)
=
c
o
u
n
t
(
v
)
c
o
u
n
t
(
∗
)
p(v) = \frac{count(v)}{count(*)}
p(v)=count(∗)count(v)
这是一个非常符合直觉的公式,一个term出现的概率就是它在训练数据里的频率,所以甚至有人会觉得这就是常识,但实际上背后是有数学推导支撑的。
#马尔可夫模型
按照上面类似的逻辑,一阶马尔可夫的最大似然估计就是
p
(
x
t
=
v
i
,
x
t
+
1
=
v
j
)
=
c
o
u
n
t
(
v
i
,
v
j
)
c
o
u
n
t
(
v
i
,
∗
)
p(x^{t}=v_i,x^{t+1}=v_j) = \frac{count(v_i,v_j)}{count(v_i,*)}
p(xt=vi,xt+1=vj)=count(vi,∗)count(vi,vj)
这里不作推导了,有兴趣可以自己推导一下。(多说一句,很多书上上面这两个公式都是直接给出来的,但你自己从头推导过一次后会感觉概率论这东西还是靠谱的……233)
#隐马尔可夫模型HMM
根据我们a部分的描述,隐马尔可夫链其实是有两条序列的,我们分别用
H
H
H和
O
O
O来表示,以一阶隐马尔可夫链为例:
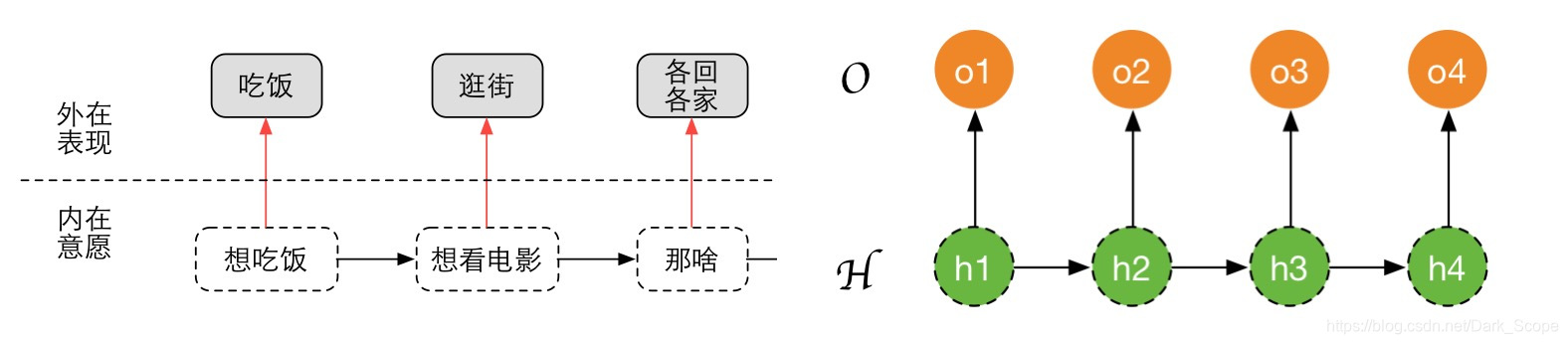
那么对于某个训练样本
{
o
,
h
}
\{o,h\}
{o,h}它的联合概率应该如何表示呢
P
(
o
,
h
∣
θ
)
=
p
(
h
1
∣
θ
)
∏
t
=
2
T
p
(
h
t
∣
h
t
−
1
,
θ
)
∏
t
=
1
T
p
(
o
t
∣
h
t
,
θ
)
P(o,h|\theta) = p(h_1|\theta)\prod_{t=2}^Tp(h_t|h_{t-1},\theta)\prod_{t=1}^Tp(o_t|h_t,\theta)
P(o,h∣θ)=p(h1∣θ)t=2∏Tp(ht∣ht−1,θ)t=1∏Tp(ot∣ht,θ)
主要是三个部分:1)第一个隐藏层的初始状态。2)隐藏层的转移概率。3)从隐藏层到表示层的表现概率,我们分别用特殊的符号来标记对应的参数:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \pi_{q_i} &= p…
所以上面的联合概率公式可以表示为:
P
(
o
,
h
∣
θ
)
=
π
h
1
∏
t
=
2
T
A
h
t
−
1
h
t
∏
t
=
1
T
B
h
t
o
t
P(o,h|\theta) = \pi_{h_1}\prod_{t=2}^TA_{h_{t-1}h_t}\prod_{t=1}^TB_{h_to_t}
P(o,h∣θ)=πh1t=2∏TAht−1htt=1∏TBhtot
如果我们同时知道
{
o
,
h
}
\{o,h\}
{o,h},想要求得
θ
\theta
θ,那其实问题很简单,无非就是类似Unigram和Bigram统计一下各个term和pair出现的次数,并计算出概率。
但问题的关键来了:在实际中我们多半是不知道隐藏层状态是什么样的,否则它们就不叫「隐藏层」了,所以我们只能期望表现序列
o
o
o的概率最大:
p
(
o
∣
θ
)
=
∑
h
p
(
o
,
h
∣
θ
)
p(o|\theta) = \sum_hp(o,h|\theta)
p(o∣θ)=h∑p(o,h∣θ)
记住h可是一个序列,在任何一个位置的取值都有
∣
Q
∣
|Q|
∣Q∣种,所以对于一个长度为N的序列,我们需要加和的隐藏层候选集大小为
∣
Q
∣
T
|Q|^T
∣Q∣T(T是序列长度),这是一个极其庞大的数字。而且当
h
h
h的状态不同时,从
h
h
h表现为
o
o
o的概率也不一样。所以我们想直接去最大化这个联合分布(最大似然)是不现实的。
#Baum-Welch算法(EM算法)
所以在这里只能通过EM算法,去一步步迭代计算求得
θ
\theta
θ,EM算法首先假设参数是知道的,然后最大化Q函数来更新参数值(Baum-Welch是EM算法在HMM中的具体实现)
EM算法作为十大数据挖掘算法之一,后面我们可以单独开一篇博客学习,我自己现在也没有理解得很深入,但在这里你只需要知道它有两步,Q&M,Q步骤中计算Q函数,M步骤中最大化Q函数。
在HMM问题中,
θ
o
l
d
是
已
知
的
,
θ
是
我
们
需
要
去
求
解
的
\theta^{old}是已知的,\theta是我们需要去求解的
θold是已知的,θ是我们需要去求解的,第一个公式里可以认为是Q函数的定义:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ Q(\theta,\thet…
公式复杂度似乎有些不可控了,我们单把上式的第一部分拎出来:
F
=
∑
h
p
(
h
∣
o
,
θ
o
l
d
)
∗
l
n
π
h
1
F = \sum_h p(h|o,\theta^{old})*ln\ \pi_{h_1}
F=h∑p(h∣o,θold)∗ln πh1
假设我们指定
h
1
=
q
h_1=q
h1=q
则F中和
h
1
=
q
h_1=q
h1=q 相关的部分就是
∑
h
∈
H
q
′
p
(
h
∣
o
,
θ
o
l
d
)
∗
l
n
π
q
\sum_{h \in H'_q} p(h|o,\theta^{old})*ln\ \pi_{q}
h∈Hq′∑p(h∣o,θold)∗ln πq
H
q
′
H'_q
Hq′是
H
H
H中
h
1
=
q
h_1=q
h1=q的所有可能的
h
h
h序列构成的集合,此时
∑
h
∈
H
′
p
(
h
∣
o
,
θ
o
l
d
)
\sum_{h \in H'} p(h|o,\theta^{old})
∑h∈H′p(h∣o,θold)发生了微妙的变化:
∑
h
∈
H
′
p
(
h
∣
o
,
θ
o
l
d
)
=
p
(
h
1
=
q
∣
o
,
θ
o
l
d
)
\sum_{h \in H'} p(h|o,\theta^{old}) = p(h_1=q|o,\theta^{old})
h∈H′∑p(h∣o,θold)=p(h1=q∣o,θold)
所以原式F:
F
=
∑
q
p
(
h
1
=
q
∣
o
,
θ
o
l
d
)
l
n
π
q
F = \sum_qp(h_1=q|o,\theta^{old})ln\ \pi_q
F=q∑p(h1=q∣o,θold)ln πq
类似的方法我们可以吧
Q
(
θ
,
θ
o
l
d
)
Q(\theta,\theta^{old})
Q(θ,θold)变成下式:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ Q(\theta,\…
为了方便后续计算表示,我们用:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \gamma_t &= p(…
所以:
Q
(
θ
,
θ
o
l
d
)
=
∑
q
γ
1
(
q
)
l
n
π
q
+
∑
t
=
2
∑
q
1
∈
Q
∑
q
2
∈
Q
ξ
t
(
q
1
,
q
2
)
∗
l
n
A
q
1
,
q
2
+
∑
t
∑
q
γ
t
(
q
)
l
n
B
q
,
o
t
Q(\theta,\theta^{old}) = \sum_q\gamma_1(q)ln\ \pi_q + \sum_{t=2}\sum_{q_1 \in Q}\sum_{q_2 \in Q}\xi_t(q_1,q_2)*lnA_{q_1,q_2} + \sum_{t}\sum_q\gamma_t(q)ln\ B_{q,o_t}
Q(θ,θold)=q∑γ1(q)ln πq+t=2∑q1∈Q∑q2∈Q∑ξt(q1,q2)∗lnAq1,q2+t∑q∑γt(q)ln Bq,ot
然后我们最大化Q,分别对每个参数进行求导,将限定(主要是各种概率和为1)以拉格朗日乘子的方式加入,比如对
π
q
\pi_q
πq求导:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \frac{\partial…
类似的方式可以分别求得:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ A_{q_1,q_2} &=…
上面三个公式就是我们在EM算法的M步骤中更新参数值的公式。
但在这里,我们遗留了一个很重要的问题,
γ
和
ξ
\gamma和\xi
γ和ξ应该如何计算呢,我们只是为了简化公式引入的这两个符号,它们背后还是概率公式啊。
#前向后向算法(forward-backward)
所以接下来我们就要解决这个问题,就是如何计算
γ
\gamma
γ和
ξ
\xi
ξ,也就是在知道了表现序列
o
o
o和相关参数
θ
o
l
d
\theta^{old}
θold后,想要知道和
h
h
h相关的一些概率。
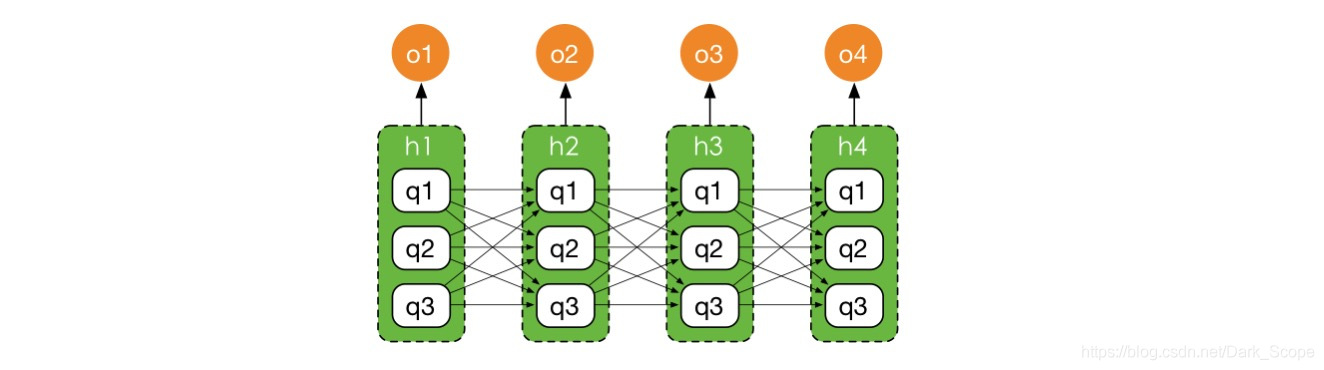
上面是一个示意图,
∣
Q
∣
=
3
|Q|=3
∣Q∣=3,每个隐藏状态的取值都有3种情况,所以下面就变成了那样一个全连接的网络,看起来有点像一个NN了。
有(下面公式省略
θ
o
l
d
\theta^{old}
θold):
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \gamma_t &…
上式分母中的部分其实跟
θ
o
l
d
\theta^{old}
θold没啥关系,我们把分子的两部分分别定义为
α
\alpha
α和
β
\beta
β:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \alpha(h_t…
其中
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \alpha(h_t…
上面推导过程用到的性质无非是马尔可夫假设和条件概率的概念而已,此时我们已经发现
α
\alpha
α是可以迭代进行计算的了,整个计算过程是从前往后的,所以是前向算法,其实也很好理解,比如下图的a中标红的节点
h
3
=
q
2
h_3=q_2
h3=q2,其实只能从
h
2
h_2
h2几个状态转移过来,箭头的参数值就是
p
(
h
3
=
q
2
∣
h
2
=
q
)
p(h_3=q_2|h_{2}=q)
p(h3=q2∣h2=q),也就是A可以指示的。
对于序列的第一个隐藏状态,它的初始值就是
α
(
h
1
)
q
=
π
q
∗
p
(
o
1
∣
q
)
\alpha(h_1)^q = \pi_q*p(o_1|q)
α(h1)q=πq∗p(o1∣q)
类似的方法我们可以推导得到
β
\beta
β,这是后向算法的部分,示意图如下面图(b)所示:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \beta(h_t)…

现在回头去看就有
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \gamma_t(q…
而
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ \xi_t(q_1,…
可以看到,前向后向算法我们一开始的意图已经达到了,而实际上前向后向算法也可以用来计算出当所有参数给定时,o的概率,这在实际应用中我们判断一个序列出现的概率时非常有用:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ p(o) &= \s…
至此,我们已经得到
γ
\gamma
γ和
ξ
\xi
ξ了,所以完全可以带回到EM算法去迭代地学习到模型中的参数集合
θ
=
{
A
,
B
,
π
}
\theta=\{A,B,\pi\}
θ={A,B,π}了。但在实际的应用中,我们通常希望给出一个观测序列
o
o
o,可以知道对应概率最大的
h
h
h是什么,因为
h
h
h有可能是一些有意义的状态比如单词词性、语音词之类的东西,在湿货部分的例子里就是我们希望通过表现外在行为去猜测其最大可能的内在意愿,这也是我们人在日常生活中潜意识会干的事情。
#Viterbi算法
如何解决上一节提到的问题呢,最简单的方法,我们不是知道
γ
t
(
q
)
\gamma_t(q)
γt(q)是t时刻隐状态为q的概率吗,对于每一个时刻我们找一个最大的q不就好了。也就是
q
t
∗
=
arg
max
q
i
[
γ
t
(
q
i
)
]
q_t^* = \mathop{\arg\max}_{q_i}[\gamma_t(q_i)]
qt∗=argmaxqi[γt(qi)]
这样的做法被称为**「近似算法」,但我们知道,所有可能的序列有
∣
Q
∣
T
|Q|^T
∣Q∣T种,近似算法不能保证求得的解是整体序列概率最大的那一个。说白了,我们希望找到的是下面概率图(c)(注意此时的连线已经不是转移概率了)中的一个最优路径**(概率累乘最大)
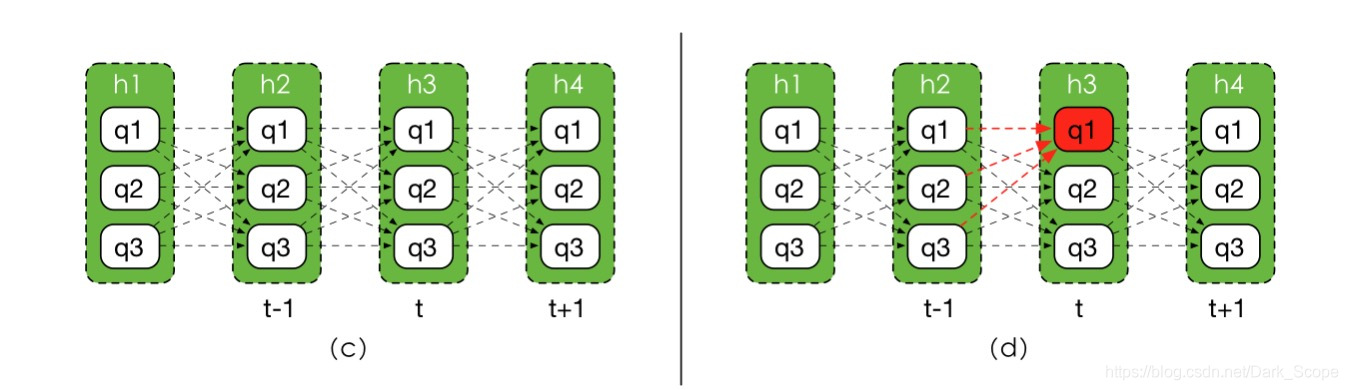
一提到最优路径,做过OI/ACM题目的同学可能都会想到动态规划,没错,这里我们就要通过动态规划来求解,在序列算法中被称为Viterbi算法。
首先我们定义一个概率计算函数
f
t
(
q
)
f_t(q)
ft(q)表示在
h
t
=
q
h_t=q
ht=q的前提下从1到t所有序列中最大概率值:
f
t
(
q
)
=
max
h
1...
t
−
1
p
(
h
t
=
q
,
o
1...
t
)
f_t(q) = \mathop{\max}_{h_{1...t-1}}p(h_t=q,o_{1...t})
ft(q)=maxh1...t−1p(ht=q,o1...t)
在上面那个图(d)中,我们想求到
f
3
(
q
1
)
f_3(q_1)
f3(q1),你会发现它只能从前一个隐藏状态的三种可能性转移过来,我们只需要看哪个
q
′
q'
q′的
f
t
−
1
(
q
′
)
∗
A
q
′
,
q
f_{t-1}(q')*A_{q',q}
ft−1(q′)∗Aq′,q更大就好了,至于
f
t
−
1
(
q
′
)
f_{t-1}(q')
ft−1(q′)怎么求解我并不关心,交给递归就好了,这就是递归算法无后效性的体现。
f
t
(
q
)
=
(
max
q
′
f
t
−
1
(
q
′
)
∗
A
q
′
,
q
)
∗
B
q
,
o
t
f_t(q) = \left(\mathop{\max}_q'f_{t-1}(q')*A_{q',q}\right)*B_{q,o_t}
ft(q)=(maxq′ft−1(q′)∗Aq′,q)∗Bq,ot
对于第一个状态,初始值为
f
1
(
q
)
=
π
q
∗
B
q
,
o
1
f_1(q) = \pi_q*B_{q,o_1}
f1(q)=πq∗Bq,o1
这样直到最后,我们从
f
T
(
q
)
f_T(q)
fT(q)中找一个概率最大的就是我们求解最优路径的值了。
等等,我们是想找到最优路径本身,你算一个最大概率值算怎么回事啊?其实要得到最优路径也很简单,我们只需要在计算
f
t
(
q
)
f_t(q)
ft(q)顺带记录一下最大的概率是从之前哪个状态转移过来的就好了,令:
g
t
(
q
)
=
arg
max
q
′
f
t
−
1
(
q
′
)
∗
A
q
′
,
q
g_t(q) = \mathop{\arg\max}_{q'}f_{t-1}(q')*A_{q',q}
gt(q)=argmaxq′ft−1(q′)∗Aq′,q
g
t
(
q
)
g_t(q)
gt(q)表示当t时刻隐藏状态确认是q的情况下,它的上一时刻状态应该是什么,我们最后在
f
T
(
q
)
f_T(q)
fT(q)找到一个概率最大的q,只需要要根据这个q一步步回溯回去就可以找到对应的序列了,如图e所示,我们在最后一步挑选了q1。

#尾巴
隐马尔可夫模型在语音识别、NLP等领域有着非常广泛的应用,序列算法里未来还有其它跟「隐变量」打交道的东西,隐马尔可夫应该算经典之一。
之前在不同的书上都看过多次隐马尔可夫模型,但记忆不深刻,时间稍微一长就忘掉了,所以借着这个机会从头到尾梳理一次,按照概率表示)->(EM算法)->(前向后向算法)->(Viterbi)这个顺序理解相当酣畅,都是有需求才进入下一步的介绍,承上启下,相信这次要记得久一点了。
在过程中参考了《PRML》和《统计学习方法》,发现书上并不一定按照这个思路来讲,不是很好串起来,而且一些概率公式之间跳的太快(估计是我数学比较渣)或者压根没有,这次从头搞一次,我感觉应该是比较丰实了。






















 262
262











 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








