【机器学习】支持向量机（3）——线性支持向量机（软间隔最大化，对偶算法）

前言

此文介绍了线性可分支持向量机的硬间隔最大化以及它的对偶算法，很好的理解线性可分支持向量机是理解线性支持向量机的基础，只要理解前面的，后面的就会很容易理解。

首先，前面我们所讨论的都是基于线性可分的训练数据集，但在现实任务中，我们得到的一般都不是线性可分的，这是线性可分支持向量机就不适用了。因为这时我们之前所提到的不等式约束并不能都成立。

缓解该问题的一个办法就是允许支持向量机在一些样本上出错。那么我们怎样才能将它扩展到线性不可分问题呢？这就需要我们将硬间隔最大化改为软间隔最大化

软间隔

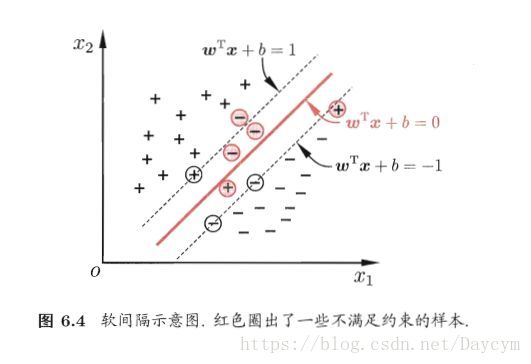
图片来源：周志华《机器学习》

我们之前提到的硬间隔，是要求所有样本都满足约束条件，而软间隔则是允许某些样本不满足约束：
$$y_i(w\cdot x_i+b)⩾1$$
自然，在最大化间隔的同时，不满足约束的样本应尽可能的少。

为了解决某些样本不满足约束条件，可以对每个样本点 $(x_i,y_i)$ 引入一个松弛变量 ${\xi }_i⩾0$，是函数间隔加上松弛变量大于等于1，这样，约束条件就变为：
$$y_i(w\cdot x_i+b)⩾1-{\xi }_i$$
同时，对每个松弛变量 ${\xi }_i$，支付一个代价 ${\xi }_i$ 。目标函数由原来的$\frac{1}{2}||w|{|}^2$变成：
$$\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i$$
这里，$C>0$称为惩罚系数，$C$值大时对误分类的惩罚增加，$C$值小时对误分类的惩罚减小。

此时，最优化的目标函数包括两个含义：

• 使$\frac{1}{2}||w|{|}^2$尽量小即间隔尽量大
• 使误分类点的个数尽量小

$C$是调和二者的系数

有了上面的思路，可以和线性可分支持向量机一样来考虑线性支持向量机的学习问题。

线性不可分的线性支持向量机的学习问题就变为如下凸二次规划问题（原始问题）：

$$\begin{gathered} \underset{w,b,\xi }{\min }\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i \\ s.t.y_i(w\cdot x_i+b)⩾1-{\xi }_i，i=1,2,...,N \\ {\xi }_i⩾0，i=1,2,...,N \end{gathered}$$

通过求解以上凸二次规划问题，即软间隔最大化问题，得到的分离超平面为：

$$w^{\ast }\cdot x+b^{\ast }=0$$
以及相应的分类决策函数：
$$f(x)=sign(w^{\ast }\cdot x+b^{\ast })$$
这就称为：线性支持向量机

对偶算法

对偶问题的构建和线性可分支持向量机的对偶问题的构建类似。

为了让大家更容易理解，现在我们再来构建一次：

（1）首先构建拉格朗日函数
$$L(w,b,\xi ,\alpha ,\mu )=\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i-\sum _{i=1}^N{\alpha }_i(y_i(w\cdot x_i+b)-1+{\xi }_i)-\sum _{i=1}^N{\mu }_i{\xi }_i$$
其中，${\alpha }_i⩾0，{\mu }_i⩾0$

（2）求${\min }_{w,b,\xi }L(w,b,\xi ,\alpha ,\mu )$

拉格朗日函数$L(w,b,\xi,\alpha,\mu) $依次对$w,b,\xi$求偏导数并令为0：
$$\begin{gathered} {\nabla }_{w}L(w,b,\xi ,\alpha ,\mu )=w-\sum _{i=1}^N{\alpha }_i{y}_i{x}_i=0 \\ {\nabla }_{b}L(w,b,\xi ,\alpha ,\mu )=-\sum _{i=1}^N{\alpha }_i{y}_i=0 \\ {\nabla }_{{\xi }_i}L(w,b,\xi ,\alpha ,\mu )=C-{\alpha }_i-{\mu }_i=0 \end{gathered}$$
得：
$$\begin{gathered} w=\sum _{i=1}^N{\alpha }_i{y}_i{x}_i \\ \sum _{i=1}^N{\alpha }_i{y}_i=0 \\ C-{\alpha }_i-{\mu }_i=0 \end{gathered}$$

代入拉格朗日函数，得：
$$\underset{w,b,\xi }{\min }L(w,b,\xi ,\alpha ,\mu )=-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)+\sum _{i=1}^N{\alpha }_i$$

（3）再对${\min }_{w,b,\xi }L(w,b,\xi ,\alpha ,\mu )$求$\alpha$的极大，即得对偶问题：
$$\begin{gathered} \underset{\alpha }{\max }-\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)+\sum _{i=1}^N{\alpha }_i \\ s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0 \\ C-{\alpha }_i-{\mu }_i=0 \\ {\alpha }_i⩾0 \\ {\mu }_i⩾0，i=1,2,...,N \end{gathered}$$
将上式的目标函数由求极大转换为求极小，再将约束条件合并，得到等价的对偶最优化问题：
$$\begin{gathered} \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^N{\alpha }_i \\ s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0 \\ 0⩽{\alpha }_i⩽C，i=1,2,...,N \end{gathered}$$

线性支持向量机对偶算法：

输入：线性可分训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , . . . , ( x N , y N ) } T = \{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\} T={(x1​,y1​),(x2​,y2​),...,(xN​,yN​)}，其中， x i ∈ X = R n ， y i ∈ Y = { − 1 , + 1 } ， i = 1 , 2 , . . . , N x_i \in \mathcal{X} = R^n，y_i \in \mathcal{Y}=\{-1,+1\}，i=1,2,...,N xi​∈X=Rn，yi​∈Y={−1,+1}，i=1,2,...,N；
输出：最大间隔分离超平面和分类决策函数。
（1）选择惩罚系数 $C > 0 $ ，构造并求解约束最优化问题：
$$\begin{gathered} \underset{\alpha }{\min }\frac{1}{2}\sum _{i=1}^N\sum _{j=1}^N{\alpha }_i{\alpha }_j{y}_i{y}_j(x_i\cdot x_j)-\sum _{i=1}^N{\alpha }_i \\ s.t.\sum _{i=1}^N{\alpha }_i{y}_i=0 \\ 0⩽{\alpha }_i⩽C，i=1,2,...,N \end{gathered}$$
求得最优解${\alpha }^{\ast }=({\alpha }_1^{\ast },{\alpha }_2^{\ast },...,{\alpha }_N^{\ast }{)}^T$；
（2）计算：
$$w^{\ast }=\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i{x}_i$$
并选择${\alpha }^{\ast }$的一个分量 $\alpha_j^* $ 适合条件$0<{\alpha }_j^{\ast }<C$，计算：
$$b^{\ast }=y_j-\sum _{i=1}^N{\alpha }_i^{\ast }{y}_i(x_i\cdot x_j)$$
（3）求得分离超平面：
$$w^{\ast }\cdot x+b^{\ast }=0$$
分类决策函数：
$$f(x)=sign(w^{\ast }\cdot x+b^{\ast })$$

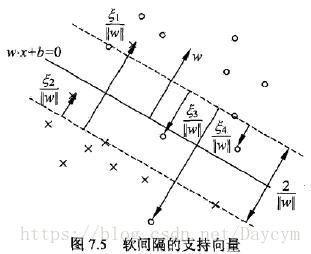
软间隔支持向量

软间隔的支持向量 $x_i$ 或在间隔边界上，或在间隔边界与分离超平面之间，或在分离超平面误分一侧。

• 若${\alpha }_i^{\ast }<C$，则 ${\xi }_i=0$ ，支持向量 $x_i$ 恰好落在间隔边界上；
• 若${\alpha }_i^{\ast }=C$， $0<{\xi }_i<1$ ，则正确分类，支持向量 $x_i$ 在间隔边界与分离超平面之间；
• 若${\alpha }_i^{\ast }=C$， ${\xi }_i=1$ ，支持向量 $x_i$ 在分离超平面上；
• 若${\alpha }_i^{\ast }=C$， ${\xi }_i>1$ ，支持向量 $x_i$ 在分离超平面误分一侧；

合页损失函数

线性支持向量机学习还有另外一种解释，就是最小化以下目标函数：
$$\sum _{i=1}^N[1-y_i(w\cdot x_i+b){]}_{+}+\lambda ||w|{|}^2$$
目标函数第一项是经验损失或经验风险，称为合页损失函数。下标“+”表示一下取正值的函数：
$$[z{]}_{+}=\{\begin{array}{l}z,z>0\\ 0,z⩽0\end{array}$$

这就是说，当样本点$(x_i,y_i)$被正确分类且函数间隔（确信度）$y_i(w\cdot x_i+b) $大于1时，损失是0，否则损失为$1-y_i(w\cdot x_i+b)$，我们注意到上图中实例点$x_4$被正确分类，但是在间隔边界与分离超平面之间，损失不是0，目标函数第二项是系数$\lambda$的$w$的$L_2$范数，是正则化项。

两个方式的相互转换：

定理： 线性支持向量机原始最优化问题：
$$\begin{gathered} \underset{w,b,\xi }{\min }\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i \\ s.t.y_i(w\cdot x_i+b)⩾1-{\xi }_i，i=1,2,...,N \\ {\xi }_i⩾0，i=1,2,...,N \end{gathered}$$
等价于最优化问题：
$$\underset{w,b}{\min }\sum _{i=1}^N[1-y_i(w\cdot x_i+b){]}_{+}+\lambda ||w|{|}^2$$

证明：
令：$$[1-y_i(w\cdot x_i+b){]}_{+}={\xi }_i$$
则 ${\xi }_i⩾0，$式$ \ \xi_i \geqslant 0$成立；
当$1-y_i(w \cdot x_i + b ) > 0 $时，有$y_i(w \cdot x_i + b ) = 1 - \xi_i$；
当$1-y_i(w \cdot x_i + b ) \leqslant 0 $时，$\xi_i = 0$ ，有$y_i(w\cdot x_i+b)⩾1-{\xi }_i$；
故：$w,b,{\xi }_i$ 满足约束条件，所以最优化问题：
$$\underset{w,b}{\min }\sum _{i=1}^N[1-y_i(w\cdot x_i+b){]}_{+}+\lambda ||w|{|}^2$$
可写为：
$$\underset{w,b}{\min }\sum _{i=1}^N{\xi }_i+\lambda ||w|{|}^2$$
若取$\lambda =\frac{1}{2C}$，则：
$$\underset{w,b}{\min }\frac{1}{C}(\frac{1}{2}||w|{|}^2+C\sum _{i=1}^N{\xi }_i)$$
与原始问题等价。

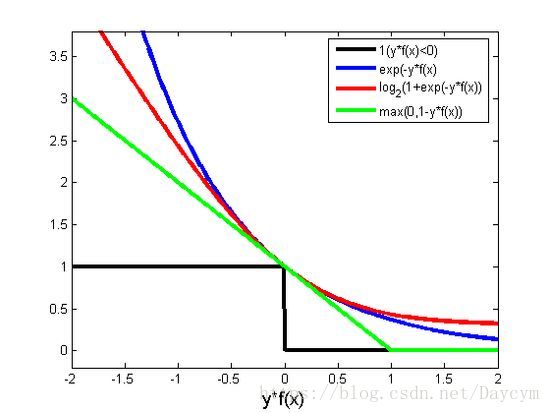
常用的合页损失函数有：

• hinge损失：${\ell }_{h}inge(z)=max(0,1-z)$
• 指数损失：${\ell }_{e}xp(z)=exp(-z)$
• 对数损失：${\ell }_{l}og(z)=log(1+exp(-z))$

函数图像如下图：

参考书籍：
《机器学习》 周志华，《统计学习方法》 李航