高等工程数学 —— 第四章（1）线性方程组的直接解法与广义逆矩阵求解矛盾方程组

梦里一声何处鸿

已于 2022-12-03 15:08:37 修改

阅读量1.1k

点赞数 1

分类专栏：高等工程数学文章标签：矩阵线性代数算法

于 2022-10-25 23:49:07 首次发布

本文链接：https://blog.csdn.net/Deam_swan_goose/article/details/127520864

版权

高等工程数学专栏收录该内容

13 篇文章 42 订阅

订阅专栏

高等工程数学 —— 第四章（1）线性方程组的直接解法与广义逆矩阵求解矛盾方程组

文章目录

高等工程数学 —— 第四章（1）线性方程组的直接解法与广义逆矩阵求解矛盾方程组

线性方程组的直接解法

Gauss消去法

简单而言就是通过初等行变换将增广矩阵转换为上三角矩阵或者下三角矩阵。然后先解出来只有一位未知量的式子，再不断的代入求解就行。

例：
运用Gauss消去法求解下面线性方程组

$\begin{cases} x_1+\frac{2}{3}x_2+\frac{1}{3}x_3 = 2 \\ \frac{9}{20}x_1+x_2+\frac{11}{20}x_3 = 2 \\ \frac{2}{3}x_1+\frac{1}{3}x_2+x_3 = 2\end{cases}$

通过方程组我们可以得到增广矩阵如下：

$\begin{pmatrix} 1 & \frac{2}{3} & \frac{1}{3} & 2 \\ \frac{9}{20} & 1 & \frac{11}{20} & 2 \\ \frac{2}{3} &\frac{1}{3} & 1 & 2\\ \end{pmatrix}$

我们对增广矩阵进行初等行变换后得上三角矩阵（这里化作下三角矩阵也是一样的）为：

$\begin{pmatrix} 1 & \frac{2}{3} & \frac{1}{3} & 2 \\ 0 & \frac{7}{10} & \frac{2}{5} & \frac{11}{10} \\ 0 &0 & \frac{53}{63} & \frac{53}{63} \\ \end{pmatrix}$

将增广矩阵改写为方程组为：
$\begin{cases} x_1+\frac{2}{3}x_2+\frac{1}{3}x_3 = 2 \\ \frac{7}{10}x_2+\frac{2}{5}x_3 = \frac{11}{10} \\ \frac{53}{63} x_3 = \frac{53}{63} \end{cases}$

对于这个方程，我们很容求解：
$\begin{cases} x_1= 1 \\ x_2= 1\\ x_3 = 1 \end{cases}$

但是上述方法有个bug。
在这里插入图片描述为了解决这个问题，我们可以通过行变换选取最大列主元素。

列主元法

其实就是多了一个让最大列元素到对角线位置的过程。

在这里插入图片描述

三角分解法

在这里插入图片描述

Doolittle方法

其实就是先对 $x$ 的系数矩阵 $A$ 进行Doolittle分解得下三角矩阵 $L$ 和上三角矩阵 $R$ .

看道例题就会了：

在这里插入图片描述

Cholesky分解（改进平方根法）

正常的Cholesky分解是得到 $A = LL^H$ 。但是在对角线元素处需要开平方根，这就使得在计算机中的运行比较慢。所以我们对该方法进行了改进，如下：

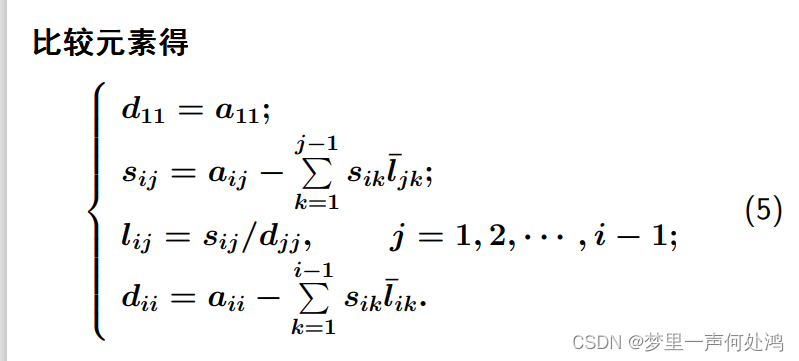
在这里插入图片描述

可见列元素的值不用除以对角线元素
行元素正常，需要用列元素除以对应的对角线元素，然后再转置过去。
算的时候可以先照抄第一列元素，然后第一列非对角线元素除以对角线元素后转置得第一行。
之后就算下一个对角线元素，求其他列元素（不用除以对角线元素），除以后转置得行元素。

例：
在这里插入图片描述
首先对矩阵 $A$ 进行分解。我习惯先把分解得到的上三角矩阵和下三角矩阵写在一起先，因为这样好对照。

在这里插入图片描述

因此得到下三角矩阵 $(L D)$ 为
$\begin{pmatrix} 1 & 0 & 0 & 0 \\ 2 & 1 & 0 & 0 \\ 1 &-2 & 9 & 0 \\ -3 &1 & 6 & 1 \\ \end{pmatrix}$

上三角矩阵 $L^H$ 为

$\begin{pmatrix} 1 & 2 & -1 & -3 \\ 0 & 1 & -2 & 1 \\ 0 & 0 & 1 & \frac{2}{3} \\ 0 &0 &0 & 1 \\ \end{pmatrix}$

根据 $LDL^Hx = b$ 可得 $\begin{cases} (LD)y = b \\ L^Hx = y \end{cases}$

解出来得：
$\begin{cases} y_1 = 1 \\ y_2 = 0\\ y_3 = \frac{5}{3}\\ y_4 = 1 \end{cases}$
$\begin{cases} x_1 = 1 \\ x_2 = 1\\ x_3 = 1\\ x_4 = 1 \end{cases}$

追赶法

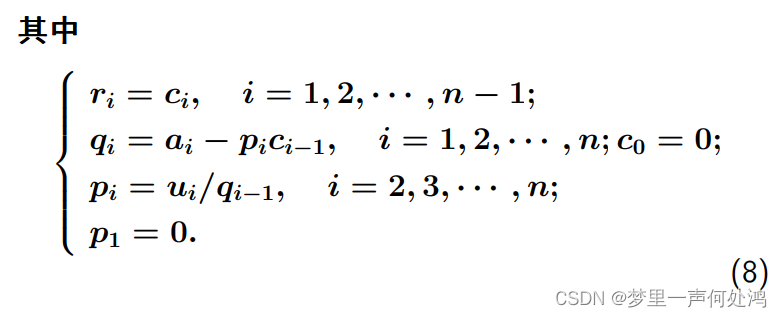
在这里插入图片描述
其实我觉得这些都不用看，你就按Doolittle分解来做就好了。我们看道例题。

例：
在这里插入图片描述
我们就用最基本的Doolittle分解得到下式：

即：
下三角矩阵为
$\begin{pmatrix} 1 & 0 & 0 & 0 \\ -\frac{1}{2} & 1 & 0 & 0 \\ 0 &-\frac{2}{3} & 1 & 0 \\ 0 & 0 & -\frac{3}{4} & 1 \\ \end{pmatrix}$
上三角矩阵为
$\begin{pmatrix} 2 & -1 & 0 & 0 \\ 0 & \frac{2}{3} & -1 & 0 \\ 0 & 0 & \frac{4}{3} & -1 \\ 0 &0 &0 & \frac{5}{4} \\ \end{pmatrix}$

根据 $P Q x = b$ 可得 $\begin{cases} Py = b \\ Qx = y \end{cases}$

解出来得：
$\begin{cases} y_1 = 1 \\ y_2 = \frac{1}{2}\\ y_3 = \frac{1}{3}\\ y_4 = \frac{5}{4} \end{cases}$
$\begin{cases} x_1 = 1 \\ x_2 = 1\\ x_3 = 1\\ x_4 = 1 \end{cases}$