算法基础

 算法基础
什么是算法？

算法（algorithm）一词来自9世纪波斯的数学家Al-khowarizmi（花拉子米）。

算法是一个由人或机器进行的关于某种运算规则的集合。不过只要是为能够得到一个结果而进行运算的系统方法，也都是算法。

    比如许多对布道深感厌烦的英国唱诗班的孩子，就用祈祷书上的算法，来推算耶稣的复活日期，从古希腊起，历史上最著名的算法就是欧几里得的求两个整数最大公约数的算法。

一个算法的执行通常不能包含任何主观的决定，也不能有类似直觉或者创造力等因素掺杂其中。比如，如果一道烹饪菜谱里精确的描述了如果做某一道菜，严格规定了各种原料的数量和精确的烹饪时间的话，那么他也是算法。但是如果他只是有诸如“盐少许”，“把食物煮软”等一些模糊的字眼，那他就不算是一个算法。
不过这条规则有个例外，允许算法在某个特定的情况下，对下一步做什么可以有个随机的选择。需要注意的是，随机并不等于随意，相反，碰到要从多个值中选择的情况下，每个值的概率都应该是已知的，可控制的。算法是不会接受一条诸如“在1-6之间选一个数”而没有提供更多细节的指令的。但是如果说“在1-6之间选一个数，而且每个数被选中的概率都相同”，那么这样的指令就可以接受。计算机中是通过一个伪随机数生成器来实现的。
    后面我们还会看到很多问题没有实用的算法，对于这一类的问题，如果想得到精确的解，采用已知的算法进行计算，大多要花费很长的时间，而一旦碰到此类问题，而又不得不求出解的情况下，我们被迫转而寻找这么一个规则集：在可接受的时间内能算出足够好的近似解。所以有的算法并不是完善的，高效的。
    在研究过算法后，当我们开始着手解决问题时，此时可能有很多的算法可供选择。比如占内存最少的，所用时间最少的，或者容易编程的。也有可能没有那个算法能够完全符合我们的要求，这就需要我们自己去设计算法。
    算法学就是告诉我们如何评估不同的外在因素对可供选择算法的影响，好让我们可以选择出一种最符合特定情况的算法，他也告诉我们如何为一个特定任务设计一种新算法。


算法举例
以初等算数为例
计算981*1234

1）美国算法：  
		

 
 

  
  
 
 

 
 

  
  
 
 

 
 

  
  
 
 

 
 

  
  
 
 

 
 

  
  
 
 

 
 

  
  
 
 

 
 

  
  
 
 



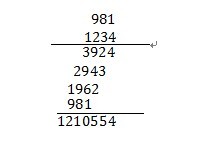
2）英国算法




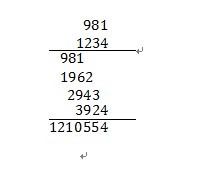
3) 	à la russe 算法


 
 

  
  
 
 

乘数和被乘数写在一起将左边的操作数整除2，将右边的操作数乘以2；接着把左列中商为偶数的行全部删除，最后把右列剩下的数相加，就得到了结果。

4） 分治法
                

     先将被乘数的左半部分09去乘成熟的左半部分12，然后把结果108向左移动，移动的位数就是乘数的位数，然后被乘数的左半部分去乘乘数的有半部分34，移动的位数是乘数位数的一半；第三步将被乘数的有半部分和乘数的左半部分相乘，把结果向左移动乘数位数的一半位，最后用被乘数的有半部分去乘乘数的右半部分，这次的结果不移动，最后把四个结果加起来就是所得到的的结果。

     通过举出上面的例子，想说明的是，即使像初等算数这样简单平常的领域，在操作时也有很多算法可供选择。第一个人从习惯上选择，第二个人从计算简便性选择，第三个人从机器执行角度上选择。
通过对算法性质正式的研究我们就可以在给定情况中明确的选择适当的算法。一个好的选择可以节省时间和金钱；在另一种情况下，当面临着要解决一个复杂问题时，这种选择就可能是成功与失败的区别。
所以如何做出正确的选择，对我们来说至关重要。

 程序符号         
为了让算法更简化，更直接的容易被观察，相同的缩进代表着同一级别的代码，return表示一个过程或一个函数的结束，对于后者来说，他还要带一个函数的返回值。
我们不在过程和函数中声明参数的类型，，也不声明函数的返回值的类型，除非声明这些类型能是程序更加的明了。参数通常是传值调用，这意味着，他们在过程或函数中被看做是局部变量。如果参数前面加上var那就说明他是变量参数，这样他就可以在返回调用程序时，带回一个返回值。
指针用←表示
这里拿   à la russe 算法的程序作为例子
Function russe(m,n)
        result←0
	  repeat
 	     if m 是奇数then result←result+n
	     m←m / 2
             n←n + n
        until m = 1
        return rusult

反证法
欧几里德：存在无穷多个素数。
 
证明：
       假设不存在无穷多个素数
设 P={2,3,5,7 }
X = 2*3*5*7=210
Y= x + 1 = 211
 
P中包含最大的素数且有限
所以 之后不存在素数
Y中的一个约数（比1大的）为d能把Y整除那么这个数肯定能把X整除
但是事实上是不能的
所以假设错误
所以原推论成立
算法实现：
 
 

  
  

 
 
Function New prime (P:整数集合)
			{变量P应该是一个非空有限的素数级}
			X ← P中所有元素的乘积
			Y ← x + 1
			d← 1
			repeat  d ← d + 1 直到d整除Y
			return  d
算法二
Function DumpEuclid (P:整数集合)
			{变量P应该是一个非空有限的素数级}
			X ← P中最大的元素
                        repeat  x ←x + 1 until x是素数
                        return  x

第二个算法如果P中不幸包含了最大的那个素数，则此算法就陷入无限循环中，不过这个算法确实可行

 

定理：存在两个无理数x，y，使得 是一个有理数。

 

假设不存在两个无理数x，y，使得 是一个有理数；

 

证明：

因为 是一个无理数

假设z等于  根据假设可知z是无理数

则w= =2 是有理数，与假设不符

所以原推论成立。

 

 

这里证明z等于 是无理数的情况，依赖于我们开始时的错误假设，因此这个证明是不合法的（实际上z确实是一个无理数，不过很难证实）所以我们必须不能用反证法的中间结果作为结论。

这里没有直接的方法可以从定理证明中求出满足条件的无理数对（x，y）。你所能做的就是选出两对无理数，然后声称你确信他们中之一满足条件。这种证明方法在间接证明中相当常见，我们称它为非构造性证明。即使有些数学家不接受非构造性证明，但是大部分还是认为这种技巧完全合法，不过在任何情况下我们都应该尽量在算法上下文中避免使用。

Brillian整理2013-05-12

本文参考：

《算法基础》

未完待续