【蓝桥杯前一晚，再看一题】一套模板，秒杀并查集问题!

一套模板，秒杀路径存在问题！

写在前面

本文为基于程序员carl所写题解的笔记，原网址 代码随想录

力扣原题链接 1971. 寻找图中是否存在路径

关于题目

题目里面给出了一个用二维vector，或者说二维数组表示的双向图。并不像我们印象中的数组矩阵表示的图，这里只有一对一对的键值对，每个键值对表示一对相互连接的节点。而我们的任务，就是给出两个节点，判断其中是否有连起来的通路。

要解决这个问题，直觉上，我们可以用这些键值对把二维邻接矩阵还原出来，然后在这个图里进行搜索，如果找到了，就说明有通路。当然也可以不还原出矩阵，搜索时在数组里直接遍历也是可以的，只是效率上没那么理想。

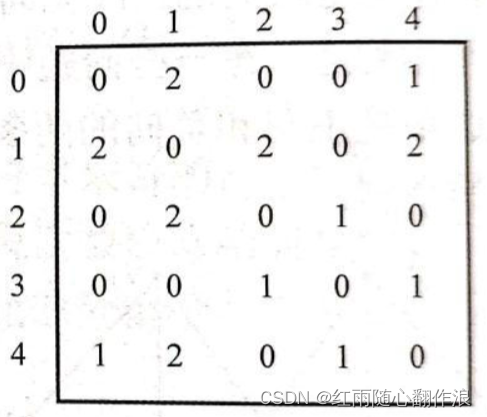
不过，其实我们可以完全不使用搜索，而是使用并查集的方法。使用并查集，只需要一个一维数组就可以了，极大地节省了空间复杂度。

并查集的原理是，一维数组里每个位置下标代表一个节点，数组里存的则是该下标对应的父节点位置。然后通过一直找父节点来找到最高父节点，通过比较两个节点的最高父节点是不是同一个，就可以直接得出答案，极大的节省了时间。

接下来是并查集的模板。首先，题目说节点数量少于20000个，于是先得建立一个该大小的一维数组：

class Solution {
   

	int n = 200005;
	vector<int>father = vector<int>(n,0);

};

然后是并查集的建立部分。首先是初始化。在刚建立时，所有节点都还没有建立起父子关系，因此它们的最高父节点就是自己：

void init() {
   
    for (int i = 0; i < n; ++i) {
   
        father[i] = i;
    }
}

然后是查找父节点的函数：

int find(int u) {
   
    if (father[u] == u) return u; //如果父节点就是自己，那说明自己就是最高父节点了。
    else return find(father[u]); //否则继续找，直到找到最高父节点
}

接下来是重头戏，插入父子节点关系（建立边）的函数：

void join(int u,int v){
   
	u = find(u); //找到最高父节点
	v = find(v); //同上
	if(u == v){
   
		return;	 //如果两人最高父节点是一个，那就没必要插入新边了
	}
	father[v] = u; //否则把v加入u的集合中
}

最后是判断两个节点的最高父节点是否相同的函数。通过这个函数得到最终答案:

bool isSame(int u, int v)<