舞蹈链，DLX算法详解，OJ精讲，详细代码

EQUINOX1

于 2024-01-11 00:14:02 发布

阅读量1.1k

点赞数 34

分类专栏：数据结构与算法文章标签：算法数据结构 c++ 深度优先

本文链接：https://blog.csdn.net/EQUINOX1/article/details/135516015

版权

数据结构与算法专栏收录该内容

85 篇文章 2 订阅

订阅专栏

问题引入

抽奖机

John最近迷上了游戏厅内的抽奖机，抽奖机有着这样的机制：有[1 , 4]4个数字，每次抽奖会抽到3个不重复的数字，而抽奖机内已经内置了若干个中奖数字对<x,y>(<x,y>和<y,x>对应相同奖品)对应不同的奖品，抽到的三个数字中含的中奖数字对的个数就是中的奖品数目。每期抽奖的中奖数字对不同，每期可以进行若干次抽奖，在开奖前无法提前知道中奖数字对。

John对每期的奖品很心动，购买所有奖品的总价格要比进行若干次抽奖的价格高出很多，但他又不能投入大量的零用钱去抽奖，他想知道抽到所有奖品至少要进行几次抽奖。

John通过简单的排列组合发现中奖数字对有C(4,2) = 6种组合，而抽奖得到的数字有C(4,3) = 4种组合，显然如果进行四次抽奖分别抽到4种不同的三个数字，那么一定能够获得全部的6种奖品，那么有没有可能抽三次也有可能获得所有奖品？抽两次呢？

John想到了可以在矩阵上将将上述组合表示出来，行表示抽到的数字组合，列表示内置中奖的数字对，如下图，红色格子代表每种抽奖组合对应的中奖组合

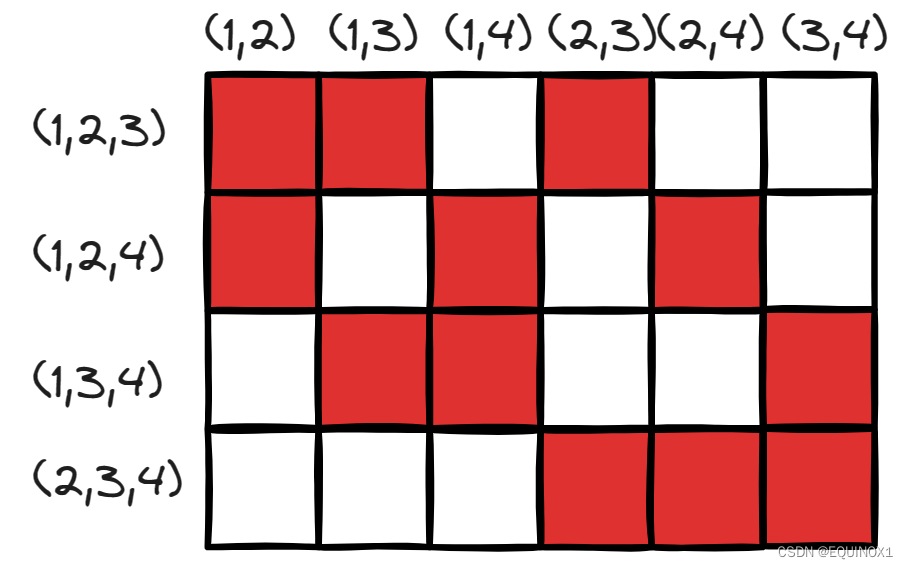
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

John发现如果要获得所有奖品那么抽到的数字组合必须保证每一列都有红色格子覆盖，而通过观察至少需要抽到三种不同数字组合才能使得每一列都有红色格子，于是他便兴冲冲地跑去进行了三轮抽奖，结果三次都是(2,3,4)，获得了三个相同的奖品，他哭死，发誓以后再也不来游戏厅了。

上面的问题中，抽到所有奖品的最少抽奖次数其实就是在矩阵中选择若干行，使得每一列都有红色格子覆盖的最小行数，上面的问题就是经典的重复覆盖问题，而重复覆盖问题要先从精确覆盖问题开始介绍。

精确覆盖问题

精确覆盖的定义

**精确覆盖问题(Exact Cover Problem)**是指给定许多集合Si(1 ≤ i ≤ n)以及一个集合X，求满足以下条件的无序多元组(T1,T2,…,Tm):

∀i，j∈[1 , m]，Ti ∩ Tj = ∅(i != j)
X = T1 ∪ T2 ∪……Tm
∀i ∈ [1 , m]，Ti ∈ {S1 , S2 , …… , Sn}

精确覆盖经典问题

给定一个m行n列的矩阵，矩阵中每个元素要么是1，要么是0。你需要在矩阵中挑选出若干行，使得对于矩阵的每一列 j，在你挑选的这些行中，有且仅有一行的第 j 个元素为1。(亦即保证每列1的个数不重不漏)

和我们抽奖机的问题很像，只不过前者可以重复，而这个问题不能重复。那么我们如何求解呢？

暴力枚举

以我们朴素的思想而言，最容易想到的方法自然是暴力枚举，每一行都有选与不选两种情况。那么总的情况就是2^m，枚举每种情况后进行合法性检查，检查最坏的时间复杂度为O(mn)，那么整体就是O(mn * 2 ^ m)

这个时间复杂度我们显然是接受不了的，那么我们如何优化呢？

状态压缩

每一行我们其实都可以用一个n位的二进制整数bit来表示出状态，第i列如果是1，那么从右至左第i位就是1，否则是0，这样对于合法情况有：

∀i , j，有biti & bitj = 0
bit1 & …… bitn = 2^n - 1

回溯法

我们可以确认一个事实：如果第i行被选了，那么所有和第i行有相同列都是1的行都不能选

这是显然的，那么我们暴力枚举的步骤就可以变为这样的一种回溯法：

选取第i行，删除相关行，相关列
继续深搜
恢复相关行

比如如下的例子：

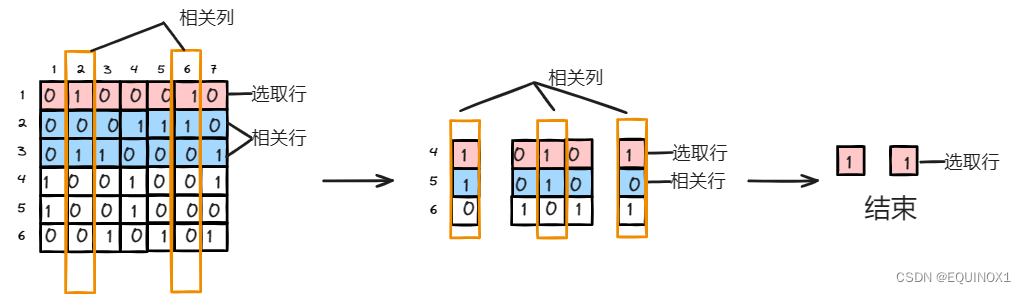
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

Dancing links X算法

X算法

用回溯法解决精确覆盖问题是Donald Knuth提出的，称为“X算法”，它是一个深度优先的不确定性的回溯算法。

算法流程如下：

如果矩阵g没有列（即空矩阵），则当前记录的解为一个可行解；算法终止，返回true；
否则选择矩阵g中“1”的个数最少的列c；（确定性选择）
如果存在g[r][c]=1的行r，将行r放入可行解，进入步骤3；（不确定性选择）
如果不存在g[r][c]=1的行r，即所选列无法被覆盖，则剩下的矩阵不可能完成精确覆盖，说明之前的选择有错（或者根本就无解），需要回溯，并且恢复此次删除的行和列，然后跳到步骤2.1；
对于所有的满足g[r][j]=1的列j，对于所有满足g[i][j]=1的行i，将行i从矩阵A中删除，即前面回溯法中的操作；
如果始终没有进入1，那么返回false

选择列为确定性选择是因为每一列都要被覆盖，所以我们枚举没有被删除的列是确定的

枚举行为不确定性选择是因为枚举改行不一定有解，所以在试错后可能要进行回溯恢复删除

X算法的搜索树表示

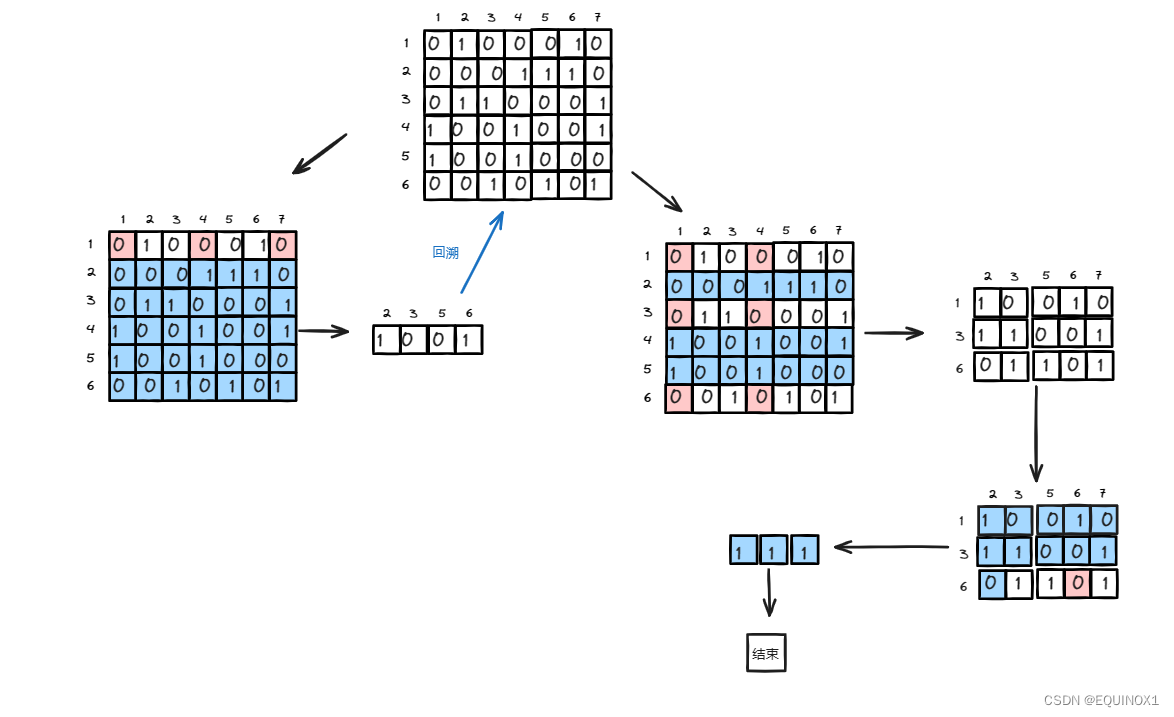
外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传

Dancing Links

X算法的逻辑不算很复杂，那么如何进行实现呢？

如果我们直接在矩阵上进行修改，对于这种顺序存储结构，大量多次地进行删除恢复，太过于繁琐，所以Donald Knuth提出使用链式存储结构来实现——舞蹈链（Dancing Links），因而这一算法也被命名为DLX（Dancing Links X）算法。

双向循环十字链表

舞蹈链其实就是双向循环十字链表，由于我们的回溯过程中要进行大量的删除和恢复，在链表上各个指针之间反复横跳如精美舞蹈，所以舞蹈链这一名称十分贴切。

节点定义

为了在OJ中有着更佳的效率，我们采用静态实现。

int m, n, cnt = 0;                      // 行列，点编号
int u[N]{0}, d[N]{0}, l[N]{0}, r[N]{0}; // 上下左右指针域
int row[N], col[N];                     // 行号，列号
int h[505]{0};                          // 行哨兵节点
int s[505]{0};                          // 列节点数

列哨兵节点初始化

哨兵节点可以帮助我们O(1)尾插

void init() //
{
    for (int y = 0; y <= n; y++)
    {
        u[y] = d[y] = y;
        l[y] = y - 1, r[y] = y + 1;
    }
    l[0] = n, r[n] = 0;
    cnt = n;
}

节点插入

就是在对应行对应列分别进行尾插

void link(int x, int y) // x行y列插入点
{
    row[++cnt] = x, col[cnt] = y; // 记录行号列号
    s[y]++;                       // y列点+1
    u[cnt] = u[y], d[u[y]] = cnt;
    d[cnt] = y, u[y] = cnt; // 列尾插
    // 行尾插
    if (!h[x])
        h[x] = r[cnt] = l[cnt] = cnt;
    else
    {
        l[cnt] = l[h[x]], r[l[h[x]]] = cnt;
        r[cnt] = h[x], l[h[x]] = cnt;
    }
}

DLX算法的实现

舞蹈链是通过dance操作来进行列选择和行列删除，递归回溯来实现DLX算法的，我们自然要实现对应的操作。

删除

即删除所选列y，和所有的列y为1的行

对于所选列y，我们直接删除哨兵节点左右对其的链接，保留哨兵节点对左右的链接，便于后面恢复

由于列y的哨兵节点已经删除，所以第y列的节点不必删除，只需删除相关行，便于恢复

对与相关行的节点，只删除上下节点对其的链接，保留对上下的链接，同样是为了便于恢复

void remove(int y) // 删除第y列和相关行
{
    r[l[y]] = r[y], l[r[y]] = l[y];
    for (int i = d[y]; i != y; i = d[i])
        for (int j = r[i]; j != i; j = r[j])
            d[u[j]] = d[j], u[d[j]] = u[j], s[col[j]]--;
}

恢复

即恢复所选列y，和所有的列y为1的行

由于保留了哨兵y的左右指针，所以恢复左右哨兵对哨兵y的链接

y列并未删除，可以通过y列到达相关行，相关行的节点也都保留了对上下节点的链接，从而恢复上下节点对相关行上的节点的链接即可。

void resume(int y) // 恢复第y列和相关行
{
    r[l[y]] = l[r[y]] = y;
    for (int i = d[y]; i != y; i = d[i])
        for (int j = r[i]; j != i; j = r[j])
            d[u[j]] = u[d[j]] = j, s[col[j]]++;
}

跳舞

跳舞操作就是我们递归和回溯的操作

如果当前矩阵删完了，那么输出可行解
否则，选择1最少的列y，删除y列，枚举行：
- 枚举行i，删除i的所有列，然后进行下一层跳舞
  - 跳舞成功，那么返回true
  - 跳舞失败，恢复第i行和所有列
恢复第y列，返回false

bool dance(int dep)
{
    if (!r[0])
    {
        for (int i = 0; i < dep; i++)
            cout << ans[i] << " ";
        return true;
    }
    int y = r[0];
    for (int i = r[0]; i; i = r[i])
        if (s[i] < s[y])
            y = i;

    remove(y);
    for (int i = d[y]; i != y; i = d[i])
    {
        ans[dep] = row[i];
        for (int j = r[i]; j != i; j = r[j])
            remove(col[j]);
        if (dance(dep + 1))
            return true;
        for (int j = r[i]; j != i; j = r[j])
            resume(col[j]);
    }
    resume(y);
    return false;
}

OJ练习

舞蹈链模板

P4929 【模板】舞蹈链（DLX） - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

板子题，直接跑板子即可

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
#define N 5505 // 1的节点数目+哨兵节点数目

int m, n, cnt = 0;                      // 行列，1节点编号
int u[N]{0}, d[N]{0}, l[N]{0}, r[N]{0}; // 四个方向的指针域
int row[N]{0}, col[N]{0};               // 每个节点的行号、列号
int h[505]{0};                          // 每一行的头节点
int s[505]{0};                          // 每一列1的个数
int ans[505]{0};                        // 选取的行

void init() // 初始化第0行哨兵节点
{
    for (int y = 0; y <= n; y++)
    {
        u[y] = d[y] = y;
        l[y] = y - 1, r[y] = y + 1;
    }
    l[0] = n, r[n] = 0;
    cnt = n;
}

void link(int x, int y) // i行j列插入点
{
    row[++cnt] = x, col[cnt] = y;
    s[y]++;
    u[cnt] = u[y];
    d[u[y]] = cnt;
    d[cnt] = y;
    u[y] = cnt;
    if (!h[x])
        h[x] = l[cnt] = r[cnt] = cnt;
    else
    {
        l[cnt] = l[h[x]];
        r[l[h[x]]] = cnt;
        l[h[x]] = cnt;
        r[cnt] = h[x];
    }
}

void remove(int y) // 删除第y列和关联行
{
    r[l[y]] = r[y], l[r[y]] = l[y];
    for (int i = d[y]; i != y; i = d[i])
        for (int j = r[i]; j != i; j = r[j])
            u[d[j]] = u[j], d[u[j]] = d[j], s[col[j]]--;
}

void resume(int y) // 恢复第y列和关联行
{
    r[l[y]] = l[r[y]] = y;
    for (int i = d[y]; i != y; i = d[i])
        for (int j = r[i]; j != i; j = r[j])
            u[d[j]] = d[u[j]] = j, s[col[j]]++;
}

bool dance(int dep) // 一同起舞吧！
{
    if (!r[0])
    {
        for (int i = 0; i < dep; i++)
            cout << ans[i] << " ";
        return true;
    }

    int y = r[0];
    for (int i = r[0]; i; i = r[i])
        if (s[i] < s[y])
            y = i;

    remove(y);
    for (int i = d[y]; i != y; i = d[i]) // 枚举选行
    {
        ans[dep] = row[i];
        for (int j = r[i]; i != j; j = r[j])
            remove(col[j]);
        if (dance(dep + 1))
            return true;
        for (int j = r[i]; i != j; j = r[j])
            resume(col[j]);
    }
    resume(y);
    return false;
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(nullptr), cout.tie(nullptr);
    //freopen("in.txt", "r", stdin);
    //freopen("out.txt", "w", stdout);
    
    cin >> m >> n;
    init();
    int t;
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
        {
            cin >> t;
            if (t)
                link(i, j);
        }
    if (!dance(0))
        cout << "No Solution!";
    return 0;
}

解数独

P1784 数独 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

数独问题是经典的精确覆盖问题。

那么如何抽象数独问题为舞蹈链能够解决的问题呢？

我们数独填满后要保证：

每一个格子都有数，81个格子即81种情况

每一行都有数，9个格子每个格子9种填法，所以81种情况

每一列都有数，类似地，也有81种情况

每一宫都有数，类似地，也有81种情况

这四个条件可以作为列，我们要让每个列精确覆盖，四个条件每个条件有81种情况一共是324列。

那么行就是我们可以填的所有情况，81个格子每一个格子有9种情况一共是729种情况。

所以就是在729 * 324的矩阵上跑DLX板子即可

注意链接时坐标的换算。

代码如下：

#include <iostream>
#include <cstring>
#include <vector>
#include <string>
#include <algorithm>
#include <set>
#include <unordered_map>
#include <climits>

using namespace std;
#define N 237000
int m = 729, n = 324, cnt = 0;          // 行列，点编号
int u[N]{0}, d[N]{0}, l[N]{0}, r[N]{0}; // 上下左右指针域
int row[N], col[N];                     // 行号，列号
int h[730]{0};                          // 行头节点
int s[325]{0};                          // 列节点数
int ans[82];                            // 选择的行
int g[9][9];                            // 矩阵
void init()
{
    for (int y = 0; y <= n; y++)
    {
        u[y] = d[y] = y;
        l[y] = y - 1, r[y] = y + 1;
    }
    l[0] = n, r[n] = 0;
    cnt = n;
}

void link(int x, int y) // x行y列插入点
{
    row[++cnt] = x, col[cnt] = y; // 记录行号列号
    s[y]++;                       // y列点+1
    u[cnt] = u[y], d[u[y]] = cnt;
    d[cnt] = y, u[y] = cnt; // 列尾插
    // 行尾插
    if (!h[x])
        h[x] = r[cnt] = l[cnt] = cnt;
    else
    {
        l[cnt] = l[h[x]], r[l[h[x]]] = cnt;
        r[cnt] = h[x], l[h[x]] = cnt;
    }
}

void remove(int y) // 删除第y列和相关行
{
    r[l[y]] = r[y], l[r[y]] = l[y];
    for (int i = d[y]; i != y; i = d[i])
        for (int j = r[i]; j != i; j = r[j])
            d[u[j]] = d[j], u[d[j]] = u[j], s[col[j]]--;
}

void resume(int y) // 恢复第y列和相关行
{
    r[l[y]] = l[r[y]] = y;
    for (int i = d[y]; i != y; i = d[i])
        for (int j = r[i]; j != i; j = r[j])
            d[u[j]] = u[d[j]] = j, s[col[j]]++;
}

bool dance(int dep)
{
    if (!r[0])
    {
        for (int i = 0, x, y, v; i < dep; i++)
        {
            x = (ans[i] - 1) / 9 / 9;
            y = (ans[i] - 1) / 9 % 9;
            v = ans[i] % 9;
            g[x][y] = v ? v : 9;
        }
        for (int i = 0; i < 9; i++)
        {
            for (int j = 0; j < 9; j++)
                cout << g[i][j] << " ";
            cout << '\n';
        }
        return true;
    }
    int y = r[0];
    for (int i = r[0]; i; i = r[i])
        if (s[i] < s[y])
            y = i;

    remove(y);
    for (int i = d[y]; i != y; i = d[i])
    {
        ans[dep] = row[i];
        for (int j = r[i]; j != i; j = r[j])
            remove(col[j]);
        if (dance(dep + 1))
            return true;
        for (int j = r[i]; j != i; j = r[j])
            resume(col[j]);
    }
    resume(y);
    return false;
}

signed main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    init();
    for (int i = 0, t; i < 9; i++)
        for (int j = 0; j < 9; j++)
        {
            cin >> t, g[i][j] = t;
            for (int k = 1; k <= 9; k++)
            {
                if (!t || t == k)
                {
                    int r = i * 81 + j * 9 + k;
                    link(r, i * 9 + j + 1);
                    link(r, 81 + i * 9 + k);
                    link(r, 81 * 2 + j * 9 + k);
                    link(r, 81 * 3 + (i / 3 * 3 + j / 3) * 9 + k);
                }
            }
        }
    dance(0);
    return 0;
}

N皇后

P1784 数独 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

N皇后问题是回溯法的经典问题，我们同样可以将其抽象为精确覆盖问题。

先确定限制条件：

每列有一个
每行有一个
主/副对角线最多有一个

所有情况：

每行可以有n列进行选择，所以有n * n种情况

那么我们限制列有6n - 2行，实际上我们只需要精确覆盖前n列，因为后4n - 2列无需精确覆盖，当前n列精确覆盖时，前2 n列必然精确覆盖，这是由规则决定我们链接特点从而决定了最终解的特点

然后跑板子即可。

#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
using namespace std;
#define N 13000 // t * t * (6 * t - 2)
int t;
long long sum = 0; // 方案总数

int n, m, cnt;                              // 长，宽，点的数量
int l[N], r[N], u[N], d[N], row[N], col[N]; // 每个点的左，右，上下，行，列信息
int h[170];                                 // 每行的头结点
int s[80];                                  // 每列的结点数
vector<int> ans(170);                       // 选择的行
auto cmp = [](const vector<int> &x, const vector<int> &y) -> bool
{
    int i = 0;
    while (x[i] == y[i] && i < t)
        i++;
    return x[i] < y[i];
};
vector<vector<int>> paths;
void init(int _n, int _m)
{
    m = _m, n = _n;

    for (int i = 0; i <= n; i++)
    {
        r[i] = i + 1;
        l[i] = i - 1;
        u[i] = d[i] = i;
    }
    r[n] = 0, l[0] = n;
    cnt = n;
}
void link(int x, int y) // x行y列插入点
{
    row[++cnt] = x, col[cnt] = y; // 记录行号列号
    s[y]++;                       // y列点+1
    u[cnt] = u[y], d[u[y]] = cnt;
    d[cnt] = y, u[y] = cnt; // 列尾插
    // 行尾插
    if (!h[x])
        h[x] = r[cnt] = l[cnt] = cnt;
    else
    {
        l[cnt] = l[h[x]], r[l[h[x]]] = cnt;
        r[cnt] = h[x], l[h[x]] = cnt;
    }
}
void remove(int y) // 删除第y列和相关行
{
    r[l[y]] = r[y], l[r[y]] = l[y];
    for (int i = d[y]; i != y; i = d[i])
        for (int j = r[i]; j != i; j = r[j])
            d[u[j]] = d[j], u[d[j]] = u[j], s[col[j]]--;
}
void resume(int y) // 恢复第y列和相关行
{
    r[l[y]] = l[r[y]] = y;
    for (int i = d[y]; i != y; i = d[i])
        for (int j = r[i]; j != i; j = r[j])
            d[u[j]] = u[d[j]] = j, s[col[j]]++;
}
void dance(int dep)
{
    if (r[0] > t)
    {
        sum++;
        vector<int> v(t + 1);
        for (int i = 0; i < dep; i++)
        {
            int x = ans[i] % t, y = (ans[i] - 1) / t + 1;
            if (x == 0)
                x = t;
            v[x] = y;
        }
        paths.emplace_back(v);

        return;
    }
    int y = r[0];
    for (int i = r[0]; i <= t; i = r[i])
        if (s[i] < s[y])
            y = i;

    remove(y);
    for (int i = d[y]; i != y; i = d[i])
    {
        ans[dep] = row[i];

        for (int j = r[i]; j != i; j = r[j])
            remove(col[j]);
        dance(dep + 1);
        for (int j = r[i]; j != i; j = r[j])
            resume(col[j]);
    }
    resume(y);
}

int main()
{
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    //freopen("in.txt", "r", stdin);
    cin >> t;
    init(t * t, 6 * t - 2);
    int x;
    for (int i = 0; i < t; i++)
    {
        for (int j = 0; j < t; j++)
        {
            link(i * t + j + 1, i + 1);
            link(i * t + j + 1, t + j + 1);
            link(i * t + j + 1, j - i + 3 * t);
            link(i * t + j + 1, i + j + 4 * t);
        }
    }
    dance(0);
    sort(paths.begin(), paths.end(), cmp);
    for (int k = 0; k < 3; k++)
    {
        for (int i = 1; i <= t; i++)
            cout << paths[k][i] << " ";
        cout << '\n';
    }

    cout << sum;
    return 0;
}