初次学习舞蹈链Dancing Links

最新推荐文章于 2024-01-11 00:14:02 发布

P1n9

最新推荐文章于 2024-01-11 00:14:02 发布

阅读量657

点赞数

分类专栏： # ACM__跳舞链

ACM__跳舞链专栏收录该内容

9 篇文章 0 订阅

订阅专栏

介绍几个讲的比较好的博客：
这篇博客容易理解，可以先看：
http://www.cnblogs.com/grenet/p/3145800.html
这篇博客阐述的也好，而且有实例分析（也是转载自此文）：
https://blog.csdn.net/WhereIsHeroFrom/article/details/79220897?utm_source=copy

Dancing Links正是十字交叉双向循环链表。
一、十字交叉双向循环链表
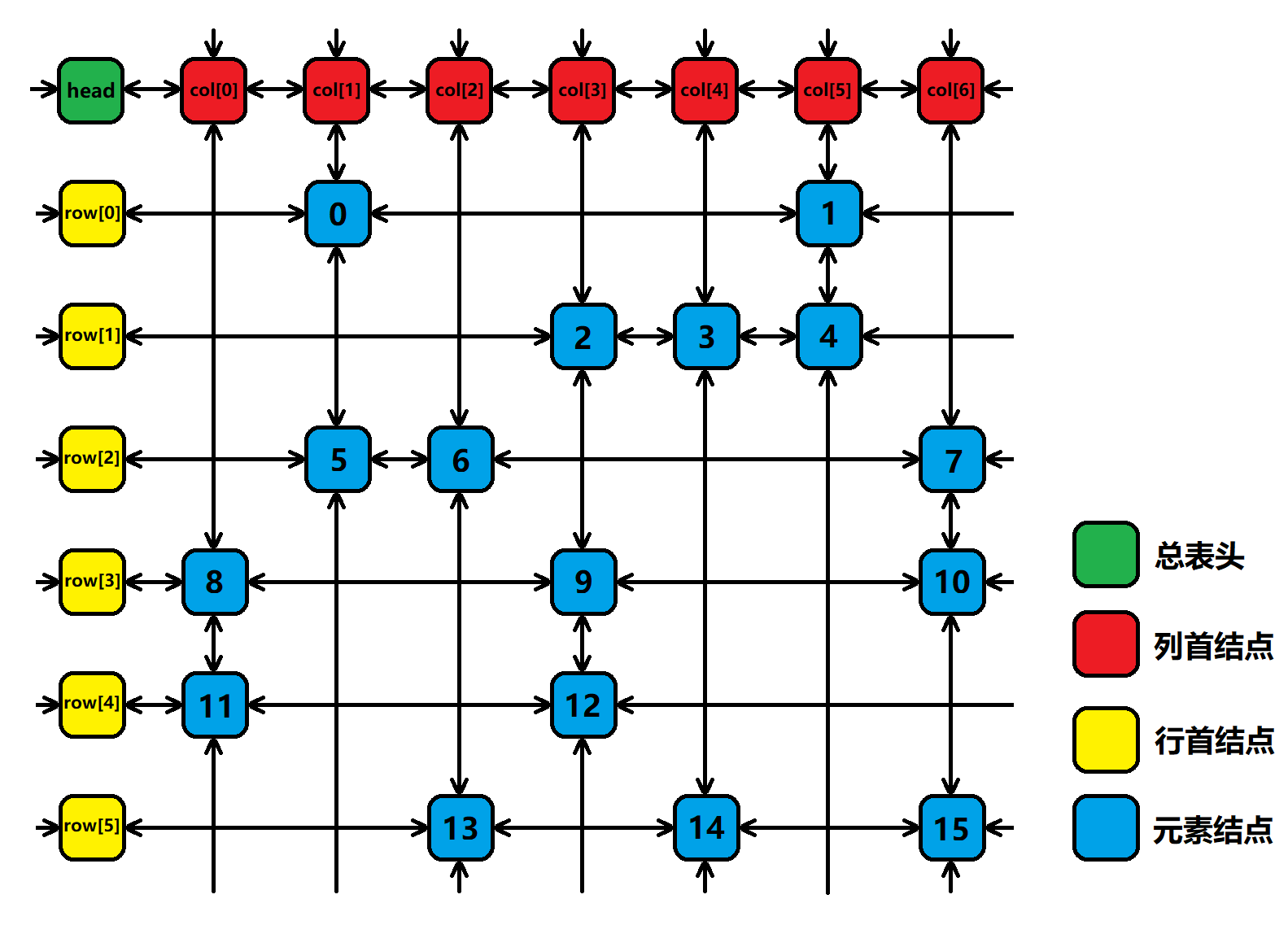
这种链表结构的每个结点有两类数据，分别为指针域和数据域。指针域为left、right、up、down，分别指向左、右、上、下四个其它结点；数据域则存储一些信息，比如这个结点对应于原始矩阵的行编号rowIdx，列编号colIdx等等。
原始矩阵中值为“1”的位置对应了一个Dancing Links结点，“0”的位置不是我们需要关心的。
那么接下来我们来看下，如何将一个矩阵转变为一个十字交叉双向循环链表。我们把Dancing Links结点分成以下四类：总表头head、列首结点col[]、行首结点row[]、元素结点node。
1) 总表头head：将列首结点col[]在水平方向串联起来，head->right指向矩阵的第一列的列首结点，head->left指向矩阵的最后一列的列首结点。特别的，当这个矩阵为空矩阵，也就是没有任何列时，head->right和head->left指向head本身，这也正是X算法的终止条件。
2) 列首结点col[]：令初始矩阵的列数为colCount，那么col[i]->right指向col[i+1]，特殊的，col[colCount-1]->right指向head；同理，col[0]->left指向head，其它的col[i]->left指向col[i-1]。col[i]->down和col[i]->up分别指向第i列的第一个“1”和最后一个“1”对应的结点，当col[i]的up和down都指向本身说明这列全是0；
3) 行首结点row[]：令初始矩阵的行数为rowCount，那么row[i]->up和row[i]->down都是无用指针，直接指向自己即可；row[i]->right和row[i]->left分别指向第i行的第一个“1”和最后一个“1”对应的结点。
4) 元素结点node：矩阵中“1”对应的结点，up、down指向其它node或列首结点；left、right指向其它node或行首结点。
如图三-5-1表示了之前的那个矩阵的十字交叉双向循环链表的数据结构表示。所有箭头的左右边界循环相连（上下边界亦循环相连）。每个元素结点代表了原矩阵中的那个“1”，即图中的蓝色方块，其中的数字代表对应内存池中的编号。初始化时，所有的行首结点的左右指针和列首结点的上下指针都指向自己，然后对矩阵进行行、列分别递增的顺序进行读取，读到“1”就执行结点插入操作，这正对应了图中蓝色结点的递增序。别以为这是飞行棋…
在这里插入图片描述

二、额外结点的意义
我们发现，图三-5-1中，除了蓝色结点，其它三种结点都是额外的，那么为什么要引入额外结点呢？
列首结点、行首结点都是存在既有数组中的，所以进行插入操作的时候可以达到O(1)，试想如果只有列首结点没有行首结点，那么插入一个处于(r, c)位置的结点时，c可以定位到列首结点col[c]，在进行对应行的插入时只能遍历竖向链表，插入的时间复杂度就变成O®了；同样，如果只有行首结点没有列首结点，那么插入复杂度就是O©的。
列首结点还有一个作用是区分不存在的列和全“0”的列。如果列c在搜索过程中被删除，那么列c的列首结点不会出现在链表结构中；而一个全“0”的列c，列首结点会在链表结构中，并且它的上下指针都指向自己。
总表头head主要还是为了空矩阵而存在的，试想如果一个矩阵为空，那么势必它的所有列首结点都没有了，那用什么来表示空矩阵呢？引入总表头后，只要总表头的左右指针都指向自己，就代表这是一个空矩阵。

三、Dancing Links X算法的具体实现
1、结点定义DLXNode
四类结点都定义为DLXNode，并且除了left、right、up、down四个指针数据外，还需要一些额外信息记录：
1）对于总表头，不需要额外记录信息；
2）对于列首结点，需要记录列编号colIdx，该列的结点个数colSum；
3）对于行首结点，需要记录行编号rowIdx；
4）对于元素结点，需要记录行编号rowIdx，列首指针colhead；

/*
DLXNode
 left, right        十字交叉双向循环链表的左右指针
 up, down           十字交叉双向循环链表的上下指针
 <用于列首结点>
 colSum             列的结点总数
 colIdx             列的编号
  
 <用于行首结点/元素结点>
 colHead            指向列首结点的指针
 rowIdx             DLXNode结点在原矩阵中的行标号
*/
class DLXNode {
public:
     DLXNode *left, *right, *up, *down;
    union {
         struct {
              DLXNode *colHead;   
             int rowIdx;
         }node;
        struct {
             int colIdx;
             int colSum;
        }col;
    }data;
};

2、链表定义DLX
十字交叉双向循环链表对于整个搜索来说，只有一个对象，所以这里采用单例实现。因为结点个数可能很多，所以可以将结点内存放在堆上避免栈溢出，row和col分别代表行首和列首结点，dlx_pool则为元素结点的对象池。可以在构造函数中利用new生成这些动态结点，在析构函数中delete。

/*
DLX （单例）
 head               head 只有左右（left、right）两个指针有效，指向列首
 rowCount, colCount 本次样例矩阵的规模（行列数）
 row[]              行首结点列表
 col[]              列首结点列表
 
 dlx_pool           结点对象池（配合dlx_pool_idx取对象）
*/
class DLX {
	 DLXNode *head;             // 总表头
 	int rowCount, colCount;    // 本次样例矩阵的规模（行列数） 
	 DLXNode *row, *col;        // 行首结点列表 / 列首结点列表
 
	 DLXNode *dlx_pool;         // 结点对象池
	 int dlx_pool_idx;              // 结点对象池下标
};
 dlx_pool = new DLXNode[MAXR*MAXC];
 col = new DLXNode[MAXC+1];
 row = new DLXNode[MAXR];

3、初始化
1)设置本次问题的规模总行数rowCount，总列数colCount，结点对象池下标dlx_pool_idx置零；
2)初始化列首结点，将总表头head和col[i]在水平方向用left和right指针串联起来，col[i]的up和down指针指向自己，代表这列在矩阵中均为“0”；对于每个列首结点col[i]，将其列编号置为i，列结点总数colSum置零；
3)初始化行首结点，将行首结点row[i]的四个指针都指向自己，将其行编号rowIdx置为i，对应列首结点的指针置NULL；
4、结点插入
按行递增、列递增的方式枚举R×C的矩阵A，如果第r行第c列的值A[r][c] = 1，则插入一个(r, c)的结点：
1)取出结点对象池中的一个结点Node（注意需要返回指针或者引用）；
2)取列首结点col[c]，将它设置为Node的列首结点，并且将Node插入到col[c]和col[c]->up之间，将col[c]的结点总数colSum自增1；
3)取行首结点row[r]，将Node的行编号rowIdx设置为r，并且将Node插入到row[r]和row[r]->left之间；
5、删列
删除列c包含两步：
1)移除列首结点col[c]，这里的移除指只移除水平方向，竖直方向不作任何修改；
2)从列首结点col[c]往下枚举，将每个元素结点对应的行进行移除（即删行）；
6、删行
删除行r的操作只需要修改row[r]上所有元素结点的up和down指针，只移除竖直方向，水平方向不作任何修改；
7、开始跳舞
X算法的主体，具体步骤之前已经描述过，现直接给出深度优先搜索的实现如下：

bool DLX::dance(int depth) {
 	// 当前矩阵为空，说明找到一个可行解，算法终止 
 	if(isEmpty()) {
  		resultCount = depth;
 	 	return true;
	 }
 	DLXNode *minPtr = get_min_col();
	 // 删除minPtr指向的列 
	 cover(minPtr);
	 // minPtr为结点数最少的列，枚举这列上所有的行
	 for(DLXNode *p = minPtr->down; p != minPtr; p = p->down) {
 		 // 令r = p->getRowIdx()，行r放入当前解 
  		result[depth] = p->getRowIdx();
  		// 行r上的结点对应的列进行删除 
  		for(DLXNode *q = p->right; q != p; q = q->right) {
  			 cover(q->getColHead());
  		}
 		 // 进入搜索树的下一层 
  		if(dance(depth+1, maxDepth)) {
 		  	return true;
  		}
 		 // 行r上的结点对应的列进行恢复 
 		 for(DLXNode *q = p->left; q != p; q = q->left) {
 		  	uncover(q->getColHead());
	  	}
 	}
 	// 恢复minPtr指向的列
	 uncover(minPtr); 
	 return false;
}

上面是转载的博客里对Dancing Links算法的介绍

然后是重复覆盖：
1、重复覆盖的定义
【例题9】给定一个R×C（R, C <= 50）的01矩阵，问是否存在这样一个行集合，使得集合中每一列至少一个“1”。
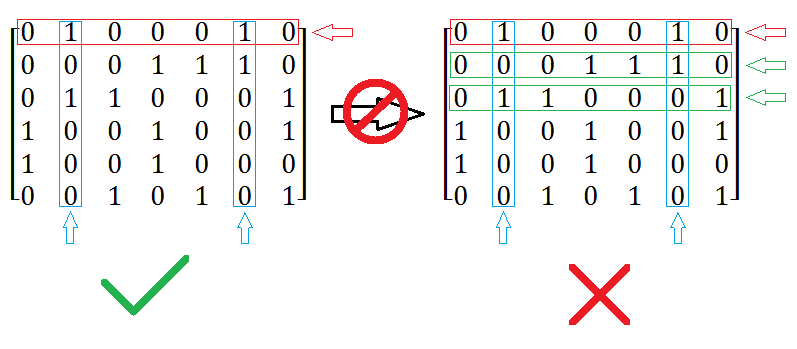
重复覆盖是精确覆盖的一般情况，限制条件远远没有精确覆盖强。回忆一下X的算法思路，我们发现重复覆盖可以参照精确覆盖的方法构建Dancing Links链表，然后枚举行的选取，进而删除该行上有“1”的列，但是仅此而已，无法再删除列对应的行。如图六-1-1所示，选择第一行（红色框），然后删除蓝色的列（试想一下，如果是精确覆盖，我们还可以删除绿色的行），然而重复覆盖无法删除绿色的行，这是因为选取的行集合允许在每列上有多个“1”，如果过多的删除有可能导致可行解的擦肩而过。
在这里插入图片描述

图六-1-1
这样带来的问题就是矩阵规模的下降速度会大大减慢，从而使得搜索的状态空间树十分庞大，这时候往往需要剪枝，在介绍剪枝之前，让我们先来看一个更加复杂的情况。

【例题10】给定一个R×C（R, C <= 50）的01矩阵，找出最少的行集合，使得集合中每一列至少一个“1”。

为了满足搜索的行数最小这个条件，我们需要引入迭代加深。

2、迭代加深（IDA*）

迭代加深，顾名思义，就是深度的迭代。即枚举一个最大深度，然后对问题进行搜索，搜索过程记录当前深度，如果当前深度大于最大深度则无条件返回。例如，假设枚举的最大深度为3，那么搜索选取01矩阵的行时最多只能选择3行，当深度大于3深搜函数必须返回。
那么可以枚举深度，然后再进行搜索。

3、启发式函数

引入最大深度的原因，除了能第一时间找到“最少”，更大程度上是便于启发性剪枝。考虑到当前枚举深度depth，最大枚举深度maxDepth，令K = ()。则在这种情况下，还有K步决策，或者说是只能再最多选择K行，那么如果我们能够设计一个估价函数H()，函数返回的是至少还需要多少行才能完成重复覆盖（这是个估计值，不是确定的）。并且H() > K，则代表当前搜索条件下，头已经不可能搜到可行解了，可以直接返回，使得搜索树的一些分支不需要再进行无谓的搜索，此所谓“剪枝”。

H()函数是一个估计值，并不能精确计算出来（如果能精确计算出来，那问题本身就可以直接用这个函数来计算了），并且这个估计值一定是要比实际值小的，即实际值 > 估计值H() > K。

H()函数原理：X算法的终止条件是列为空，那么我们现在要做的就是要模拟删除所有的列，这里说的删除并不是真正的删除，而是做一个标记。假设Dancing Links 的01矩阵的列数小于64，那么每一行可以压缩成一个INT64的整型（当然，如果列数大于64的话，可以压缩在一个INT64的数组里，总之目的就是利用位运算减少轮询操作），用R[i]表示第i行的那个64位整数。用一个全局标记X来记录剩下列的模拟删除情况（X的二进制第i位为“1”代表第i列已经被模拟删除）。

H()函数计算过程：任意找一个未被模拟删除的列c，计数器cnt+1，选中列c上有“1”的行r，令X = X or R[r]，依次往复直到不存在这样的列c。最后的计数器cnt就是那个估计值。

4、引用计数
重复覆盖的时候，每次选择一行，删除行上有“1”的列时，有可能会枚举到已经删除的列，如果已经删除则需要进行标记，但是不能标记为已经“删除”和“未删除”两种状态。因为除了删除，还需要恢复，所以删除的状态其实是有“被删除0次”、“被删除1次”、“被删除2次”、…“被删除N次”这样的多种状态组成的。
正确做法是用一个标记数组D[i]，标记第i列删除的次数。每次执行删除时，标记+1，并且判断标记为1才执行删除；每次执行恢复时，标记-1，并且判断标记为0时才执行恢复。

接下来也是从网上找的模板：

//最大行数
const int MN = 1005;
//最大列数
const int MM = 1005;
//最大点数
const int MNN = 1e5 + 5 + MM;

struct DLX
{
    //一共n行m列，s个节点
    int n,m,s;
    //交叉十字链表组成部分
    //第i个节点的上U下D左L右R，所在位置row行col列
    int U[MNN],D[MNN],L[MNN],R[MNN],row[MNN],col[MNN];
    //H数组记录行选择指针，S数组记录覆盖个数
    int H[MN],S[MM];
    //res记录行个数，ans数组记录可行解
    int res,ans[MN];
    //初始化空表
    void init(int x,int y)
    {
        n = x,m = y;
        //其中0节点作为head节点,其他作为列首节点
        for(int i = 0;i <= m;++i){
            U[i] = D[i] = i;
            L[i] = i - 1;
            R[i] = i + 1;
        }
        R[m] = 0;L[0] = m;
        s = m;
        memset(S,0,sizeof(S));
        memset(H,-1,sizeof(H));
    }
    void Insert(int r,int c)
    {
        //节点数加一，设置s节点所处位置，以及S列覆盖个数加一
        s++;row[s] = r;col[s] = c;S[c]++;
        //将s节点插入对应列中
        D[s] = D[c];U[D[c]] = s;
        U[s] = c;D[c] = s;
        if(H[r] < 0){//如果该行没有元素，H[r]标记该行起始节点
            H[r] = L[s] = R[s] = s;
        }else{
            //将该节点插入该行第一个节点后面
            R[s] = R[H[r]];
            L[R[H[r]]] = s;
            L[s] = H[r];
            R[H[r]] = s;
        }
    }
    //精确覆盖
    void Remove(int c)
    {
        //删除c列
        L[R[c]] = L[c];R[L[c]] = R[c];
        //删除该列上的元素对应的行
        for(int i = D[c];i != c;i = D[i]){//枚举该列元素
            for(int j = R[i];j != i;j = R[j]){//枚举列的某个元素所在行遍历
                U[D[j]] = U[j];
                D[U[j]] = D[j];
                //将该列上的S数组减一
                --S[col[j]];
            }
        }
    }
    void resume(int c)
    {
        //恢复c列
        for(int i = U[c];i != c;i = U[i]){//枚举该列元素
            for(int j = L[i];j != i;j = L[j]){
                U[D[j]] = j;D[U[j]] = j;
                ++S[col[j]];
            }
        }
        L[R[c]] = c;R[L[c]] = c;
    }
    bool dance(int deep)
    {
        if(res < deep) return false;
        //当矩阵为空时,说明找到一个可行解，算法终止
        if(R[0] == 0){
            res = min(res,deep);
            return true;
        }
        //找到节点数最少的列，枚举这列上的所有行
        int c = R[0];
        for(int i = R[0];i != 0;i = R[i]){
            if(S[i] < S[c]){
                c = i;
            }
        }
        //删除节点数最少的列
        Remove(c);
        for(int i = D[c];i != c;i = D[i]){
            //将行r放入当前解
            ans[deep] = row[i];
            //行上节点对应的列上进行删除
            for(int j = R[i];j != i;j = R[j])
                Remove(col[j]);
            //进入下一层
            dance(deep + 1);
            //对行上的节点对应的列进行恢复
            for(int j = L[i];j != i;j = L[j])
                resume(col[j]);
        }
        //恢复节点数最少列
        resume(c);
        return false;
    }

    //重复覆盖
    //将列与矩阵完全分开
    void Remove1(int c)
    {
        for(int i = D[c];i != c;i = D[i]){
            L[R[i]] = L[i];
            R[L[i]] = R[i];
        }
    }
    void resume1(int c)
    {
        for(int i = D[c];i != c;i = D[i]){
            L[R[i]] = R[L[i]] = i;
        }
    }
    int vis[MNN];
    //估价函数，模拟删除列，H()，函数返回的是至少还需要多少行才能完成重复覆盖
    int A()
    {
        int dis = 0;
        for(int i = R[0];i != 0;i = R[i]) vis[i] = 0;
        for(int i = R[0];i != 0;i = R[i]){
            if(!vis[i]){
                dis++;vis[i] = 1;
                for(int j = D[i];j != i;j = D[j]){
                    for(int k = R[j];k != j;k = R[k]){
                        vis[col[k]] = 1;
                    }
                }
            }
        }
        return dis;
    }

    void dfs(int deep)
    {
        if(!R[0]){
            //cout << res << endl;
            res = min(res,deep);
            return ;
        }
        if(deep + A() >= res) return ;
        int c = R[0];
        for(int i = R[0];i != 0;i = R[i]){
            if(S[i] < S[c]){
                c = i;
            }
        }
        for(int i = D[c];i != c;i = D[i]){
            //每次将第i列其他节点删除，只保留第i节点，为了找该行的节点
            Remove1(i);
            //将列上的节点完全与矩阵脱离，只删列首节点是不行的
            for(int j = R[i];j != i;j = R[j]){
                Remove1(j);
            }
            dfs(deep + 1);
            for(int j = L[i];j != i;j = L[j]){
                resume1(j);
            }
            resume1(i);
        }
    }
}dlx;

P1n9

关注

0
点赞
踩
6

收藏

觉得还不错? 一键收藏
0
评论
初次学习舞蹈链Dancing Links

介绍几个讲的比较好的博客：这篇博客容易理解，可以先看：http://www.cnblogs.com/grenet/p/3145800.html这篇博客阐述的也好，而且有实例分析（也是转载自此文）：https://blog.csdn.net/WhereIsHeroFrom/article/details/79220897?utm_source=copyDancing Links正是十字交叉...
复制链接

扫一扫