统计计算学习【随机模拟_Chapter4模拟随机变量-4.1逆变换法】

补充：伪随机数&线性同余方法产生随机数

1. 伪随机数的概念：
   

2. 线性同余法（LCG方法）----产生均匀随机数【《统计计算》高惠璇】

• 同余的概念：
  
• LCG方法的递推公式：
  
• 例子：
  
• 周期的概念：
  

Chapter4 模拟随机变量

4.1 逆变换方法

4.1.1 离散型随机变量情形

特殊：

4.1.1.1 例子：

例4.1 产生给定概率分布的随机变量X

#方法1：
X <- 1:4 
p <- c(0.01,0.05,0.40,0.45)
sample(X,5,prob=p,replace=TRUE)

#方法2：
n <- 5
X <- rep(0,n);X
for(i in 1:n){
  u <- runif(1)
  if(u < 0.15) X[i] = 1
  else if(u < 0.15) X[i] = 2
  else if(u < 0.55) X[i] = 3
  else X[i] = 4
}
X

例4.2 随机排列1,…,n / 置换

#方法2的算法实现
perm <- function(n){
  X=1:n
  k=n
  while(k > 1){
    u <-  runif(1)
    I <- floor(k * u) + 1
    #引入中间变量V
    V <- X[k]
    X[k] <- X[I]
    X[I] <- V
    k <- k-1
  }
  X
}
#调用 perm()函数
perm(10)

例4.3 几何随机变量的生成

#例4.3 几何随机变量的生成
#产生n个参数为p的几何随机变量X的算法实现
n <- 8
U <- runif(n)
X <- floor(log(U) / log(1-p)) + 1
X

例4.4 产生带有均值 $\lambda$的Poisson随机变量

#用递归算法计算Poisson分布的概率程序：
lambda <- 3
r <- 6
k <- 8
n <- 8
p <- numeric(k)
p[1] <- exp(-lambda)
for(n in 2:r){
  p[n] <- exp(-lambda)
  for(j in 0:(n-2)){
    p[n] <- p[n] * lambda / (j + 1)
  }
  p[n]
}

感觉下面的代码哪一步出错了

#产生带有均值lambda的Poisson随机变量的逆变换算法
rpois <- function(n,lambda){
    Y <- rep(0,n)   #注意：课本这里写错了，把这行代码写进了for循环里，以至于结果不对
    for(j in 1:n){
       u <- runif(1)
       i <- 0;p <- exp(-lambda);F <- p
    
       while(u >= F){
          p <- lambda * p / (i + 1);F <- F + p;i <- i + 1
       }
       Y[j] <- i
    }
  Y
}
#调用rpois()函数
rpois(5,7)

例4.5 产生二项随机变量

#例4.5二项随机变量
#产生m个参数为(n,p)的二项随机变量的代码：
rb <- function(m,n,p){
  Y <- rep(0,m)
  for(j in 1:m){
    c <- p / (1-p);i <- 0;pr <- (1-p)^n;F <- pr
    u <- runif(1)
    while(u > F){
      pr <- c * (n - i)*pr / (i + 1);F <- F + pr;i <- i + 1 
    }
      Y[j] <- i
  }
  Y
}
rb(8,6,0.4)

例4.6 产生多项分布的随机数

较复杂，懂算法即可，代码不要求掌握

下面这段代码有点不大懂

#例4.6 多项分布
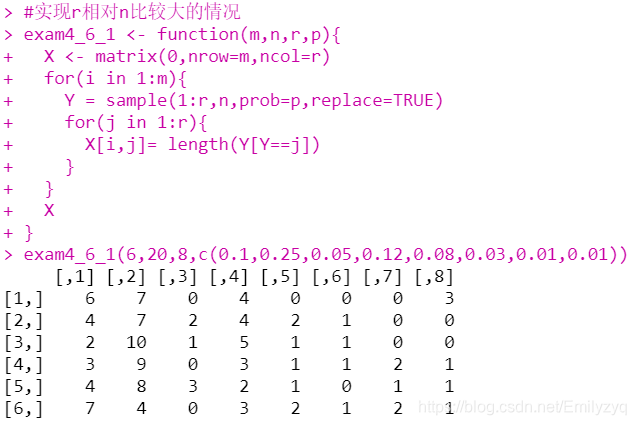
#实现r相对n比较大的情况
exam4_6_1 <- function(m,n,r,p){
  X <- matrix(0,nrow=m,ncol=r)
  for(i in 1:m){
    Y = sample(1:r,n,prob=p,replace=TRUE)
    for(j in 1:r){
      X[i,j]= length(Y[Y==j])
    }
  }
  X
}
exam4_6_1(6,20,8,c(0.1,0.25,0.05,0.12,0.08,0.03,0.01,0.01))

4.1.2 连续性随机变量情形

【后续补上】