[HNOI2016] 序列（线段树 + 莫队 + 倍增）

problem

luogu-P3246

心路历程+卡常历程+问题存疑

一直在想莫队的做法。发现左右指针的移动对应一段左/右端点固定的子序列，然后可以一个数代表一段相同的贡献。

就开始求 $ls{t}_i,nx{t}_i$ 了。

仔细想想需要找到 $ls{t}_{ls{t}_i}<l\le ls{t}_i$ 的特殊位置，然后要知道这中间点的贡献。

我就在来了个线段树维护区间和，然后用 $\text{set}$ 存 $ls{t}_i$ 二分找。

后来半天过不了样例，不是过大就是过小。

隐约间觉得不对劲，后来真的好像不对劲，我就大刀阔斧直接砍了。

开始怀疑自己的莫队算法。此时经过了八点半到九点十分共四十多分钟的时间。

我开始尝试整体二分，后面发现自己完全不会分治。此时我陷入了困境。

我又倒回去想了下莫队，我发现问题出在 $ls{t}_i$ 中间不是所有点都是对应在 $[l,r]$ 的贡献，我好像算多了。

因为 $ls{t}_i$ 是从 $i$ 出发得到的，而非整体的 $r$。

难道我只用维护一个全局的？不，这样会算少。

突然我意识到可以把这种关系建成树！并且发现了编号之间与子序列间的对应关系。

此时时间大概在酒店四五十左右，我就开始敲了。

过程比较顺利，十点半不到？就敲完了。然后开始调，输出中间结果，发现最后结果已经和样例快要吻合时，我就更加坚定了自己的做法。

十一点我通过了小样例，紧接着大样例也是正确的。

但很遗憾，耗时 $3.6s$ 多。

我发现输入数据过多，就换成了快读快输。耗时变成了 $3.0s$ 多。

接着我觉得倍增对于极限数据也只会到 $16$ ，所以卡了下倍增的循环。耗时缩减为 $2.6s$。

改下块长加 $O2$ 就能看看卡过。

但是当时我尝试了一下用莫队的奇偶优化，时间瞬间到了 $1.9s$ 左右。

此时出现了个大问题！我发现这样就跑不过大样例了。

我对此非常疑惑。

下午又研究了一番，发现当我将莫队的四个指针移动前后两个交换位置，也会跑不过大样例？！！莫队询问排序块内按右端点降序排列也不行！

这下真给我整不会了，我突然猜是不是爆 long long 了，用 $\text{assert}$ 发现没有，自己算极限也是 $6e18$ 不到。

后面通过数据，我觉得应该是倍增到最后不能往上跳部分出现了问题。

但是这样怎么可能会让我的第一次建构代码跑过去呢？

至今我仍然不清楚。

只能说非常幸运的在第一次敲代码的时候就跑过去了把。

如果有人知道这是为什么的话，麻烦请联系一下我！谢谢了。

solution

由于昨天做的一道题题解提了一句莫队二次离线，形式就是 $l\le x\le y\le r$。

所以一看到这个题，我就在想莫队的做法。

莫队反正就是左端点分块排序，右端点块内递增，就两个指针移动的板子，时间复杂度就带了个 $\sqrt{n}$。

问题是如何快速计算移动 $l/r$ 一个位置后对应的答案动态变化。

以右移 $r$ 为例，当 $r\leftarrow r+1$的时候，我们需要新加 $[l,r]\sim r+1$ 共 $r-l+1$ 组新的子序列贡献。

然后发现，我们只需要跳较小值的位置即可。

具体而言，假设 $p$ 满足 $a_p\le a_{r+1}\wedge {\forall }_{p<i<r+1}{a}_i>a_{r+1}$。

最大的不超过 $a_{r+1}$ 的位置，记为 $ls{t}_{r+1}$。

则对于 $[p,r]\sim r+1$ 共 $r-p+1$ 组子序列的贡献都是 $a_p$。

同理我们找到 $ls{t}_p$，然后共 $p-ls{t}_p+1$ 组子序列的贡献都是 $a_{ls{t}_p}$。

以此类推$\dots$直到跳到 $<l$ 的位置，$l$ 开头那一段贡献可能不完整，简单处理一下即可。

我们肯定不能暴力跳，注意到一个数对应的完整区间贡献是固定的，所以我们可以倍增！

我们将 $ls{t}_i\to i$ 建立有向边，然后生成一棵树，不难发现。$(u-fa)\ast a_u$ 即为 $u$ 对应的完整贡献。

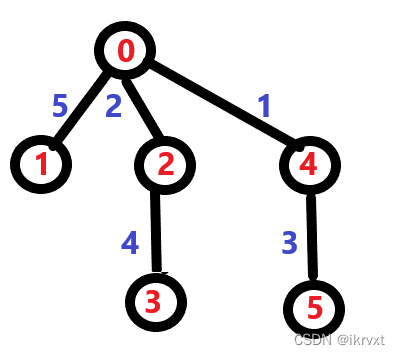
至于找 $ls{t}_i$，答主比较无脑，直接权值线段树上，完全不带脑子的大常数。而且 $a_i$ 值域过大，还加了个离散化。

$r$ 左移减去贡献与上面的过程完全一样。

而 $l$ 的左移右移则需要维护 $nx{t}_i$，最小的不大于 $a_i$ 的位置。获得方式同 $ls{t}_i$。

同样 $nx{t}_i\to i$ 建立有向边，生成一棵树。

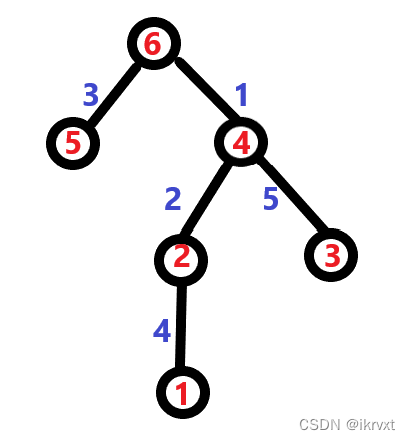
为了使得点与父节点之间能算出点的贡献，我们钦定找不到的 $ls{t}_i=0,nx{t}_i=n+1$。

时间复杂度大概是 $O(n\sqrt{n}\log n)$。

会被卡，那就稍微调整一下块长。

code

#include <bits/stdc++.h>
using namespace std;
#define lson now << 1
#define rson now << 1 | 1
#define mid  (l + r >> 1)
#define ll long long
#define maxn 100005
int n, Q, B; ll ans;
int a[maxn], b[maxn], block[maxn], lst[maxn], nxt[maxn];
ll ret[maxn];
struct query { int l, r, id; }q[maxn];

namespace MaxSgt {
	int Max[maxn << 2];
	void modify( int now, int l, int r, int p, int v ) {
		if( l == r ) { Max[now] = v; return; }
		if( p <= mid ) modify( lson, l, mid, p, v );
		else modify( rson, mid + 1, r, p, v );
		Max[now] = max( Max[lson], Max[rson] );
	}
	int query( int now, int l, int r, int L, int R ) {
		if( R < l or r < L ) return 0;
		if( L <= l and r <= R ) return Max[now];
		return max( query( lson, l, mid, L, R ), query( rson, mid + 1, r, L, R ) );
	}
}

namespace MinSgt {
	int Min[maxn << 2];
	void build( int now, int l, int r ) {
		Min[now] = n + 1;
		if( l == r ) return;
		build( lson, l, mid );
		build( rson, mid + 1, r );
	}
	void modify( int now, int l, int r, int p, int v ) {
		if( l == r ) { Min[now] = v; return; }
		if( p <= mid ) modify( lson, l, mid, p, v );
		else modify( rson, mid + 1, r, p, v );
		Min[now] = min( Min[lson], Min[rson] );
	}
	int query( int now, int l, int r, int L, int R ) {
		if( R < l or r < L ) return n + 1;
		if( L <= l and r <= R ) return Min[now];
		return min( query( lson, l, mid, L, R ), query( rson, mid + 1, r, L, R ) );
	}
}

struct tree {
	vector < int > G[maxn];
	int f[maxn][17]; ll g[maxn][17];
	void addedge( int u, int v ) {
		G[u].push_back( v );
	}
	int Fabs( int x ) {
		return x < 0 ? -x : x;
	}
	void dfs( int u, int fa ) {
		f[u][0] = fa, g[u][0] = 1ll * Fabs( u - fa ) * b[a[u]]; 
		for( int i = 1;i < 17;i ++ ) {
			f[u][i] = f[f[u][i - 1]][i - 1];
			g[u][i] = g[f[u][i - 1]][i - 1] + g[u][i - 1];
		}
		for( int i = 0;i < G[u].size();i ++ ) dfs( G[u][i], u );
	}
}L, R;

void AddR( int l, int r ) {
	for( int i = 16;~ i;i -- )
		if( L.f[r][i] >= l ) ans += L.g[r][i], r = L.f[r][i];
	ans += 1ll * (r - l + 1) * b[a[r]];
}

void SubR( int l, int r ) {
	for( int i = 16;~ i;i -- )
		if( L.f[r][i] >= l ) ans -= L.g[r][i], r = L.f[r][i];
	ans -= 1ll * (r - l + 1) * b[a[r]];
} 

void AddL( int l, int r ) {
	for( int i = 16;~ i;i -- )
		if( R.f[l][i] <= r ) ans += R.g[l][i], l = R.f[l][i];
	ans += 1ll * (r - l + 1) * b[a[l]];
}

void SubL( int l, int r ) {
	for( int i = 16;~ i;i -- )
		if( R.f[l][i] <= r ) ans -= R.g[l][i], l = R.f[l][i];
	ans -= 1ll * (r - l + 1) * b[a[l]];
}

void read( int &x ) {
	x = 0; int f = 1; char s = getchar();
	while( s < '0' or s > '9' ) {
		if( s == '-' ) f = -1; 
		s = getchar();
	}
	while( '0' <= s and s <= '9' ) {
		x = (x << 1) + (x << 3) + (s ^ 48);
		s = getchar();
	}
	x *= f;
}

void print( ll x ) {
	if( x < 0 ) putchar('-'), x = -x;
	if( x > 9 ) print( x / 10 );
	putchar( x % 10 + '0' );
}

int main() {
	read( n ), read( Q );
	B = 400;
	for( int i = 1;i <= n;i ++ ) read( a[i] );
	for( int i = 1;i <= Q;i ++ ) read( q[i].l ), read( q[i].r ), q[i].id = i;
	for( int i = 1;i <= n;i ++ ) block[i] = (i - 1) / B + 1;
	sort( q + 1, q + Q + 1, []( query x, query y ) { return (block[x.l] == block[y.l]) ? (x.r < y.r) : (x.l < y.l); } );
	for( int i = 1;i <= n;i ++ ) b[i] = a[i];
	sort( b + 1, b + n + 1 );
	int m = unique( b + 1, b + n + 1 ) - b - 1;
	for( int i = 1;i <= n;i ++ ) a[i] = lower_bound( b + 1, b + m + 1, a[i] ) - b;
	for( int i = 1;i <= n;i ++ ) {
		lst[i] = MaxSgt :: query( 1, 1, m, 1, a[i] );
		MaxSgt :: modify( 1, 1, m, a[i], i );
		L.addedge( lst[i], i );
	}
	MinSgt :: build( 1, 1, m );
	for( int i = n;i >= 1;i -- ) {
		nxt[i] = MinSgt :: query( 1, 1, m, 1, a[i] );
		MinSgt :: modify( 1, 1, m, a[i], i );
		R.addedge( nxt[i], i );
	}
	L.dfs( 0, 0 );
	R.dfs( n + 1, n + 1 );
	int curl = 1, curr = 0;
	for( int i = 1;i <= Q;i ++ ) {
		int l = q[i].l, r = q[i].r;
		while( curr < r ) AddR( curl, ++ curr );
		while( curr > r ) SubR( curl, curr -- );
		while( curl > l ) AddL( -- curl, curr );
		while( curl < l ) SubL( curl ++, curr );
		ret[q[i].id] = ans;
	}
	for( int i = 1;i <= Q;i ++ ) print( ret[i] ), putchar('\n');
	return 0;
}