（十）支撑向量机SVM

一，什么是支撑向量机

Support Vector Machine

既可以解决分类问题，也可以解决回归问题

当决策边界不唯一带来的问题就是不适定问题（典型是图像处理中的一些问题，比如马赛克，去噪，图像放大，图像修补等）

逻辑回归的决策边界为何是唯一的？

逻辑回归通过求使损失函数最小的参数求解，损失函数完全是由数据集决定的。某一个数据的影响可能就会使决策边界偏离真实的边界。进而降低了泛化能力。

SVM的决策边界不仅可以对数据样本进行划分，还希望对未来数据的泛化能力也很好。SVM的决策边界可以均衡俩个分类样本间的距离，让边界离分类样本都要尽可能的远。

解决的是线性可分问题

Hard Margin SVM 严格的

Soft Margin SVM

二，SVM背后的最优化问题

点到直线的距离公式：

拓展到n维空间：

假设n维空间中求得的决策边界满足：

那么所有的样本点满足（拆绝对值后）：

注意在这里样本点对应的标签改为了1和-1而不是1和0！

进一步除以分母

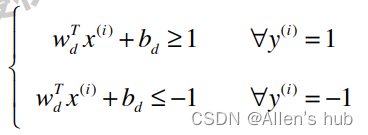
可以在图中表示出来：

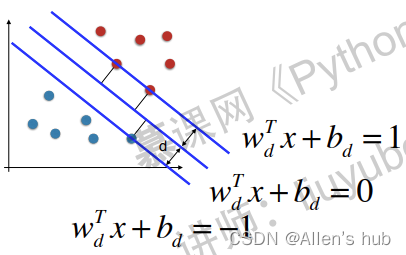
合并俩个不等式

对于任意的支撑向量X，我们要最大化：

但是由于对于支撑向量来说，代入分母恒为±1，因此化成最大化：

进一步改成：

最优化过程中的限定条件是：

变成平方方便求导。

最终的SVM问题就是求解带有条件的函数最值问题。

三，Soft Margin和SVM的正则化

线性的决策边界允许对训练样本有一定的容错率，进而提高对预测数据的泛化能力。

如果样本点张这样，那么使用线性的决策边界是无论如何不可能完成分类的。容错的SVM就是Soft Margin SVM。

回顾Hard Margin SVM的求解函数：

现在我们可以对他的条件适当的放松。

在图中就可以表示为：

其中的虚线部分就是：

表述就是：允许有样本点落在虚线和HMSVM的边界内。这样引入另一个参数。

我们的最优化目标就可以表示为：

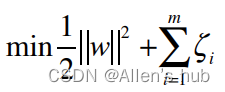
这样我们既可以有SVM的思想，又可以使得算法的容忍错误的程度又尽可能的小。后边那一项就是SVM的正则项。

在实际应用中，SVM和正则项的比例是不一定相同的，我们一般在正则项前加上超参数。

条件依旧是：

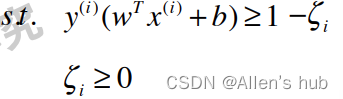
同样，正则化项也有对应的L1与L2正则：

四，scikit-learn中的SVM

和kNN一样，要做数据的标准化处理！

因为涉及距离！如果在每个维度上数据的量纲不同就会出现问题，因此要标准化处理。

导入数据：

import numpy as np

import matplotlib.pyplot as plt

from sklearn import datasets

from sklearn.preprocessing import StandardScaler

from sklearn.svm import LinearSVC

iris = datasets.load_iris()

X = iris.data

y = iris.target

X = X[y<2,:2] #取俩个类别

y = y[y<2]

plt.scatter(X[y==0,0], X[y==0,1], color='red')

plt.scatter(X[y==1,0], X[y==1,1], color='blue')

plt.show()

标准化：

standardScaler = StandardScaler()

standardScaler.fit(X)

X_standard = standardScaler.transform(X)

使用线性SVM：

svc = LinearSVC(C=1e9) #这里的C在SVM前，C越大，容错程度越小，偏向HardMargin

svc.fit(X_standard, y)

使用绘制决策边界的函数并绘制：

plot_decision_boundary(svc, axis=[-3, 3, -3, 3])

plt.scatter(X_standard[y==0,0], X_standard[y==0,1])

plt.scatter(X_standard[y==1,0], X_standard[y==1,1])

plt.show()

svc2 = LinearSVC(C=0.01) #改变权重

svc2.fit(X_standard, y)

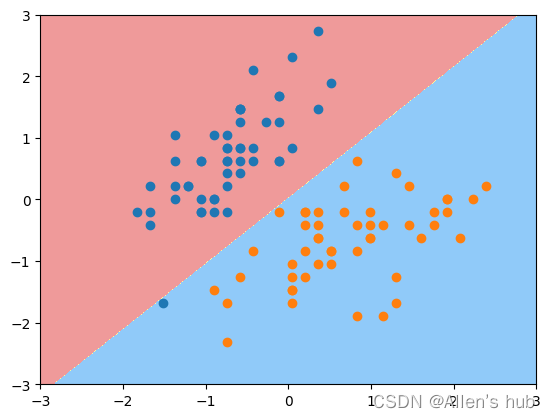
利用svc.coef_和svc.intercept_查看系数和截距

定义绘制SVM的边界函数：

绘制HardMargin的决策边界

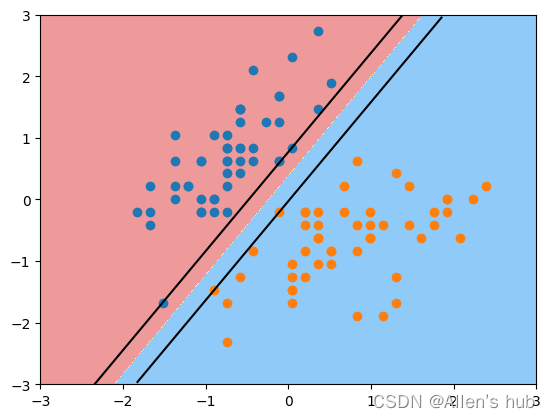
对于svc2的决策边界：

五，SVM中使用多项式特征和核函数

自定义多项式特征：

数据导入：

import numpy as np

import matplotlib.pyplot as plt

from sklearn import datasets

from sklearn.preprocessing import PolynomialFeatures, StandardScaler

from sklearn.svm import LinearSVC

from sklearn.pipeline import Pipeline

def PolynomialSVC(degree, C=1.0): #创建管道，默认C是1.0

    return Pipeline([

        ("poly", PolynomialFeatures(degree=degree)), #加入多项式特征

        ("std_scaler", StandardScaler()),

        ("linearSVC", LinearSVC(C=C)) #C传入用户定义的C

    ])

X, y = datasets.make_moons() #自动生成的非线性数据

plt.scatter(X[y==0,0], X[y==0,1])

plt.scatter(X[y==1,0], X[y==1,1])

plt.show()

X, y = datasets.make_moons(noise=0.15, random_state=666) #加入噪音

使用多项式特征的SVM：

poly_svc = PolynomialSVC(degree=3)

poly_svc.fit(X, y)

使用上节定义的边界绘图函数：

plot_decision_boundary(poly_svc, axis=[-1.5, 2.5, -1.0, 1.5])

plt.scatter(X[y==0,0], X[y==0,1])

plt.scatter(X[y==1,0], X[y==1,1])

plt.show()

使用多项式核函数的SVM：

from sklearn.svm import SVC

def PolynomialKernelSVC(degree, C=1.0):

    return Pipeline([

        ("std_scaler", StandardScaler()),

        ("kernelSVC", SVC(kernel="poly", degree=degree, C=C))

    ])

poly_kernel_svc = PolynomialKernelSVC(degree=3)

poly_kernel_svc.fit(X, y)

plot_decision_boundary(poly_kernel_svc, axis=[-1.5, 2.5, -1.0, 1.5])

plt.scatter(X[y==0,0], X[y==0,1])

plt.scatter(X[y==1,0], X[y==1,1])

plt.show()

六，什么是核函数

首先使用数学对优化函数进一步的变形：

如果使用多项式特征，x(i),x(j)变为多项式的x'(i),x'(j)再进行相乘的运算：

这样计算乘开后会复杂的多，并且增加了存储空间

核函数的想法是，可不可以不让x(i),x(j)发生上述变化，而是先对x(i),x(j)进行一个运算，使得

加入多项式特征的优化函数变为：

所以，核函数其实是一种数学技巧，并且在SVM中经常应用。

多项式核函数：

对于多项式核函数的degree,可以赋予不同的幂次：

线性核函数的d=1

七，RBF核函数

高斯核函数-SVM使用最多的核函数

高斯核函数也被称为：Radial Basis Function Kernel 镜像基函数

高斯核函数就是将每一个样本点映射到一个无穷维的特征空间

使用多项式特征为什么可以解决非线性问题？

依靠升维使得原本线性不可分的数据线性可分

方便理解：

原本的一维不可分数据长这样：

样本点都在一条直线上，就是线性不可分，但如果把样本点横坐标不变，扩充到二维空间

这样就线性可分

这就是升维的意义

高斯核的本质也是这样

在一个线性不可分的样本点中，插入俩个点l1和l2作为地标

这样y分别取这俩个地标的值，就可以变为：

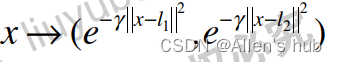
使用程序具象化高斯核函数

import numpy as np

import matplotlib.pyplot as plt

x = np.arange(-4, 5, 1)

y = np.array((x >= -2) & (x <= 2), dtype='int') #线性不可分数据

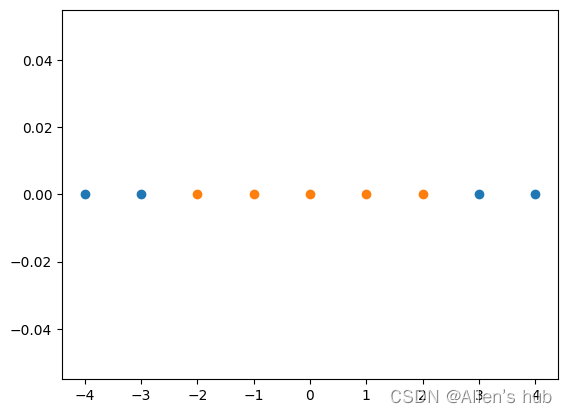
def gaussian(x, l): #定义高斯核函数 其中l表示地标

    gamma = 1.0

    return np.exp(-gamma * (x-l)**2)

l1, l2 = -1, 1 #固定地标

X_new = np.empty((len(x), 2))

for i, data in enumerate(x):

    X_new[i, 0] = gaussian(data, l1)

    X_new[i, 1] = gaussian(data, l2)

plt.scatter(X_new[y==0,0], X_new[y==0,1])

plt.scatter(X_new[y==1,0], X_new[y==1,1])

plt.show()

这样就可以线性可分了

而高斯核函数其实是把每一个数据点都作为了landmark。因此取了许多的landmark

将m*n的数据映射成为m*m的数据。所以当m<n，运算反而就会变得简单（eg.自然语言处理）

八，RBF核函数中的gamma

scikit-learn中的高斯核函数

高斯核函数：

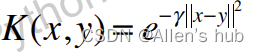
高斯函数：

图像：

gamma越大，方差越小，图像越窄，数据越集中

程序：

依旧使用半月形数据并加入相同的噪音

建立pipline

使用封装好的SVC

svc = RBFKernelSVC(gamma=1)

svc.fit(X, y)

调用边界绘制函数

plot_decision_boundary(svc, axis=[-1.5, 2.5, -1.0, 1.5])

plt.scatter(X[y==0,0], X[y==0,1])

plt.scatter(X[y==1,0], X[y==1,1])

plt.show()

svc_gamma100 = RBFKernelSVC(gamma=100)

#发现gamma越大，边界越集中，明显过拟合

svc_gamma100.fit(X, y)

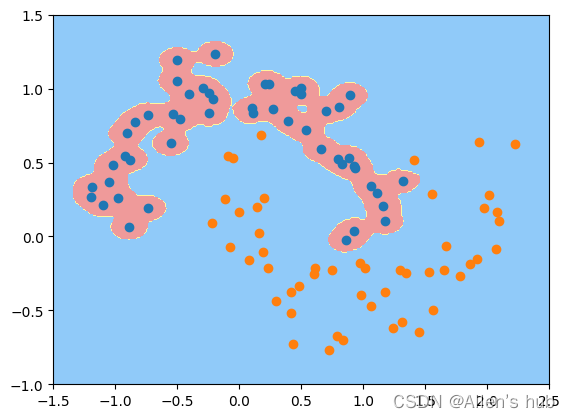
svc_gamma10 = RBFKernelSVC(gamma=10)

svc_gamma10.fit(X, y)

svc_gamma05 = RBFKernelSVC(gamma=0.5)

svc_gamma05.fit(X, y)

svc_gamma01 = RBFKernelSVC(gamma=0.1)

#gamma越小，边界越简单，会欠拟合

svc_gamma01.fit(X, y)

九，SVM思想解决回归问题

用SVM解决分类问题希望的是落在margin里的点越少越好

而用SVM解决回归问题则是希望里边的点越多越好

使用封装好的SVM

导入数据集：

import numpy as np

import matplotlib.pyplot as plt

from sklearn import datasets

from sklearn.model_selection import train_test_split

from sklearn.svm import LinearSVR #只能是线性的

from sklearn.svm import SVR #注意是不是SVC 可以有多项式

from sklearn.preprocessing import StandardScaler

from sklearn.pipeline import Pipeline

def StandardLinearSVR(epsilon=0.1): #定义pipline

    return Pipeline([

        ('std_scaler', StandardScaler()),

        ('linearSVR', LinearSVR(epsilon=epsilon))

    ])

boston = datasets.load_boston()

X = boston.data

y = boston.target

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

svr = StandardLinearSVR()

svr.fit(X_train, y_train)