二）PyTorch入门基础串讲（一）

1，机器学习中的分类与回归问题

输入变量与输出变量均为连续变量的问题称为回归问题

输出变量为有限个离散变量的预测问题是分类问题

机器学习的构成元素：

样本（特征和数量），模型，训练（获得参数），推理（计算标签），测试（评价模型）

2，Tensor与机器学习

• 采用张量描述高维的数据空间，是对标量，向量，矩阵，高维向量的一个统称。标量（矩阵或向量中每一个元素）就是零阶张量，向量是一阶张量以此类推。
• 机器学习中需要用变量来表达参数， 对于建立的模型，其参数是未知的那参数就是变量，并且，pytorch中自带了对这些变量的自动求导功能。
• nn.Module封装了搭建深度学习模型的积木元素

3，Tensor的基本定义

• 张量
• 用来描述样本和模型参数
• 可以和numpy互换
•  Tensor描述数据类型就是在数据类型前加torch.（eg: torch.float64, torch.int8）

4，Tensor的创建

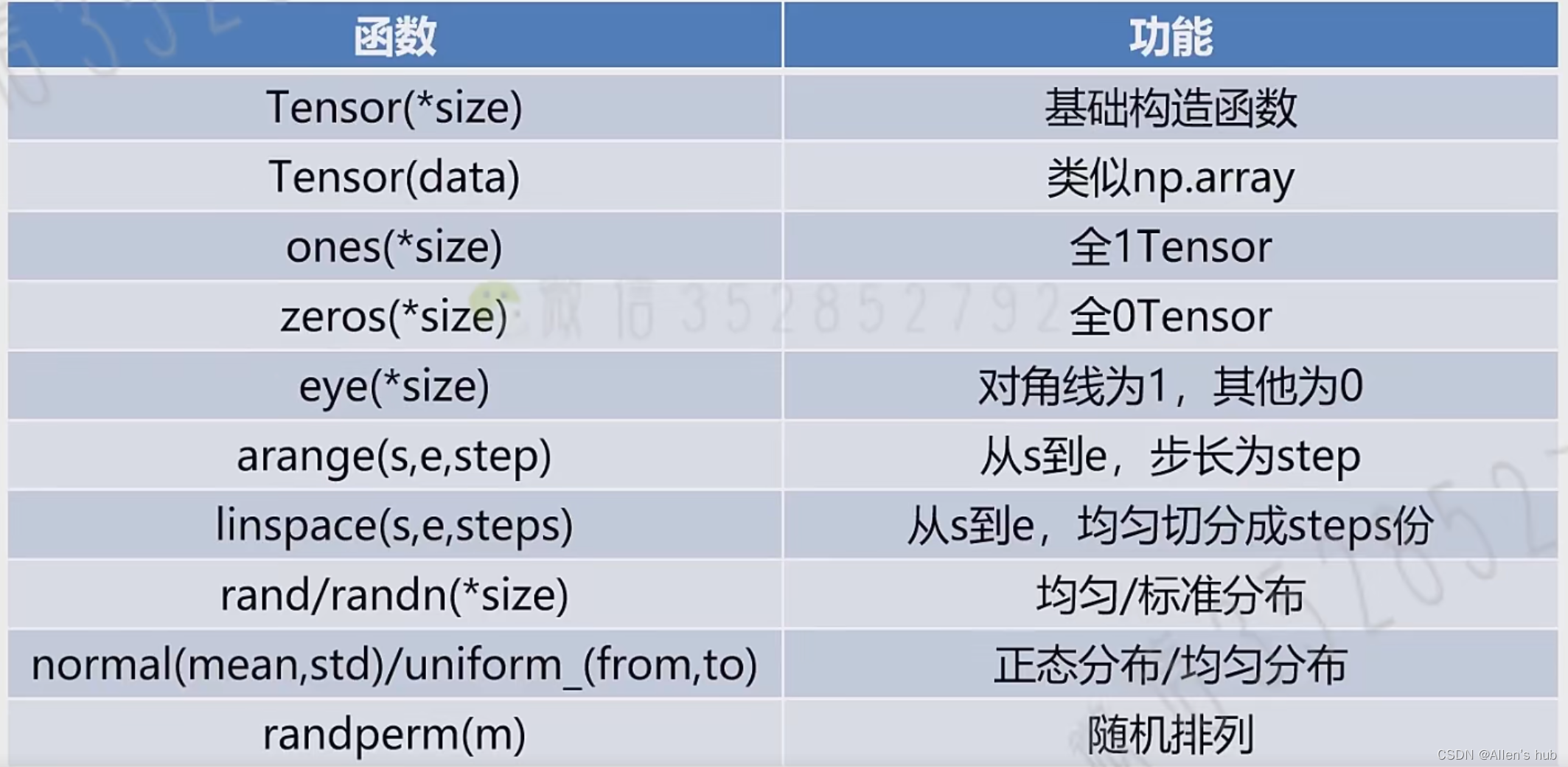
栗子：

基础构造

注意创建张量，圆括号里必须是是list，也就是最外围一定有个方括号，二维张量就是方括号套着方括号，俩层。不加方括号的话就是创建一个size的张量：

这些值都是初始化的随机的值，或者是当前内存中的值

除此之外还可以利用zeros_like或者ones_like创建与对象一样大小的张量，没有eye_like：

随机：

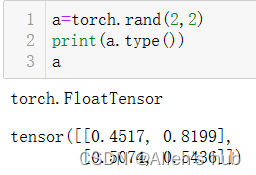
随机生成的数是在[0,1)区间。当我们看normal的源码时候会发现其中的参数均值和方差既可以是张量又可以是浮点型，当mean和std参数都是_float型时需要额外指定size参数：

这里先生成五种标准差的tensor，之后每种标准差和mean=0.0组合生成不同的正态分布的函数。之后我们就可以从这五组正态分布函数中再生成五个数。通常用于数据的初始化。

同样的是uniform均匀分布，但此时我们需要指定Tensor的大小，再去定义。

序列：

注意从0开始，步长为1，不包含10

随机序列：

与numpy对比：

功能和结构和Tensor基本是相同的，但是使用时需要互相交互，转换

5，Tensor的属性

• 每一个Tensor有torch.dtype, torch.devize, torch.layout三种属性
• torch.dtype标识数据类型
• torch.device标识了torch.Tensor对象再创建之后所存储再设备的名称，CPU, GPU
• torch.layout表示torch.Tensor内存布局的对象（数据结构中，表示稠密存储或者稀疏存储）

稠密张量：

一般不申明都是稠密张量

稀疏张量：

• 表达形式：torch.sparse_coo_tensor，其中coo类型表示了非零元素的坐标形式
• 什么是稀疏：表达了数据中非零元素的个数，0越多，数据越稀疏；在线性代数中的秩也可以表示数据的可线性表示关系，秩越小，能相互表示可能性越大。
• 通过稀疏，可以把模型变得更加简单，并且可以减小内存的开销，因此在存储稀疏的数据或模型时可以用稀疏张量进行存储，只记录非零元素的坐标。这种方法，尤其在深度学习中可以极大的减少内存消耗！

比如：

稀疏张量编程实战：

默认是在cpu上执行，cuda=0表示指定到第一张显卡里，默认也是cuda=0，那么此时的a是存放在了cuda=0上。当我们指定a的dtype，数据变成float型

默认都是稠密张量，当定义稀疏张量时，首先要定义非零元素的坐标：

数据放到GPU上，要合理的使用资源，尽可能提高迭代速率

6，Tensor的各种运算

加(add)减(sub)法运算：

注意，一切的add_(), sub_(), exp_()…这种有下划线的加减乘除等，都是直接对tensor进行操作，改变了原来的值

乘(mul)除(div)运算：

哈达玛积(element wise)是对应元素相乘，也就是点乘，因此俩个张量的大小应该相同.

矩阵乘法(mm)：

• 二维矩阵乘法运算操作包括torch.mm(),  torch.matmul(),  @

• 对于高维的Tensor (dim>2), 定义其矩阵乘法仅在最后的俩个维度上，要求前面的维度必须保持一致，就像矩阵的索引一样，并且运算操作只有torch.matmul()。

幂(pow)运算开方运算(sqrt):

幂运算：

对数(log)运算：

默认log的底数是e

取整取余：

• .floor()向下取整
• .ceil()向上取整
• .round()四舍五入
• .trunc()裁剪，只取整数部分
• .frac()裁剪，只取小数部分
• %取余

比较运算

torch.eq(input,other,out=None) #按照成员进行等式操作，相同返回True

torch.equal(tensor1, tensor2) #如果俩个tensor有相同的size和elements，返回true
torch.ge(input, other out=None) #input>=other

torch.gt(input, other out=None) #input>other

torch.le(input, other out=None) #input<=other

troch.al(input, other out=None) #input>other

torch.ne(input, other out=None) #input!=other

以上当Tensor之间比较时，返回的也是Tensor

取前k大/前k小/第k小的数值及其索引：

torch.sort(input,dim=None,descending=False,out=None) #对目标Input按照维度进行排序

注意：dim=0是对列排序，返回列的索引值；dim=1是对行的排序（numpy的axis）

理解清楚：列为轴和行为轴

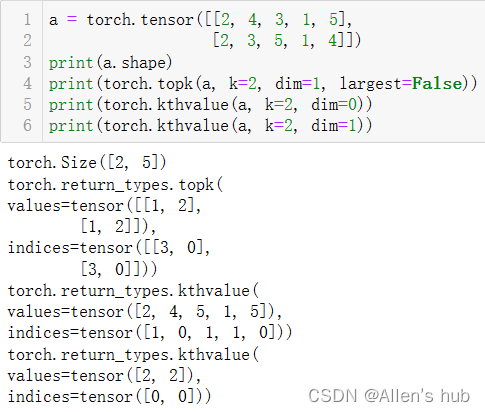
torch.topk(input, k dim=None,largest=True,sorted=True,out=None)#沿着指定维度返回最大k个数值及其索引值

torch.kthvalue(input,k,dim=None,out=None)#沿着指定维度返回第k个最小值及其索引

Tensor判断是否为finite/inf/nan

（有界/无界/是否为不是效数字）

torch.isfinite(tensor)/torch.isinf(tensor)/torch.isnan(tensor)

返回一个标记元素是否为finite/inf/nan的mask张量（布尔类型的张量）

目的是在机器学习之前对数据进行清洗

nan就是脏数据，需要去除

7，PyTorch中的in_place操作

• “就地操作”即不允许使用临时变量
• 也称为原位操作
• x=x+y
• add_, sub_, mul_等

就是会改变被操作的对象，而不是对生成的copy操作

8，PyTorch的广播机制

广播机制：张量参数可以自动扩展为相同的大小

广播机制要满足以下条件：每个张量至少一个维度，并且满足右对齐

比如：

在这里的意思就是把第一个rand中(3,2,1)右边维度1与第二个rand中的3对齐，也就是说广播后，最后一个维度小的数被广播成了与另一个矩阵一样大的数。这个例子的第一个矩阵维度变成(3,2,3)，然后让每个向量与第二个矩阵相加。

9，Tensor的函数

Tensor的三角函数：

当我们要比较俩个向量的相似性时候，可以使用欧氏距离也可以使用余弦距离

其他数学函数：

统计学相关函数：

栗子：

histc()--->>>比如灰度直方图

torch.histc(input, bins=100, min=0, max=0, *, out=None) → Tensor
如果min和max均为0，使用数据中的最小值和最大值

特征工程中经常用到灰度直方图

torch.bincount可以用来对某一样本的类别进行统计

tensor的torch.distributions

distributions包含可参数化的概率分布和采样函数

得分函数：强化学习中策略梯度方法的基础

pathwise derivate估计器：变分自动编码器中的重新参数化技巧

PyTorch中的分布函数：

• 利用KL Divergence度量俩个不同分布的相似性
• 利用Transforms  完成分布与分布的转换
• 利用Constraint对分布进行约束，再利用Transform2形成新的分布
• 对分布进行组合形成更多的分布

PyTorch中的随机抽样种子

定义随机种子：torch.manual_seed(seed)

定义随机函数满足的分布：torch.normal()（正态分布）